\(\newcommand{\V}[1]{\boldsymbol{#1}}\newcommand{\barT}[1]{\underset{#1}{\bar{T}}}\newcommand{\Tzero}{\barT{0}}\newcommand{\Ti}{\barT{1}}\newcommand{\Tii}{\barT{2}}\newcommand{\Tiii}{\barT{3}}\renewcommand{\div}{\operatorname{div}}\newcommand{\U}{\bar{U}}\renewcommand{\d}{\tilde{d}}\newcommand{\volume}{\d t \wedge \d x \wedge \d y \wedge \d z}\newcommand{\Lie}{\mathcal{L}}\)
以前、エナジー運動量テンソル \(T^{ab}\) が対称テンソルになる事情についての記事を書いたが、この度この件について再度考えてみる機会があった。その結果、以前は気づいていなかったことにいくつか気づいた。(特殊)相対性理論についてちゃんと学んだ人ならばもしかしたらよく知っている当たり前の話かもしれないが、私にとっては結構新鮮な成果であり、また他所で見たことのない話でもあるので、興味のある方向けに紹介する価値はあるだろう、と思って公開してみる。
なお、内容的には8月頃までに大体到達していた話で、以下の内容も当時8割方書き終わっていたのだが、そこで入ってきた案件に12月までこういった活動の時間を充てなくてはならなくなったため、こうやって書き上げるまでにかなり時間がかかってしまった。
取り扱う話題は、以下のようなものになる。
- \(T^{0i}=T^{i0}\) がなりたつことの意義
- 連続分布する物質の重心(質量中心)と全運動量の関係
- 熱力学第一法則 \(\Delta E = \delta Q – p\Delta V\) の、相対論での正当性。特に完全流体や平衡状態でない場合の考察。
なお、以下では、微分幾何の技法を積極的に活用する。特殊相対論に限定されているので曲率や接続は出てこず、大域的でフラットな座標系(慣性系)が存在し、異なる時空点でのベクトル(の成分)が平気で足したりできる…という点では微分幾何的には「易しい」計算しか出てこない題材なので、微分幾何の知識がある方には敷居は高くないだろう。その反面、添字の上下の使い分け、Lie 微分、微分形式とその積分、外微分といった微分幾何色の強い計算技法は遠慮なく使っていくので、微分幾何に接した機会のない方にはさっぱり計算が追えない話になってしまうと思う。これは、そうやって見通しよくすっきり計算を進められる所に意義がある話だと思うからと、あと、これを微分幾何を齧ってみるきっかけにしていただければ、という下心もちょっと働いている。「これは面白そうだ!こういう計算がすっきりできるなら、微分幾何というものを習得してみるのも悪くなさそうだ」と感じていただければ、私の目論見としては成功したことになる。私の狭い経験に限っても、微分幾何は相対論に限らず色々な場所で活用できる(電磁気、解析力学、熱力学、流体力学 etc…)ものなので、身につけて決して損にはならないはずだ。
まず、エナジー運動量テンソル \(T^{ab}\) の定義の再確認から行こう。以下の話では、「なぜエナジー運動量テンソルは対称なのか?対称であることにどんな意義があるのか?」という問題意識を持って進めていくので、定義としては2つの添字の違いを意識することになる。なお、以下ではすべて \(c=1\) の単位系を使う。
慣性系 \((t,x,y,z)=(x^{0},x^{1},x^{2},x^{3})\) を取ったとき、エナジー運動量テンソルの成分 \(T^{\mu\nu}\) は「物質の四元運動量の第 \(\mu\) 成分が、\(x^{\nu}=\text{一定}\) の面(3 次元超平面; 3-surface)を負の側から正の側に単位面積・単位時間等に通り抜ける分量」とする。もちろん \(\mu=0\) の場合は第 \(\mu\) 成分というのはエナジーを指すし、\(\nu=0\) の場合はその慣性系の\(x^{\nu}=t=\text{一定}\) の時刻での各運動量成分の密度(空間的密度)を指している。
この時、エナジー運動量保存則は、2 番目の引数に対する発散を使って
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-1}
T^{\mu\nu}_{,\nu} = 0
\end{equation}
あるいは
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-2}
T^{\mu\nu}_{,\nu} = f^{\mu}
\end{equation}
と表される。本記事では上述の通り特殊相対論(Minkowski 時空)に議論を限定するので、\(\nu\) による微分はただの偏微分でコンマ表記であり、共変微分(セミコロン表記)は出てこない(と言っても、慣性系座標ではなく球座標等の曲線座標を使うのであれば、「平坦な時空での共変微分」として扱わなければならなくなってただの偏微分ではいけなくなるのは当たり前。本記事では、そういう座標は使わず、\(\mu\), \(\nu\) 等の添字はすべて何らかの慣性系座標に付随するものとする)。
前者\eqref{eq:symmetry-of-energy-momentum-tensor2-1}は自由場の場合で、外場はなく \(T^{ab}\) は全物質のエナジー運動量を表す。一方、後者\eqref{eq:symmetry-of-energy-momentum-tensor2-2}だったら外場があり、外場から反作用 \(f^{\mu}\) によって四元運動量の供給を受けているという状況を表している。後者の場合は、\(T^{ab}\) は外場を生む物質のエナジー運動量の分は含んでいないことになる。
当面の間、慣性系 \(K\) をひとつ固定しておいて、成分は \(K\) の慣性系座標に基づくものだけ考えることにしよう。エナジー運動量保存\eqref{eq:symmetry-of-energy-momentum-tensor2-1}\eqref{eq:symmetry-of-energy-momentum-tensor2-2}をベクトルの発散として扱えるよう、次のようなベクトル場 \(\Tzero\), \(\Ti\), \(\Tii\), \(\Tiii\) を定義する。
\begin{align*}
(\Tzero)^{\mu} &= \underset{0}{T}^{\mu} = T^{0\mu} \\
(\Ti)^{\mu} &= \underset{1}{T}^{\mu} = T^{1\mu} \\
(\Tii)^{\mu} &= \underset{2}{T}^{\mu} = T^{2\mu} \\
(\Tiii)^{\mu} &= \underset{3}{T}^{\mu} = T^{3\mu}
\end{align*}
つまり、\(\barT{\mu}\) は「四元運動量の第 \(\mu\) 成分の流束」である。(私は、微分幾何はシュッツ「物理学における幾何学的方法」で学んだので、ここでは上に棒を付けることでベクトル(場)を表す、という表記を使っている。ただし \(T\) の真下に添字(的なもの)を付ける変則的な記法は同書にもなく、私がこの記事限定で使用する独自の記法である。上付きにすると普通の添字と紛らわしくなるし、普通の下付きだと微分幾何の標準的な上付き下付き記法に反してしまうし、他に適する場所もないので、仕方なくこういう記法を採っている。ローレンツ座標に対してのみしか意味を持たない添字なので、共変的な書き方に適合する必要はない)
別の言い方をすると、\(
\begin{pmatrix}
2 \\ 0
\end{pmatrix}
\) 型テンソル \(T^{ab}\) の第1引数に、座標基底 \(1\)-形式 \(\d x^{\mu}\) を代入したものが \(\barT{\mu}\) ということだ。(今 \(\d x^{\mu}\) と書いたが、外微分演算子にチルダを付けて \(\d\) と書くのも上掲書籍に沿った記法である)
この表記を用いると、エナジー運動量保存則\eqref{eq:symmetry-of-energy-momentum-tensor2-1},\eqref{eq:symmetry-of-energy-momentum-tensor2-2}は、それぞれ次のように書き表せる。
\begin{align}
\label{eq:symmetry-of-energy-momentum-tensor2-4}
\div(\barT{\mu}) &= 0 \\
\label{eq:symmetry-of-energy-momentum-tensor2-5}
\div(\barT{\mu}) &= f^{\mu}
\end{align}
時刻 \(t=x^{0}=\text{一定}\) の超平面上に適当な 3 次元領域をとり、そこで \(\Tzero\) の第 \(0\) 成分を積分すると、その領域内の全エナジーが得られる(Minkowski 時空中で、\(t=\text{一定}\) の超平面上の部分集合なので、3 次元領域が向き付け可能(従って収束さえするなら積分可能)であることは保証されているはず…)。
\[ \text{領域内エナジー} = \int_{3} \underset{0}{T}^{0} d^{3}x = \int_{3} T^{00} d^{3}x \]
この式で、\(\int_{3}\) の添字の \(3\) は、\(3\) 次元領域での積分であることを表す。\(\Tzero\) ではなく \(\Ti\) で同じことをすれば、その領域内の全運動量の \(x^{1}=x\) 成分が得られる。また、別々の時刻でのそういった積分の差を取ると、領域内のエナジー等の変化量が計れる。
\[ \varDelta E = \int_{3^{\prime}} \underset{0}{T}^{0}(t+\varDelta t) d^{3}x –
\int_{3} \underset{0}{T}^{0}(t) d^{3}x \]
ここで、3 次元領域は 2 つの時刻で共通している必要はなく、時刻 \(t + \varDelta t\) での 3 次元領域は、時刻 \(t\) での 3 次元領域とは異なる位置・形であっても構わない。時間と共に移動・変形するような 3 次元領域内のエナジーや運動量の変化を追跡したい場合は、当然そういった差を考えることになる。
\(T^{ab}\) の対称性
エナジー運動量テンソルの時間-空間成分の対称性 \(T^{0i}=T^{i0}\) がどのような意義を持つかを考察する。教科書などでは、この関係は点粒子が
\begin{align*}
E &= \frac{m}{\sqrt{1-v^{2}}} \\
\boldsymbol{p} &= \frac{m\boldsymbol{v}}{\sqrt{1-v^{2}}}
\end{align*}
の関係を持つことから「導かれる」、ということが多い。また、その議論でポイントとなるのは結局
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-3}
\boldsymbol{p} = E \boldsymbol{v}
\end{equation}
がなりたつことであるが、この形なら光子(質量 \(m=0\) の粒子)に対してもなりたつし、\(m \ne 0\) であっても \(m\) に陽にはよらない形に書けているので、文献によってはそちらをメインにして「色んな種類の粒子が交ざっている系でも各粒子がそれぞれ\eqref{eq:symmetry-of-energy-momentum-tensor2-3}をみたすので \(T^{0i}=T^{i0}\) がなりたつ」という説明をしていることもあるだろう。ただ、いずれの説明でもすべての粒子が相互作用なしで自由粒子として飛び交っている、という状況(ダスト)を暗黙のうちに仮定していることになり、粒子同士のポテンシャルエナジーや圧力や粘性、熱伝導があるような複雑な系でまで \(T^{0i}=T^{i0}\) と言える根拠になっているかどうかはやや疑わしい所がある。ここでは、別の観点から「\(T^{0i}=T^{i0}\) がなりたっていることはどういう帰結をもたらすか」を考え、その帰結に基づき考察を行う。
まずは、自由場の場合\eqref{eq:symmetry-of-energy-momentum-tensor2-1}から考える。エナジーと、運動量の各成分についての 4 つの保存則\eqref{eq:symmetry-of-energy-momentum-tensor2-4}がなりたっているが、このうちまずエナジー保存 \(\div(\Tzero)=0\) について考える。これは、「(\(K\) で観測される)エナジーが、時空中を \(\Tzero\) というベクトル場に沿って流れている」という見方ができる。したがって、3 次元的な領域をこのベクトル場に従って時刻と共に移動・変形させていけば、その中に含まれるエナジー総量は不変であると考えられる。これは実際、次のようにして確認できる。
まず、適当な時刻 \(x^{0}=t=\text{一定}\) の超平面上に、境界付き 3 次元領域をひとつ取り固定する。次に、その 3 次元領域(の各点)を、ベクトル場 \(\Tzero\) に従って動かす。得られたチューブ状の 4 次元領域の、別の時刻 \(x^{0}=\text{一定}\) での断面を考える。この操作がうまく行くよう、考えている領域では \(\Tzero\) は常に因果的(つまり時間的かヌルかのどちらか)ベクトルであるとしよう(現実的な物質のエナジー運動量テンソル \(T^{ab}\) から作られる \(\Tzero\) では、この仮定は真空ではない時空点(\(T^{ab} \ne 0\) の時空点)では常になりたつ。大抵の場合は時間的ベクトルになるが、電磁気の \(T^{ab}\) のように、状況によってはヌルベクトルになるものもある)。この仮定のもとでは、\(\Tzero\) に沿って \(x^{0}\) は常に変化し続けるので、上の想定のように別の時刻 \(x^{0}=t+\varDelta t = \text{一定}\) 超平面と必ず交わり、元の 3 次元領域のすべての点について「その時刻でどの位置に移ったか」がちゃんと決まる。
こうすると、2 つの時刻での 3 次元領域が 4 次元チューブ領域の「底面」と「上面」になっており、元の 3 次元領域の境界の 2 次元面が \(\Tzero\) に沿って移動した軌跡が 4 次元チューブ領域の「側面」をなしている。これらの面で囲まれた4 次元チューブ領域で
\[ \div(\Tzero) = 0 \]
の両辺を積分すると、左辺は \(\Tzero\) の表面積分となり、
\[ E(t+\varDelta t) – E(t) + \int_{\text{側面}} \Tzero = 0 \]
となる。ところが、上述の通り側面は \(\Tzero\) が接するような \(3\) 次元面だから、この側面に関する表面積分は \(0\) になる。したがって \(E(t+\varDelta t) = E(t)\) となり、\(\Tzero\) に沿って \(E\) は一定である。
以上で、次の定理が示された。
\(\div(\Tzero)=0\) とする。\(t=\text{一定}\) 超平面上の 3 次元領域内の全エナジー
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-6}
E = \int_{3} T^{00} d^{3}x
\end{equation}
は、3 次元領域をベクトル場 \(\Tzero\) に沿って移動しても不変(時刻によらない一定値)である(ただし、\(\Tzero\) は因果的ベクトルとする)。
同じことを、積分形ではなく微分形でも見ておこう。これは、次の話の準備も兼ねている。時刻 \(x^{0}=t+\varDelta t\) と \(x^{0}=t\) のエナジーの差を微分として捉えよう。ベクトル場の積分曲線に沿っての積分値の変化を見るのだから、基本的には Lie 微分で表すことになるが、ちょっと注意が必要なのは、\(\Tzero\) による Lie 微分ではうまく行かないということだ。ここでは、2 つの \(x^{0}=\text{一定}\) 面で積分値の差を見るわけだから、「\(x^{0}\) を微分したときに \(1\) になる」ようなベクトル場での Lie 微分を考えなければいけない。つまり、\(\Tzero\) をスケール変換して、\(\U(x^{0})=1\) となるようなベクトル場 \(\U\) を作り、その \(\U\) による Lie 微分を考えなければいけない。
簡単な計算から、\(\U\) は \(\Tzero\) から次の関係によって決まるベクトル場となる。
\[ \Tzero = T^{00} \U \]
(この定義についてちょっと補足。上で行った \(\Tzero\) についての仮定から、今考えている領域では \(T^{00} \ne 0\) である。よって \(\U\) は問題なく定義される。また、\(U^{0}=1\) なので \(\U\) は相対論でよく出てくる四元速度ベクトルではない)単にスケール変換しているだけだから、\(\U\) の積分曲線と \(\Tzero\) の積分曲線は一致している。この積分曲線に沿って動かされる(Lie 移動される)3 次元領域の、各時刻 \(x^{0}=t\) での総エナジー\eqref{eq:symmetry-of-energy-momentum-tensor2-6}を \(t\) の関数として捉えようとしているわけだ。それを \(t\) で微分したものを Lie 微分ですっきり計算するために、(超)体積 \(4\)-形式
\[ \volume \]
を導入する。これを使うと
\begin{align*}
T^{00} d^{3}x &= (\Tzero)^{0} \d x \wedge \d y \wedge \d z \\
&= (\volume)(\Tzero) \Bigr\rvert_{t}
\end{align*}
と書ける(最終項は、\(3\)-形式 \((\volume)(\Tzero)\) の \(t=\text{一定}\) 超平面への制限を表す)ので、\eqref{eq:symmetry-of-energy-momentum-tensor2-6}が \(t=\text{一定}\) 超平面の一部に対する積分であることを考えると
\begin{align*}
\eqref{eq:symmetry-of-energy-momentum-tensor2-6} &=
\int_{3} (\volume)(\Tzero) \\
\therefore \frac{d}{dt} \int_{3} T^{00} d^{3}x &= \int_{3} \Lie_{\U}
\bigl\{ (\volume)(\Tzero) \bigr\}
\end{align*}
である。ここで、\(\Lie_{\U}\) は Lie 微分を表す。右辺の被積分関数(被積分形式)を、形式の Lie 微分を外微分のみで表す式
\[ \Lie_{\bar{V}} \tilde{\alpha} = (\d \tilde{\alpha})(\bar{V}) + \d(\tilde{\alpha}(\bar{V})) \]
を使って計算すると
\begin{align*}
\Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} &= \bigl\{\d \bigl((\volume)(\Tzero)\bigr) \bigr\}(\U) + \d ((\volume)(\Tzero, \U)) \\
&= \underbrace{\div(\Tzero)}_{0 (\because \eqref{eq:symmetry-of-energy-momentum-tensor2-4})}(\volume)(\U) +
\d ((\volume)(T^{00}\U, \U)) \\
&= \d (T^{00}\underbrace{(\volume)(\U, \U)}_{0}) \\
&= 0
\end{align*}
となる(1行目から2行目にかけては、div の定義
\[ \div(\bar{V}) (\underbrace{\volume}_{\text{(超)体積$n$-形式}}) = \d \bigl((\underbrace{\volume}_{\text{(超)体積$n$-形式}})(\bar{V})\bigr) \]
を使った)。よって
\[ \frac{d}{dt} \int_{3} T^{00} d^{3}x = 0 \]
である。
さて、まだ \(T^{0i}=T^{i0}\) の話に入っていないが、その前にもうひとつ準備の話を行う。Newton 力学では「全運動量が重心(質量中心)の速度と全質量の積になる」という関係は、連続的な質量分布がある際でも正しかった。つまり、\(\rho\) を質量密度として
\begin{align*}
\boldsymbol{P} &= M \frac{d}{dt} \boldsymbol{R} \\
M &= \int \rho d^{3}x \\
\boldsymbol{R} &= \frac{1}{M} \int \rho \boldsymbol{r} d^{3}x
\end{align*}
である。Newton 力学では全質量 \(M\) は保存するので、結局
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-7}
\boldsymbol{P} = \frac{d}{dt} \int \rho \boldsymbol{r} d^{3}x
\end{equation}
ということになる。これに相当する式が(特殊)相対論ではどうなるか見てみよう。
引き続き \(\U\) は \(\Tzero = T^{00}\U\) で定まるベクトル場とし、\(\U\) に沿って移動させた 3 次元領域について、\(\int T^{00} x^{i} d^{3}x\) を微分してみたらどうなるかを考えてみる。つまり、相対論で\eqref{eq:symmetry-of-energy-momentum-tensor2-7}の右辺に相当するものを計算してみるわけだ。\(i=1,2,3\) のどれに対しても本質的には同じことになるので、以下では \(i=1\) としてみる。先ほどと同様に
\begin{align*}
T^{00} x^{1} d^{3}x &= x (\Tzero)^{0} \d x \wedge \d y \wedge \d z \\
&= x (\volume)(\Tzero) \Bigr\rvert_{t}
\end{align*}
であるから
\begin{align}
\int_{3} T^{00} x^{1} d^{3}x &= \int_{3} x (\volume)(\Tzero) \notag\\
\label{eq:symmetry-of-energy-momentum-tensor2-9}
\therefore \frac{d}{dt} \int_{3} T^{00} x^{1} d^{3}x &= \int_{3}
\Lie_{\U} (x (\volume)(\Tzero))
\end{align}
となる。ここで、
\begin{align*}
\Lie_{\U} (x (\volume)(\Tzero)) &= (\Lie_{\U} x) (\volume)(\Tzero) + x \underbrace{\Lie_{\U} \bigl\{(\volume)(\Tzero)\bigr\}}_{\div(\Tzero)=0\text{のもとで\(0\)だった}} \\
&= U^{1} (\volume)(\Tzero) \\
\therefore \Lie_{\U} (x (\volume)(\Tzero)) \Bigr\rvert_{t} &= U^{1} (\volume)(\Tzero) \Bigr\rvert_{t} \\
&= U^{1} (\Tzero)^{0} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} \\
&= \underbrace{U^{1} T^{00}}_{(\Tzero)^{1} (\because \Tzero = T^{00}\U)} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} \\
&= T^{01} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t}
\end{align*}
なので、\eqref{eq:symmetry-of-energy-momentum-tensor2-9}と合わせると
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-10}
\frac{d}{dt} \int_{3} T^{00} x^{1} d^{3}x = \int_{3} T^{01} \d x \wedge \d y \wedge \d z
\end{equation}
がなりたつ。
一方、\eqref{eq:symmetry-of-energy-momentum-tensor2-7}の左辺の \(x\) 成分に当たるものは、相対論では
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-11}
\int_{3} \underbrace{T^{10}}_{\text{運動量の\(x\)成分の密度}} d^{3}x = \int_{3} T^{10} \d x \wedge \d y \wedge \d z
\end{equation}
である。
\eqref{eq:symmetry-of-energy-momentum-tensor2-10}と\eqref{eq:symmetry-of-energy-momentum-tensor2-11}の右辺は、\(T^{01}=T^{10}\) ならば一致する。つまり、エナジー運動量テンソルで \(T^{0i}=T^{i0}\) がなりたつことは、「相対論でも\eqref{eq:symmetry-of-energy-momentum-tensor2-7}に相当する式
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-12}
\int_{3} T^{10} d^{3}x = \frac{d}{dt} \int_{3} T^{00} x^{1} d^{3}x
\end{equation}
がなりたつ」ということを意味するのだ!
ここで、上で示した通り「\(\div(\Tzero)=0\) なら全エナジー \(E=\int_{3} T^{00} d^{3}x\) は \(\U\) に沿って保存する」ことを思い出そう。これは Newton 力学で全質量 \(M=\int \rho d^{3}x\) が保存することに対応するが、これによって
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-13}
\frac{d}{dt} \int_{3} T^{00} x^{1} d^{3}x = E \frac{d}{dt}
\frac{\int_{3} T^{00} x^{1} d^{3}x}{E}
\end{equation}
が言える。したがって、相対論でも、観測する慣性系 \(K\) を固定した上で、重心(質量中心改めエナジー中心)\((X^{1}, X^{2}, X^{3})\) を
\[ X^{i} = \frac{1}{E} \int_{3} T^{00} x^{i} d^{3}x \]
によって定義すれば、\eqref{eq:symmetry-of-energy-momentum-tensor2-12},\eqref{eq:symmetry-of-energy-momentum-tensor2-13}によって
\[ \int_{3} T^{10} d^{3}x = E \frac{dX^{1}}{dt} \]
すなわち
\[ \underbrace{\boldsymbol{P}}_{\text{全運動量}} = \underbrace{E}_{\text{全エナジー}} \underbrace{\boldsymbol{V}}_{\text{重心の速度}} \]
がなりたつということになる。相対論での質点に対する関係式\eqref{eq:symmetry-of-energy-momentum-tensor2-3}と同じ形の等式が、連続的な物質分布でも成立するということだ。
次に、外場があって\eqref{eq:symmetry-of-energy-momentum-tensor2-5}となる場合を考えてみよう。この場合、\(T^{ab}\) には「外場を発生させる物質(場)」の寄与は含まれておらず、「着目している物質種のエナジー・運動量」しか含まれない。したがって、そこから作った \(\Tzero\) 及び \(\U\) は「着目している物質種のみのエナジー流束」や「それに基づく時間微分演算子」になっている。(つまり、着目している領域では、「外場に由来するエナジー流束」等が \(\Tzero\) や \(\U\) とは別個に存在(共存)している)
このときは
\begin{align*}
\Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} &= \bigl\{ \d((\volume)(\Tzero)) \bigr\}(\U) + \d \bigl\{
\underbrace{(\volume)(\Tzero, \U)}_{0 (\because \Tzero = T^{00} \U)} \bigr\} \\
&= (\div(\Tzero)) (\volume)(\U) \\
&= f^{0} (\volume)(\U) \\
\therefore \Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} \Bigr\rvert_{t} &= f^{0} U^{0} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} \\
&= f^{0} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t}
\end{align*}
なので
\begin{align*}
\frac{dE}{dt} &= \frac{d}{dt} \int_{3} T^{00} d^{3}x \\
&= \frac{d}{dt} \int_{3} (\volume)(\Tzero) \\
&= \int_{3} \Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} \\
&= \int_{3} f^{0} \d x \wedge \d y \wedge \d z
\end{align*}
となる。つまり、\(\U\) に沿って移動する 3 次元領域を考えると、全エナジー \(E\) は(当然)保存せず、外場によって単位体積・単位時間当たり \(f^{0}\) のエナジーが供給される、ということになる。
さらに
\begin{align}
\Lie_{\U} \bigl\{ x(\volume)(\Tzero) \bigr\} &= (\Lie_{\U} x) (\volume)(\Tzero) + x \Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} \notag\\
&= U^{1} (\volume)(\Tzero) + x f^{0}(\volume)(\U) \notag\\
\therefore \Lie_{\U} \bigl\{ x(\volume)(\Tzero) \bigr\} \Bigr\rvert_{t} &= U^{1} (\volume)(\Tzero) \Bigr\rvert_{t} + x f^{0} (\volume)(\U) \Bigr\rvert_{t} \notag\\
&= U^{1}T^{00} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} + xf^{0} U^{0} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} \notag\\
&= T^{01} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} + xf^{0} \d x \wedge \d y \wedge \d z \Bigr\rvert_{t} \notag\\
\therefore \frac{d}{dt} \int_{3} T^{00} x^{1} d^{3}x &= \int_{3} \Lie_{\U} \bigl\{ x(\volume)(\Tzero) \bigr\} \notag\\
\label{eq:symmetry-of-energy-momentum-tensor2-14}
&= \int_{3} T^{01} d^{3}x + \int_{3} x f^{0} d^{3}x
\end{align}
となる。やはり \(T^{0i}=T^{i0}\) がなりたつと仮定すれば、質点の力学で\eqref{eq:symmetry-of-energy-momentum-tensor2-14}に相当する話は、「仕事を受けていて \(E \ne \text{一定}\) の場合には \(\boldsymbol{p} = \frac{d}{dt}(E \boldsymbol{r})\) はなりたたずに
\[ \frac{d}{dt} (E \boldsymbol{r}) = \underbrace{E \boldsymbol{v}}_{\boldsymbol{p}} + \dot{E} \boldsymbol{r} \]
となる」ということである(\eqref{eq:symmetry-of-energy-momentum-tensor2-14}最終項の \(f^{0}d^{3}x\) が、その微小体積での \(\dot{E}\) に相当することに注意)。
熱力学第1法則と相対論での圧力
ここまでは、時間微分の演算子 \(\U\) は \(\Tzero\) に平行なものを考えてきた。ここからは、そうとは限らない場合に話を拡張しよう。
容器の中に気体や液体が封入されていて、その容器が変形して容積が変わる…という熱力学的な状況を、これまで見てきたような枠組の中で扱うことを考えよう。このような場合、気体や液体が分布する 3 次元的領域は 2 次元的な境界を表面として持ち、「全エナジー」等はその容器内の積分として捉えるべきものになる。すると、時空中でその 3 次元領域の移動を表すベクトル場 \(\U\) は、実際の容器の 2 次元境界面の軌跡に沿って定義されるべきことになり(この条件からは、\(\U\) の積分曲線は 3 次元領域の内部の点についてはあいまいにしか定まらない。「内部」が境界を突き抜けて「外部」に行くことはない、という程度の制限しかなく、ベクトル場 \(\U\) に対しては不定性が残る)、必ずしも \(\Tzero = T^{00}\U\) をみたすとは限らなくなるはずだ。そこで、以下では \(\U\) は \(\U^{0}=1\) 以外の条件は特に課さずに考える(※ もちろん、連続性や滑らかさ等は必要なだけ十分に持っているとする)。時空中では 3 次元領域はこの \(\U\) に沿って動くと考える。2 次元境界の動きも当然 \(\U\) に沿っている(上述の通り、境界での \(\U\) は境界の動きに合わせて定義したので当たり前)。
熱平衡にある場合、あるいは容器の変形が熱力学的な意味で準静的と見なせる場合には、熱力学の知識から、大まかには
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-8}
\Delta E = \delta Q -p\Delta V
\end{equation}
の変化が起きるはずだが、今考えている相対論的な状況で\eqref{eq:symmetry-of-energy-momentum-tensor2-8}に当たる式がどのような形になるか(どの程度再現されるか)を考えてみよう。
まず予備的な考察として、\eqref{eq:symmetry-of-energy-momentum-tensor2-8}はそのままではなりたたないはずだ、ということはすぐわかる。容器の変形を前提としているので 3 次元領域が外力を受ける状況を想定しているが、そうすると仮に初期状態で容器と内部の連続体が静止していたとしても、外力によって全体が並進運動量を持つことがありうる。仮に断熱壁で囲まれた容器を変形しないで加速した場合、\eqref{eq:symmetry-of-energy-momentum-tensor2-8}の右辺は \(0\) になる一方、全エナジー \(E\) は全体の運動エナジーも含んでいるので、左辺は正の値となってしまう。改めて\eqref{eq:symmetry-of-energy-momentum-tensor2-8}がどんな式だったかを反省してみると、熱力学の議論では、\eqref{eq:symmetry-of-energy-momentum-tensor2-8}を含むほとんどの場合は、変化の前後で「容器+内部流体」の全体は観察している慣性系で静止しているという暗黙の仮定があることに気づく。そもそも、Newton 力学の段階ですら「系の全エナジー」というものは慣性系によって異なる値を持つ(重心の速度は慣性系依存)ものだったのだから、\eqref{eq:symmetry-of-energy-momentum-tensor2-8}は特定の慣性系を暗黙のうちに仮定したものだったわけで、相対論にこの話を持っていくにはまず「どの慣性系を使うべきか」を特定するなり、慣性系の選び方によらない形に一般化するなりしないといけない…ということがわかる。その辺りの詳しいことは詳しく調べないとわからないので、予備考察はこのくらいで打ち切り、具体的な計算に入る。
\(t=\text{一定}\) の超平面上に 3 次元領域を取る。この領域は 2 次元境界によって「内側」と「外側」に分けられるとする。必要に応じて、領域や境界に「連結」や「単連結」などの性質は適宜仮定してよいとしよう。仮定から、3 次元領域・2 次元境界とも向き付け可能と言える、はず…。上述の通り、\(\U\) は \(U^{0}=1\) となるような適当なベクトル場とし、\(\U\) によって 3 次元領域を Lie 移動して任意の時刻での 3 次元領域およびその境界を作っておく。
3 次元領域内の全エナジーを \(E\) とし、\(\U\) に沿っての \(E\) の変化を考える。上の方の計算で、\(\Tzero \ne T^{00}\U\) でも成立する部分を再利用するとこうなる。
\begin{align*}
E &= \int_{3} T^{00} d^{3}x = \int_{3} (\volume)(\Tzero) \\
\frac{dE}{dt} &= \int_{3} \Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} \\
\Lie_{\U} \bigl\{ (\volume)(\Tzero) \bigr\} &= \div(\Tzero)(\volume)(\U) + \d ((\volume)(\Tzero, \U)) \\
\therefore \frac{dE}{dt} &= \int_{3} f^{0} \d x \wedge \d y\wedge \d z + \int_{3} \d ((\volume)(\Tzero, \U)) \\
&= \int_{3} f^{0} d^{3}x + \int_{2} (\volume)(\Tzero, \U)
\end{align*}
ここで、最後の項は、3 次元領域の境界の 2 次元面での面積分になっている。この第 1 項は既に出てきた「外場が供給する、単位体積・単位時間あたりのエナジー」の総和だ。これはジュール熱のようなものだから想像しやすい。普通は熱力学的関係の\eqref{eq:symmetry-of-energy-momentum-tensor2-8}ではそのようなエナジー収支は考えに入れないが、それは議論を簡単にするためであって、実際にジュール熱のような形で系にエナジーが供給される時はその寄与は\eqref{eq:symmetry-of-energy-momentum-tensor2-8}では \(\delta Q\) に組み入れるべきものだろう。つまり第 1 項 \(\int_{3} f^{0} d^{3}x\) は \(\delta Q\) の一部になる。問題は第 2 項
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-15}
\int_{2} (\volume)(\Tzero, \U)
\end{equation}
だ。ここが、\(\Tzero \ne T^{00}\U\) によって新たに現れるようになった項だ。
今、表面積分している 2 次元領域は \(t=\text{一定}\) 超平面上にあるので、\eqref{eq:symmetry-of-energy-momentum-tensor2-15}の被積分形式は \(t=\text{一定}\) に制限してよい。
\begin{align*}
(\volume)(\Tzero, \U) \Bigr\rvert_{t} &=
(\Tzero)^{0}(\d x \wedge \d y\wedge \d z)(\U) \Bigr\rvert_{t} – U^{0}(\d x \wedge \d y\wedge \d z)(\Tzero) \Bigr\rvert_{t} \\
&= (\d x \wedge \d y\wedge \d z)(T^{00}\U – \Tzero) \Bigr\rvert_{t}
\end{align*}
ここに現れているベクトル \(T^{00}\U – \Tzero\) は時間成分が \(0\) で、純空間的ベクトルだ。これを普通の 3 次元ユークリッド空間と同様に、表面積分すればいい。それで\eqref{eq:symmetry-of-energy-momentum-tensor2-8}の \(-p\Delta V\) に相当する項が出てくるはず………!
………と思いたい所だが、何かがおかしい。\(T^{00}\U – \Tzero\) の空間成分に現れる \(T^{ab}\) の成分は \(T^{00}\) と \(T^{0i}\) だけだ。つまり 時間-時間 成分と 時間-空間成分である。一方、圧力 \(p\) というのは明らかに \(T^{ab}\) の 空間-空間 成分だったはずだ。とすると、\(T^{00}\U – \Tzero\) からどうやって圧力 \(p\) を含む \(-p\Delta V\) みたいな項が出てくることがあるのだろうか?
様子を探るために、よく使われる単純化された例、完全流体のエナジー運動量テンソル
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-16}
T^{ab}=\rho w^{a}w^{b} + p(w^{a}w^{b}+g^{ab})
\end{equation}
ではどうなっていたかを確認してみよう。ここで、\(w^{a}\) は流体要素の四元速度ベクトルである(\(w^{a}\) ではなく \(u^{a}\) と書かれることが多いが、それだとここで扱っている \(\U\) と紛らわしいので \(w^{a}\) にした)。この場合、時間-空間成分は \(T^{01} = (\rho + p)w^{0}w^{1}\) となるので、確かに圧力 \(p\) が顔を出している。これは一体どういうことなのか。
改めて考えてみると、完全流体\eqref{eq:symmetry-of-energy-momentum-tensor2-16}で圧力 \(p\) が 空間-空間 成分として現れると言っているときは、\(w^{a}\) が「(3 次元)速度 \(0\)」に見えるような(局所)慣性系 \(K’\) で考えていることがわかる。これが、今観測に使っている固定された慣性系 \(K\) と異なっていることが「\(K\) での 時間-空間 成分\(T^{01}\)」に、「\(K’\) での 空間-空間 成分 \(p\)」が顔を出す理由だ。つまり背景にあるのは Lorentz 変換であり、Lorentz 変換による成分の入り交じりによって、\(T^{01}\) に圧力 \(p\) が含まれるようになるのだ。
また、この考察から、次のこともわかる。「何も考えずに、ただ \(T^{ab}\) の 空間-空間 成分を取っただけでは、我々が「圧力」と呼んでいるものは出てこない。「圧力」と呼ばれるものは、何らかの基準に基づいた慣性系を選び出し、その慣性系のもとでの \(T^{ab}\) の 空間-空間 成分を取って初めて得られる」のだ(圧力を「応力」に一般化しても同様)。
今考えたいのは、3 次元領域の境界の「壁」に、「圧力」によってはたらく力だ。「壁」、つまり 2 次元表面は \(\U\) に従って時空中を動いている。したがって、「圧力」を始めとする応力は、「この \(\U\) が『速度 \(0\)』に見えるような局所慣性系のもとでの \(T^{ab}\) の成分」として定義されるはずだ。もともと「圧力」というのは「単位時間、単位体積あたりに、『壁』を通して向こう側へ送り込まれる運動量(の壁に垂直な方向の成分)」を表しているわけだが、その「壁」が動いてしまっていると「『壁』を通して向こう側へ送り込まれる」分をどうやって算定すべきかに曖昧さが生じてしまう、ということが話をややこしくしている元凶だ。というのは、この『壁』というのは、必ずしも実体を持った非透過性のものとは限らず、宇宙空間中を漂う薄いガスの中に想定した「単なる想像上の境界面」ということもありうるし、また普通の物質を通さないようなガチガチの固い壁であっても、\(T^{ab}\) として考えている物質場がニュートリノのようなものだったら、どんな壁でも事実上「想像上の壁」と何ら変わらない影響しか持たないだろう。そういった透過性の壁で考えると、壁の位置が(慣性系 \(K\) で)変化するだけで、「その壁を通って反対側に移る」ような(四元)運動量が自然に発生してしまう。「圧力」(や「応力」)を考えるときは、そういった壁の位置の変化があるときは、それによって当然発生する分を除いた、「正味の」運動量移行分に基づいて考えたいわけである。それを自然に実現するために、一時的に「壁の速度が \(0\) に見える局所慣性系」の力を借りることになるわけだ。
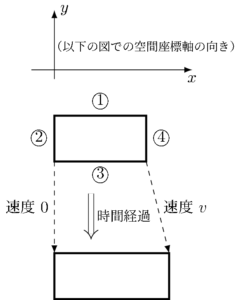
以上の考察をもとに、先ほどの計算の続きに戻ろう。簡単のため、熱力学で気体がピストンを押して体積を増やすときのように、3 次元領域が図のように \(x\) 軸方向に伸びた筒のような形で、その「右端」が動く場合を考える。
\(\U\) は 3 次元領域の各点、特にその表面の 2 次元境界の移動を表している。図で、マル1, マル2, マル3 の境界は動いていないので、これらの境界上では \(\U\) は時間成分 \(U^{0}=1\) だけ持ち、空間成分は \(0\) としてよい。マル4 は境界が右に速度 \(v\) で進んでいるとしよう。すると、マル4上では \(U^{1}=v\), \(U^{2}=U^{3}=0\) になる。「ピストン」の速度は時間的に一定でなくてもよいので、\(v\) は着目している特定の時刻での速度だとしよう。ただし、「ピストン」は平面を保ったまま進んでいくとし、マル4上では \(v\) の値の空間的な変化はないとする。
\eqref{eq:symmetry-of-energy-momentum-tensor2-15}はこんな式だった。
\[ \int_{2} (\volume)(\Tzero, \U) \]
この 2 次元表面積分の、マル1〜マル4のそれぞれからの寄与を評価しよう。マル1は \(y=\text{一定}\) の面で、「外向き」が \(y\) の正の向きだから、マル1では被積分形式は
\begin{align*}
(\volume)(\Tzero, \U) \Bigr\rvert_{t,y} &= -U^{0}(\Tzero)^{2} \d z \wedge
\d x \Bigr\rvert_{t,y} \\
&= -T^{02} \d z \wedge \d x \Bigr\rvert_{t,y}
\end{align*}
となる。「\(y=\text{一定}\) の平面を、負の側から正の側に単位面積・単位時間あたりに抜けていくエナジー」(の \(-1\) 倍)になるべくしてなっていて、これを面マル1で積分して微小時間 \(\varDelta t\) をかければ、「\(\Delta t\) の間の『内部』のエナジーの変化(減少)の、面マル1からの寄与」という当たり前の量になる。上述のようにこの面マル1は必ずしも不透過性の壁とは限らないので、この \(T^{02}\) は「仮想上の壁を、着目物質が通り抜けることによるエナジー流束」かもしれないし、「着目物質は通り抜けられないが、熱の形でエナジーが抜けて行ってる」のかもしれない。どちらなのかは、エナジー運動量テンソル \(T^{ab}\) の(成分の)値だけではわからない(区別されない)。その識別を行う必要がある場合は、物質場(生の \(\phi\) 等)のマル1(付近)でのもっと詳しい値が必要になるわけだ。壁が半透過性の場合は、その両方の合計になる。このようにして、\eqref{eq:symmetry-of-energy-momentum-tensor2-8}のマル1からの寄与は、\(\delta Q\) や、\eqref{eq:symmetry-of-energy-momentum-tensor2-8} に現れていない「物質量そのものの増減(出入り)」に付随するものになる。
続いてマル2を考える。これは \(x=\text{一定}\) の面だが、「外向き」が \(x\) の負の向きである。よって、マル2では被積分形式は負号がひとつ追加されて
\begin{align*}
(\volume)(\Tzero, \U) \Bigr\rvert_{t,x} &= -(-U^{0})(\Tzero)^{1} \d y \wedge
\d z \Bigr\rvert_{t,x} \\
&= T^{01} \d y \wedge \d z \Bigr\rvert_{t,x}
\end{align*}
のようになる。これも、「\(x=\text{一定}\) の平面を、負の側から正の側に単位面積・単位時間あたりに入ってくるエナジー」を正しく捉えている。着目物質の移動による輸送なのか、熱が伝わっているのかは区別されないことはマル1と同じだ。
マル3も同様で、特に新しいことはないので省略する。問題はマル4だ。先ほどの考察から、マル4に関する積分は、マル4での \(\U\) が「速度 \(0\)」に見えるような局所慣性系 \(K’\) を取って計算するべきだ、ということになる。すると \(K’\) は \(K\) から見て \(x\) 方向に速度 \(v\) で進んでいるわけだから、\(K’\) の慣性座標 \((t’, x’, y’, z’)\) に対する Lorentz 変換はいつも通り次の式になる(原点を合わせる必要はないので、各々の式には定数項がついていても構わない。以下の計算には影響しない)。
\begin{align*}
t’ &= \frac{t-vx}{\sqrt{1-v^{2}}} & y’ &= y \\
x’ &= \frac{x-vt}{\sqrt{1-v^{2}}} & z’ &= z
\end{align*}
そこで、\(K’\) では \(\U\) が空間成分を持たないことに注意すると
\begin{align}
\d t’ \wedge \d x’ \wedge \d y’ \wedge \d z’ &= \volume \notag\\
\therefore (\volume)(\Tzero, \U) \Bigr\rvert_{t’,x’} &=
(\d t’ \wedge \d x’ \wedge \d y’ \wedge \d z’)(\Tzero, \U) \Bigr\rvert_{t’,x’}
\notag\\
&= -U^{0^{\prime}}(\Tzero)^{1^{\prime}} \d y’\wedge \d z’ \Bigr\rvert_{t’,x’} \notag\\
\label{eq:symmetry-of-energy-momentum-tensor2-17}
&= -U^{0^{\prime}}T^{01^{\prime}} \d y\wedge \d z \Bigr\rvert_{t’,x’}
\end{align}
となる。最後の式では、\(T^{ab}\) の添字がダッシュ付きのものとそうでないものが交じっていることに注意しよう。
Lorentz 変換式、あるいは \(\U\) のノルムが慣性系不変であることを利用すると、\(U^{0′}\) の値は \(U^{0′}=\sqrt{1-v^{2}}\) とわかる。そして再度先ほどの考察を思い返せば「エナジー運動量テンソルの成分は、\(K’\) のものを主役にする」べきだから、\(T^{01′}\) のダッシュなし添字 \(0\) の方に Lorentz 変換を適用すべきとわかり、
\begin{align*}
T^{01′} &= T^{\mu’1′} \frac{\partial x^{0}}{\partial x^{\mu’}} \\
&= T^{0’1′} \times \frac{\partial t}{\partial t’} + T^{1’1′} \times
\frac{\partial t}{\partial x’}\\
&= T^{0’1′} \frac{1}{\sqrt{1-v^{2}}} + T^{1’1′} \frac{v}{\sqrt{1-v^{2}}} \\
&= \frac{T^{0’1′} + v T^{1’1′}}{\sqrt{1-v^{2}}}
\end{align*}
を得る。よって\eqref{eq:symmetry-of-energy-momentum-tensor2-17}より、
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-18}
(\volume)(\Tzero, \U) \Bigr\rvert_{t’,x’} =
-(T^{0’1′} + v T^{1’1′}) \d y\wedge \d z \Bigr\rvert_{t’,x’}
\end{equation}
となった。
\eqref{eq:symmetry-of-energy-momentum-tensor2-18}の第 1 項はこれまでマル1〜マル3でも出てきたものと同類で、何を表しているのかはよくわかる。熱などの形で面マル4を通って出ていくエナジーで、 \(T^{ab}\) の \(K’\) での成分を見ることで面の運動に付随しない、「正味の」流出量が適切に計算できている。そして第 2 項こそが\eqref{eq:symmetry-of-energy-momentum-tensor2-18}の最大の注目点だ。この被積分形式は、微小時間 \(\Delta t\) をかけて微小面積 \(\Delta y \Delta z\) で積分すると、符号を除けば
\begin{equation}
\label{eq:symmetry-of-energy-momentum-tensor2-19}
T^{1’1′} v\Delta t \Delta y \Delta z
\end{equation}
となり、まさしく「壁の静止系 \(K’\) で計った、壁に垂直に働く圧力 \(T^{1’1′}\)」と「\(\Delta t\) の間に壁が動くことによる、体積の微小増加 \(v\Delta t \Delta y \Delta z\)」の積になっている。つまり確かに\eqref{eq:symmetry-of-energy-momentum-tensor2-8}の \(p \Delta V\) に相当するものが得られているわけだ。
こうして、「着目物質の、固定した慣性系での全エナジー」の時間変化について、「壁」が動く場合、熱平衡や準静過程を仮定しなくても\eqref{eq:symmetry-of-energy-momentum-tensor2-8}に相当する式が得られることがわかった。\(\delta Q\) は \(f^{0}\) による外場からのエナジー供給と、「壁」の静止系で計られる正味のエナジー流束(熱や、着目物質の輸送)の分からなり、\(p\Delta V\) は「壁」の静止系 \(K’\) で計られる、「壁」と垂直な方向の「圧力」と元の慣性系 \(K\) で計った体積の微小変化の積の、2 次元表面全体にわたる合計(積分)を表す。つまりこの表式では「\(p\)」と書いてはいてもそれはある1個の数値を表すのではなく、2 次元表面の各点ごとに「壁」の静止系で「壁」と垂直な方向に計った「圧力」を象徴的・形式的に表している。
この見方の場合、\(p\Delta V\) というのは「\(K’\) で計る値 \(p\)」と「\(K\) で計る値 \(\Delta V\)」の積になっていて、使う慣性系が揃っていないのがちょっと不自然だが、これは「この場合はそういうもの」として受け入れるしかない、という類のものなのだろう。
また、予備考察を振り返ってみると、結局全エナジー \(E\) からは、「容器」全体の並進運動からの寄与は除かれていない。実際、\(K\) での \(\U\) の成分は 3 次元領域上に渡って一様とは限らないので、「全体が静止している系」というのは自然に定義できないし、たとえ「全運動量(の空間成分)が \(0\) になる慣性系を選ぶ」ことにしても、時間経過 \(\varDelta t\) の間に(全)運動量を獲得してしまう可能性があるため、結局 \(\text{全運動量} = 0\) の条件はひとつの慣性系 \(K\) では一貫して保つことはできない(別々の時刻では、一般には異なる慣性系を要する)。したがって、これも「そういうもの」として受け入れるしかないだろう。この場合、「全体の並進運動」を与えた力による仕事は、\(\delta Q\) の中に算入されていることになる(…と思ったけど違うか?\(p\varDelta V\) の方(にも)なのか?)。
それから、\eqref{eq:symmetry-of-energy-momentum-tensor2-19}についてもう一言。これは、「力学エナジーは、行われた仕事の分だけ増加する」という極めて重要な関係が再現されたことを表している。点粒子の場合、相対論であっても運動量・(力学)エナジー・力・仕事(率)には次の関係がなりたっていた
\begin{align}
\label{eq:symmetry-of-energy-momentum-tensor2-20}
\frac{dE}{dt} &= \boldsymbol{F}\cdot \boldsymbol{v} \\
\label{eq:symmetry-of-energy-momentum-tensor2-21}
\frac{d\boldsymbol{p}}{dt} &= \boldsymbol{F}
\end{align}
が、主役が質点からエナジー運動量テンソルに移ると、その保存則\eqref{eq:symmetry-of-energy-momentum-tensor2-1}, \eqref{eq:symmetry-of-energy-momentum-tensor2-2}では実は「運動量の時間変化率 \(\boldsymbol{F}\) が、どのようにしてエナジーの時間変化率にも顔を出すのか」が直接は見えなくなっていた。そのつながりを理論上ちゃんと再現しているのが\eqref{eq:symmetry-of-energy-momentum-tensor2-19}で、ここで現れている \(T^{1’1′}\) と \(v\) の積が\eqref{eq:symmetry-of-energy-momentum-tensor2-20}の内積 \(\boldsymbol{F}\cdot \boldsymbol{v}\) に対応しているわけである(\(T^{1’1′}\) が \(\boldsymbol{F}\)、すなわち運動量の時間変化率と直接結びつくことは次節でもうちょっと詳しく見る)。
\eqref{eq:symmetry-of-energy-momentum-tensor2-20}と\eqref{eq:symmetry-of-energy-momentum-tensor2-21}は、実際には点粒子ではないある程度の大きさを持つ物体であっても高い精度でなりたっているが(物体が内部構造に乏しく、あまり変形しない硬めの物質で、自転の影響が少ない場合)、それはそういう物体が「\(T^{ab}\) の(空間的)分布が狭い範囲に集中している場合」に当たり、その結果\eqref{eq:symmetry-of-energy-momentum-tensor2-19}によって\eqref{eq:symmetry-of-energy-momentum-tensor2-20}\eqref{eq:symmetry-of-energy-momentum-tensor2-21}が再現されているからだ、と理解できる。
全運動量
ここまでの話で、\(\Tzero\) を使っていた所を \(\Ti\), \(\Tii\), \(\Tiii\) に置き換えても、形式的には類似の議論ができる。ただ、\(\Tzero\) と違って \(\Ti\), \(\Tii\), \(\Tiii\) は多くの場合は空間的ベクトルになるので、その積分曲線に沿って \(t=\text{一定}\) 超平面上の 3 次元領域を移動しても別の時刻の超平面にうまく移ってくれるとは限らず、そういった 3 次元領域での積分量を異なる時刻で比較する、という話にはうまく乗らなくなる。\(t\) ではなく \(x=\text{一定}\) 等の時間的超平面上での 3 次元領域の積分量を、異なる \(x\) 座標で比較する、等ということには自然につながりやすいが、ただそういう積分量の物理的意味が私にはよくわからないため、これと言った成果は出せていない。(何かうまい解釈が可能でしたら、教えて頂ければ幸いです)
そこで、\(\barT{i}\) については、これまでの \(\Tzero\) をそっくりそのまま置き換えることにこだわらず、物理的解釈がやりやすい形で改めて議論を作り直してみよう。以下では \(\U\) は \(U^{0}=1\) をみたす時間的ベクトルとし、3 次元領域を \(\U\) に沿って移動させて「各時刻」での 3 次元領域が定まるとしよう。
全運動量の \(x\) 成分は
\[ \int_{3} T^{10} d^{3}x \]
となるが、
\begin{align*}
T^{10} d^{3}x &= (\Ti)^{0} \d x \wedge \d y \wedge \d z \\
&= (\volume)(\Ti) \Bigr\rvert_{t} \\
\therefore \frac{d}{dt} \int_{3} T^{10} d^{3}x &= \frac{d}{dt} \int_{3}
(\volume)(\Ti) \\
&= \int_{3} \bigl\{ \Lie_{\U} (\volume)(\Ti) \bigr\}
\end{align*}
である。ここで、
\begin{align*}
\Lie_{\U} \bigl\{ (\volume)(\Ti) \bigr\} &=
\bigl\{\d ((\volume)(\Ti)) \bigr\}(\U) +
\d \bigl\{ (\volume)(\Ti, \U) \bigr\} \\
&= \div(\Ti) (\volume)(\U) + \d \bigl\{ (\volume)(\Ti, \U) \bigr\}
\end{align*}
となるから、まず自由場\eqref{eq:symmetry-of-energy-momentum-tensor2-1}の場合は \(\div(\Ti)=0\) より
\begin{align*}
\Lie_{\U} \bigl\{ (\volume)(\Ti) \bigr\} &= \d \bigl\{ (\volume)(\Ti, \U)
\bigr\} \\
\therefore \frac{d}{dt} \int_{3} T^{10} d^{3}x &=
\int_{3} \d \bigl\{ (\volume)(\Ti, \U) \bigr\} \\
&= \int_{2} (\volume)(\Ti, \U)
\end{align*}
のように、全運動量の時間微分は完全に 3 次元領域の境界の 2 次元表面上の積分のみに帰着できる。
同様にして、自由場\eqref{eq:symmetry-of-energy-momentum-tensor2-1}の場合は全運動量の(空間)成分の時間変化に対しては
\[ \frac{d}{dt} \int_{3} T^{i0} d^{3}x = \int_{2} (\volume)(\barT{i},\U) \]
が得られる。先ほどと同様に、\(x\) 軸方向の「容器」が、右端についた「ピストン」の動きで体積を変ずる場合にこの右辺を評価してみる。「ピストン」部マル4を除いた「固定壁」では
\[ (\volume)(\barT{i}, \U) \Bigr\rvert_{t} = – (\d x\wedge \d y \wedge \d z)(\barT{i}) \Bigr\rvert_{t} \]
となって、これは微小時間 \(\varDelta t\) をかければ理解しやすい「壁からの応力によって供給される力積」になる。やはり興味深いのは、「ピストン」部マル4 での状況のはずで、ふたたび \(\U\) が静止して見える慣性系 \(K’\) を取って考えると
\begin{align*}
(\volume)(\barT{i}, \U) \Bigr\rvert_{t’,x’} &=
(\d t’\wedge \d x’\wedge\d y’\wedge\d z’)(\barT{i}, \U)
\Bigr\rvert_{t’,x’} \\
&= -U^{0′}(\barT{i})^{1′} \d y’\wedge \d z’ \Bigr\rvert_{t’,x’} \\
&= -\sqrt{1-v^{2}} T^{i1′} \d y\wedge \d z \Bigr\rvert_{t,x}
\end{align*}
となる。これと
\begin{align*}
T^{11′} &= T^{\mu’1′} \frac{\partial x^{1}}{\partial x^{\mu’}} \\
&= T^{0’1′} \times \frac{v}{\sqrt{1-v^{2}}} + T^{1’1′} \times
\frac{1}{\sqrt{1-v^{2}}} \\
&= \frac{vT^{0’1′}+T^{1’1′}}{\sqrt{1-v^{2}}} \\
T^{21′} &= T^{\mu’1′} \frac{\partial x^{2}}{\partial x^{\mu’}} = T^{2’1′} \\
T^{31′} &= T^{\mu’1′} \frac{\partial x^{3}}{\partial x^{\mu’}} = T^{3’1′}
\end{align*}
から、次の結果が得られる。
\[ (\volume)(\barT{i}, \U) \Bigr\rvert_{t’,x’} =
\begin{cases}
-(vT^{0’1′}+T^{1’1′}) \d y\wedge \d z \Bigr\rvert_{t,x} & (i=1) \\
-\sqrt{1-v^{2}} T^{2’1′} \d y\wedge \d z \Bigr\rvert_{t,x} & (i=2) \\
-\sqrt{1-v^{2}} T^{3’1′} \d y\wedge \d z \Bigr\rvert_{t,x} & (i=3)
\end{cases}
\]
\(i=2,3\) の行はよくわかる。「ピストン」表面の摩擦か何かで失われる、「ピストン」表面と平行な方向の運動量を表している。\(\sqrt{1-v^{2}}\) の因子が付いているが、これは「ピストン」の静止系 \(K’\) での経過時間 \(\varDelta t’\) と元々の慣性系 \(K\) での経過時間 \(\varDelta t\) の間に \(\varDelta t’ = \sqrt{1-v^{2}}\varDelta t\) の関係があることから来る補正因子に過ぎない。一方 \(i=1\) の行はやや複雑だ。 \(T^{1’1′}\) の存在は理解できるが、\(vT^{0’1′}\) は何なのか?
これは「速度の合成」に起因する運動量の変化を補正する項なのだ。この「運動量の変化」というのは Newton 力学でも容易に理解できる話で、ある慣性系 \(K\) で \(\boldsymbol{p}=m \boldsymbol{w}\) と表される運動量を持つ質点が、別の慣性系 \(K’\) で持つ運動量 \(\boldsymbol{p}’\) は \(\boldsymbol{p}\) のままではない。\(K’\) が \(K\) に対して速度 \(\boldsymbol{v}\) を持つとすれば、\(K’\) での質点の速度は \(\boldsymbol{w}\) から \(\boldsymbol{w}’ =
\boldsymbol{w} – \boldsymbol{v}\) に変化することから、
\[ \boldsymbol{p}’ = m \boldsymbol{w}’ = m \boldsymbol{w} – m
\boldsymbol{v} = \boldsymbol{p} – m \boldsymbol{v} \]
に変化していた。したがって、\(K’\) で測定した運動量から \(K\) での運動量を逆算するには、
\[ \boldsymbol{p} = \boldsymbol{p}’ + \underbrace{m \boldsymbol{v}}_{補正} \]
という補正が必要になる。この補正に相当するのが \(vT^{0’1′}\) だ。それは次のような事情があるからだ。
\(K’\) 系で、「壁」を通して失われる正味の運動量を \(T^{1’1′}\), \(T^{2’1′}\), \(T^{3’1′}\) のみで捉えるのは適切ではない。相対論なのだから、当然エナジーと合わせて四元運動量で捉えるべきで、時間成分 \(T^{0’1′}\) も話に加わってくる。上の Newton 力学の「補正」の「質量」\(m\) に当たるものは、相対論ではこの「四元運動量の時間成分」としてのエナジーになると解釈すれば、\(i=1\) の行に現れた \(vT^{0’1′}+T^{1’1′}\) という組み合わせが自然に理解できる。\(i=2,3\) の行と違って \(\sqrt{1-v^{2}}\) の因子は消えているが、この辺りは Newton 力学と違って速度の合成則が単純な和・差にならない、といったような関係があるので、もともと完全に対応するようなものではない。「Lorentz 変換によって計算するとこうなるのだから、結果としてはこうなるものなのだ」という感じで受け入れればいい類の話だろう。
今の一連の計算は自由場\eqref{eq:symmetry-of-energy-momentum-tensor2-1}に基づくものだったが、外場があって\eqref{eq:symmetry-of-energy-momentum-tensor2-2}となる場合も同じように計算すればよい。全運動量を \(P^{1}\), \(P^{2}\), \(P^{3}\) とすれば
\begin{align*}
P^{i} &= \int_{3} T^{i0} d^{3}x \\
&= \int_{3} (\volume)(\barT{i}) \\
\frac{dP^{i}}{dt} &= \int_{3} \Lie_{\U} \bigl\{ (\volume)(\barT{i})
\bigr\} \\
&= \int_{3} \div(\barT{i}) (\volume)(\U) +
\int_{3} \d \bigl\{ (\volume)(\barT{i}, \U) \bigr\} \\
&= \int_{3} f^{i} d^{3}x + \int_{2} (\volume)(\barT{i}, \U)
\end{align*}
となり、先ほどの項に加えて、外場による運動量の供給 \(f^{i}\) の効果が入ることになる。
こんな感じで、エナジー運動量テンソルについてかなり一般的な議論を行って、重要な関係をかなり導くことができ、しかもその過程で相対論の知見を色々再確認できる、ということは、これまで私はあまり意識したことはなかった。完全流体という特殊なケースに限定する必要はないのだ。この程度なら、(微分幾何を活用している所はもうちょっと原始的な微積の話に落とし込むにしろ)相対論の教科書でも取り上げてもいい話ではないか…と思うのだが、まあ普通の教科書ではエナジー運動量テンソルにはあまり深入りしないで話を先に進める方が優先順位が高いためこんな所まで踏み込んでる余裕はなく、また紙数が増える割には具体例での計算には余り役には立たない(一般性の高さとのトレードオフ)、ということを考えると仕方ないのかもしれない。さらに、しょせん特殊相対論の範疇の話で、一般相対論になるとそのままでは使えない箇所があちこちに出てくるのでそれほど価値のある話ではないが、例によって自己満足のためにこうやって公開しておく(笑)。
摩擦のある斜めのピストン
締めくくりに、Newton 力学だと何が「正解」になるのかちょっと迷ってしまう計算を、ここまでの相対論的な枠組に従って答を出してみよう。これは、こういう話に活用できるとは調べ始めではまったく思いもしなかった話である。(あと、自分では Newton 力学の範囲内だと「正しい計算」がどちらになるのか決めかねる問題だと思っているが、もし私が見落としをしているようだったらコメント欄で教えてください)
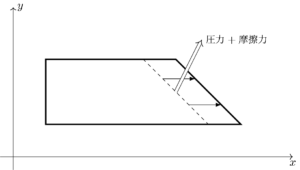
やはり、\(x\) 軸方向の容器についたピストンを考える。ただし、今度はピストンが図のような斜めの面になっているとしよう。時間経過と共に、ピストンは点線の位置から矢印のように右に進んで、実線の位置に到達する。さらに、ピストンと内部の流体の間には圧力以外に面と平行な「摩擦力」もはたらき、合力は二重矢印のように面に斜めに(非垂直に)はたらくとする。
このとき、ピストンの(3 次元)速度 \(\V{v}\) はどのように捉えるべきだろうか?素直に図の「→」の矢印だと考えると、流体がピストンに及ぼす力は、圧力だけでなく摩擦力も仕事をしていることになる。
一方、流体とピストンの接触部分のある 1 点の周辺を、微視的視点で眺めてみると、起こったことは「点線部にあった壁が実線部の位置まで後退した」ということだ。
なので、その速度は図の矢印のように、面に垂直であるという見方もできる。この場合、速度と摩擦力は垂直なので、圧力のみが仕事をしている。
この 2 通りの見方では、流体がピストンに対して行った仕事は以下の通り異なる。
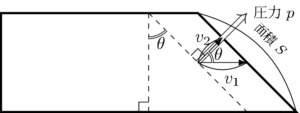
…というのは意外に感じる方も少なくないだろうから、ちょっと丁寧に計算してみる。まず、もっと普通の、圧力だけがある(すなわち摩擦力が \(0\))の場合から計算してみよう。図のように \(S\) をピストンの面積とし、角 \(\theta\) を取ってお
く。
このとき、ピストンの速度を \(v_{1}\) のように水平に取ったときに流体がピストンにした仕事は
\[ \V{F} \cdot \V{v} \varDelta t = pS \times v_{1}\cos\theta \times \varDelta t \]
で、一方、ピストンの速度を \(v_{2}\) のようにピストンと垂直に取ったときの仕事は
\[ \V{F} \cdot \V{v} \varDelta t = pS \times v_{2} \times \varDelta t \]
だから、このふたつは等しい。それはもちろん \(v_{2}= v_{1}\cos\theta\) だからであり、これによっていずれの場合も仕事が \(p\varDelta V\) といういつもの形になることもわかる。
ところが、摩擦力、すなわちピストンに平行な力の成分もあるときはそうはならない。流体がピストンに及ぼす力を、ピストンに垂直な成分と平行な成分に分けて
\[ \V{F} = \V{F}_{\perp} + \V{F}_{\parallel} \]
としたとき、圧力 \(\V{F}_{\perp}\) と \(\V{v}\) の内積は、上で計算してみた通り \(\V{v}\) が水平でも斜めでも変わらない。ところが摩擦力 \(\V{F}_{\parallel}\) と \(\V{v}\) の内積は、\(\V{v}\) を水平に取るか可動面に垂直に取るかで値が変わってしまう。 \(\V{v}\) を水平にとったときは摩擦力は仕事をし、ピストンに垂直に取った場合は仕事をしないことになってしまう。
では、実際には摩擦力は仕事をするのか、しないのか?人間が、速度の取り方を計算上変えるだけで「する仕事」という物理量が変わるなんてことがあるはずがない。熱力学第1法則(…は、狭い範囲では平衡状態どうしの間の変化のみについての法則かもしれないが、要はエナジー保存則だからそれ以外の変化に対しても拡張されなければならないはず)に照らしても、「流体が外界に行った仕事」は(慣性系が決めてあれば)一意に決まらなければならない。これが断熱過程だった場合、流体の内部エネルギーがどれだけ減るのか?は、当然ながら流体が外部に行った仕事に等しくなければいけないはずだ。
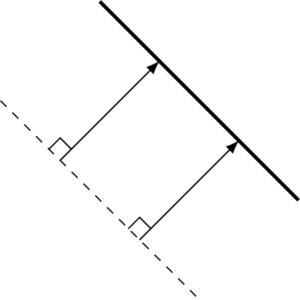
そういうわけで、何らかの方法で、「正しい」速度がどちらなのかを決めたい(あるいは、これらどちらとも違う速度が「正しい」のならそれを選び出したい)のだが、これら2通りの速度の捉え方は、「流体物質の個々の微小要素の立場」では区別できない(どちらも解釈としてありえて、一方だけを正しいと決めることができない)。「さっきまで『自分』と接していたピストン面が、\(\varDelta t\) 秒経過した今ではどこに後退しているのか」は元々決めようがないからだ。この違いは、境界面上での \(\U\) の取り方の任意性と対応している。元々、\(\U\) は 3 次元領域の 2 次元境界の軌跡に沿ったベクトルとして定められていたが、\(\U\) を定めるに当たって、図で \(\overrightarrow{\text{AB}}\) と \(\overrightarrow{\text{AC}}\) のどちらを \(\U \varDelta t\) とすべきかは任意であって決めようがない。
これは、上でも書いた通り、Newton 力学の範囲内では決めようのないことのように思える。一方、(特殊)相対論では自然な答が与えられるのだ。
先ほどの考察によると、相対論版の熱力学第1法則では、外部に行う「仕事」を決める「圧力」は、「\(t=\text{一定}\) 面を決める慣性系」と「移動する壁が静止して見える(局所)慣性系」の間の Lorentz 変換の関係から登場するものだった。この、「壁が静止する(局所)慣性系」の4元速度 \(\U\) の向きとして、\(\overrightarrow{\text{AB}}\) と \(\overrightarrow{\text{AC}}\) のどちらを選ぶべきかの指針を、自然に決めたいわけだ。この \(\U\) の向きを、時空の計量に基づいて決められれば申し分ないが、それは「直交性」に着目すれば可能だ。つまり、4 次元時空中で、着目する 2 次元境界面に、Minkowski 計量の意味で直交するベクトル \(\overrightarrow{\text{AB}}\) の方をこそ \(\U\) の向きとして採用すればいい。それが最も「自然な」決め方になる。
一見、「ピストンを構成する物質分子の速度は水平(\(x\) 軸方向)なのだから、そちらこそが『本物』の速度であって、\(\overrightarrow{\text{AC}}\) の方が正しいのではないか?」と思うかもしれない。しかし、こういう場合に考えなければならないのは、「宇宙空間中に広がった希薄なガスを囲む、仮想的な境界面」のようなものも含まれていたことを思い出そう。そういう場合、そもそも「境界面を構成する物質分子」などというものは存在しない。\(\U\) の向きを決定するのに使える材料は、\(t=\text{一定}\) を決める慣性系の他には、境界面の 4 次元時空中の軌跡(として定まる 3 次元時間的(or ヌル的)超曲面)だけしかないのだ。
また、先ほどもっと普通の、ピストンが \(x\) 軸に垂直だった場合に Lorentz 変換によって「圧力」が現れる計算を行ったが、そこでは \(\U\) がピストンに垂直だったことも思い出してほしい。あの配置では \(\U\) の最も自然で簡単な取り方が \(x\) 軸方向だったので気にも留めていなかったが、「圧力」として現れた \(T^{1’1′}\) は、エナジー運動量テンソル \(T^{ab}\) に、ふたつの 1-形式 \(\d x’\), \(\d x’\) を割り当てた値で、\(\d x’\) は明らかに「2 次元境界面の軌跡の 3 次元超曲面の外向き単位 1-形式」という意味合いを持つ。つまり、あのときの \(\U\) の取り方は、まさしくそういう慣性系 \(K’\) を特別なものとして選び出す選び方になっていたわけだ。
こういったことを考えると、四元速度 \(\U\) はやはりピストンに垂直な \(\overrightarrow{\text{AB}}\) の方をこそ選ぶべきことになる。従ってピストンの \(3\) 次元速度 \(\V{v}\) はピストンに垂直に選ぶことになり、「摩擦力は仕事をしない」のが正解、ということになる(※ ここまでの議論から明らかな通り、ここで言う「摩擦力」は、「流体とピストン(ピストン面)」の間の摩擦力のことであり、「ピストンと(ピストンが沿って動く)容器壁」の間の摩擦力のことではない)。

コメントを残す