今年は仕事の休みが取れて、MathPower を楽しんで参りました。食事などで会場を離れていたこともあったため、演目の全部は見ていなかったのですが、大変楽しかったです。加藤さんの ABC 予想の公演は非常にエキサイティングでした。観られなかった部分は、ニコニコ生放送のタイムシフトでいずれじっくり観ようと思っています。
演目のひとつ「数学の決闘」の予選問題に、この blog で以前触れた問題を採用していただいたのですが、解答の公開が滞っているようなので、こちらで公開しようかと思います。
また、決勝の問題1は(私にとっては)大変手強い問題で、解くのに 1 週間以上もかかってしまいました。模範解答はどんな風なのか割と楽しみにしているのですが、中々公開されないので、参考までに私の解答も掲出しておきます。
数学の決闘・予選第3セット 第2問解答
循環節の長さを \(6l\) とおく。\(1 \div p\) の筆算の割り算が次のようだったとする。
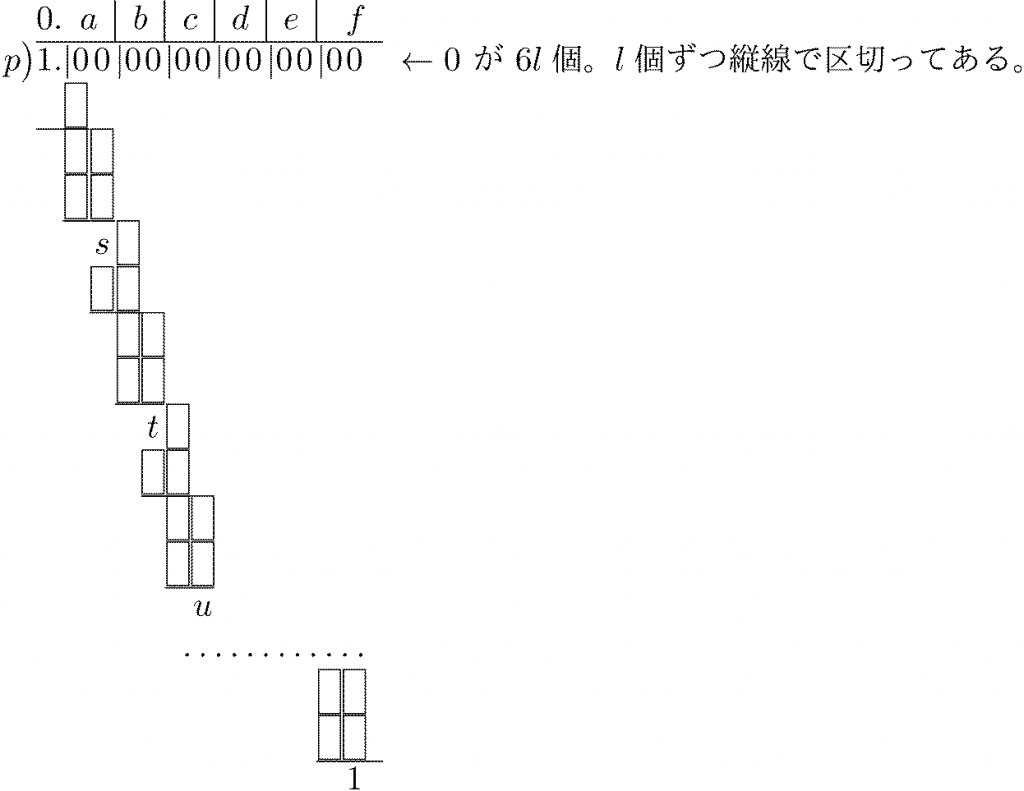
最後、\(6l\) 桁目で右下の余りに \(1\) が初めて現れ、ここから計算が始めに戻って循環する。また、余りに \(1\) が現れるより前に商で一足先に循環が起きることはない(余り \(r\) から商が循環したとすると、\(1 \div p\) と \(r \div p\) が同じ値(無限小数)になることになるので \(1=r\) になるしかない)。
この筆算の図を整数の割り算と読み替えると、\(10^{6l}\) を \(p\) で割った余りが \(1\) ということだから
\begin{align*}
10^{6l} &\equiv 1 \pmod{p} \\
\therefore (10^{3l}-1)(10^{3l}+1) &\equiv 0 \pmod{p} \\
\therefore 10^{3l}-1 &\equiv 0 \pmod{p} \text{ or } 10^{3l}+1 \equiv 0 \pmod{p} \quad (\because \text{$p$ は素数}) \\
\therefore 10^{3l} &\equiv \pm 1 \pmod{p}
\end{align*}
だが、もし \(10^{3l} \equiv 1 \pmod{p}\) だったら \(1 \div p\) は \(3l\) 桁で循環してしまうので \(10^{3l} \equiv -1 \pmod{p}\) である。これは、図で余り \(u\) が出てくる所までを \(10^{3l}\) の割り算と読み替えると、\(u=p-1\) であることを意味する。
図のように余り \(s\), \(t\) を定めると \(10^{l}\) を \(p\) で割った商が \(a\) で余りが \(s\) 、\(s\cdot 10^{l}\) を \(p\) で割った商が \(b\) で余りが \(t\)、等であるから
\begin{align}
10^{l} &= pa + s\label{223941_15Sep17} \\
s \cdot 10^{l} &= pb + t\label{223948_15Sep17} \\
t \cdot 10^{l} &= pc + p-1 \quad (\because u=p-1)\label{223955_15Sep17}
\end{align}
である。\(\eqref{223941_15Sep17} – \eqref{223948_15Sep17} + \eqref{223955_15Sep17}\) を作ると
\begin{align}
(1-s+t)10^{l} &= p(a-b+c) + s-t+p-1 \notag\\
\therefore (1-s+t)(10^{l}+1) &= p(a-b+c+1)\label{224927_15Sep17}
\end{align}
だから、\((1-s+t)(10^{l}+1)\) が素数 \(p\) で割り切れる。よって
\[ 1-s+t \equiv 0 \pmod{p} \text{ or } 10^{l} \equiv -1 \pmod{p} \]
だが、もし \(10^{l} \equiv -1 \pmod{p}\) だと \(10^{2l} \equiv 1 \pmod{p}\) で \(1 \div p\) が \(2l\) 桁で循環してしまうので \(1-s+t \equiv 0 \pmod{p}\) でなければならない。すなわち \(t-s+1\) は \(p\) の倍数である。
ここで、\(s\), \(t\) はいずれも「\(p\) で割った余り」なので \(p-1\) 以下で、また \(0\) ではない(\(1 \div p\) が無限小数になったので、途中で割り切れることはない)から、
\begin{align*}
-(p-2) &\leqq t-s \leqq p-2 \notag\\
\therefore -p+3 &\leqq t-s+1 \leqq p-1
\end{align*}
すなわち \(-p < t-s+1 < p\) だが、この範囲にある \(p\) の倍数は \(0\) しかないので \(t-s+1=0\) である。
これを\eqref{224927_15Sep17}に代入すれば
\begin{align*}
p(a-b+c+1) &= 0 \\
\therefore a-b+c &= -1
\end{align*}
である。\(\square\)
なお、以前の記事で書いた通り、循環節の長さが \(2\) や \(3\) の倍数であるとき、\(2\) 等分・\(3\) 等分したそれぞれを足すとどちらも \(9\) が並ぶ数になりますが、その結果を使って示すこともできます。
数学の決闘・決勝第1問解答
\(f(x) = 0*x\) とおくと、与えられた条件から次の式がなりたつ。
\begin{align}
f(f(x)) &= f(x)\label{161821_17Oct17} \\
f(x) * y &= x * f(y) = f(x) * f(y)\label{155505_17Oct17} \\
x * y &= x + f(y-x)\label{231746_17Oct17} \\
f(-x) &= f(x) – x\label{155313_17Oct17}
\end{align}
特に\eqref{155505_17Oct17}で \(x’=f(x)\) とおくと
\begin{equation}
x’ * y = x’ * f(y)\label{231557_17Oct17}
\end{equation}
が得られ、これは次のことを意味する。「\(x’\) が \(f\) の値域の数なら、任意の \(y\) に対し\eqref{231557_17Oct17}がなりたつ」
\(f(1)=A\) とおく。\eqref{155313_17Oct17}によって \(f(-1)=A-1\) である。
自然数 \(n\) に対し \(f(n)=nA\) であることを示すことを当面の目標とする。まず、\(0\) 以上の整数 \(n\) に対し次のことを示す。
\begin{equation}
f(nA+1) = (n+1)A\label{155216_17Oct17}
\end{equation}
[証明]
- \eqref{155216_17Oct17}は \(n=0\) のときは成立している。
- \(n\) が自然数で\eqref{155216_17Oct17}が \(n-1\) に対してなりたつとしよう。すると \(nA\) が \(f\) の値域に入るので、\eqref{231557_17Oct17}を \(x’=nA\), \(y=-1\) に対して使って
\begin{align*}
nA * (-1) &= nA * (A-1) \\
-1 + f(nA+1) &= A-1 + f((n-1)A+1) \quad (\because \eqref{231746_17Oct17}) \\
&= A-1 + nA \\
\therefore f(nA+1) &= (n+1)A
\end{align*}
によって\eqref{155216_17Oct17}は \(n\) に対しても成立している。
以上で\eqref{155216_17Oct17}は \(n \geqq 0\) に対し示された。
するとさらに、自然数 \(m\), \(n\) に対し次のことがなりたつ。
\begin{equation}
f\bigl( (n-m)A + m \bigr) = nA\label{161705_17Oct17}
\end{equation}
[証明]
- \eqref{161705_17Oct17}は \(m=1\) のとき成立している。
- \(m\) が自然数で\eqref{161705_17Oct17}が \(m\) に対し成立しているとしよう。\(A-1=f(-1)\) が \(f\) の値域に入るので、\eqref{231557_17Oct17}を \(x’=A-1\), \(y=(n-m)A+m\) に対して使うと、
\begin{align*}
(A-1) * \bigl( (n-m)A+m \bigr) &= (A-1) * nA \\
A-1 + f\bigl( (n-m-1)A + m+1 \bigr) &= A-1 + nA \quad (\because \eqref{231746_17Oct17}) \\
\therefore f\bigl( (n-m-1)A +m+1 \bigr) &= nA
\end{align*}
なので\eqref{161705_17Oct17}は \(m+1\) に対しても成立している。
以上で\eqref{161705_17Oct17}は任意の自然数 \(m\), \(n\) に対し示された。
\eqref{161705_17Oct17}で \(m=n\) とすることにより、任意の自然数 \(n\) に対し
\begin{equation}
f(n) = nA\label{173004_17Oct17}
\end{equation}
も示された。したがって、もし \(A>0\) であるなら \(f(A)=A^{2}\) だが、一方\eqref{161821_17Oct17}より \(f(A)=f(f(1)) = f(1)=A\) でもあるから、\(A^{2}=A\) である。よって \(A>0\) の場合は \(A=1\) しかありえない。
また、\(A<0\) の場合は\eqref{155313_17Oct17}で \(x=A\) とおくことにより \(f(-A) = f(A)-A = 0\) だが、一方\eqref{173004_17Oct17}で \(n=-A\) とおくと \(f(-A) = -A^{2}\) でもあるので、\(-A^{2}=0\) となって \(A<0\) に反する。
よって、\(A=0, 1\) のどちらかしかありえない。
- \(A=1\) のとき
\eqref{173004_17Oct17}から任意の自然数 \(n\) に対し \(f(n)=n\) で、これと\eqref{155313_17Oct17}より \(f(-n) = f(n)- n=0\) である。すなわち
\[ f(x) =
\begin{cases}
x & (x \geqq 0) \\
0 & (x < 0)
\end{cases}
\]
である。すると、\(a \leqq b\) に対し
\[ a * b = a + f(b-a) = a+b-a = b \]
となるので、\(a * b = \max\{a, b\}\) である。 - \(A=0\) のとき
\eqref{173004_17Oct17}から任意の自然数 \(n\) に対し\(f(n)=0\) で、これと\eqref{155313_17Oct17}より \(f(-n)=-n\) である。すなわち
\[ f(x) =
\begin{cases}
0 & (x \geqq 0) \\
x & (x < 0)
\end{cases}
\]
である。すると、\(a \leqq b\) に対し
\[ a * b = a + f(b-a) = a+0 = a \]
となるので、\(a * b = \min\{a, b\}\) である。
以上から、二項演算 \(*\) は max, min のいずれかしかありえない。逆に、max, min のとき与えられた条件をすべてみたす。
よって答は max および min である。\(\square\)
数学的帰納法を 2 回使うのがいかにも冗長で、1 回にまとめられるんじゃないかと思っているんですが、うまい手が思いつかなかったのでこのような不格好な形のまま晒すこととします。
コメントを残す