先日、http://tsujimotter.hatenablog.com/entry/2014/04/08/213019 にて次のような面白い話を見かけて「へえ」と感心した。
\(\dfrac{1}{7}=0.142857142857\dots\) のように、\(\dfrac{1}{\text{素数}}\) が無限小数になるとき、その循環節 \(142857\) の桁数が偶数ならば、半分ずつに分けて足し合わせると
\[ 142+857 = 999 \]
のように \(9\) が並ぶ。
リンク先の記事によると Midy の定理というようだ。
さらにその1つ前のエントリ http://tsujimotter.hatenablog.com/entry/2014/04/08/212954 も読んでみたところ、そこでは Fermat の小定理から
\(\dfrac{1}{p}\) は \(p-1\) 桁で循環する(\(p\) は \(2\) でも \(5\) でもない素数)……… ☆
ということを証明している。これについては、私は http://math.artet.net/?eid=148142 での \(p=7\) の場合を例にとった話の方がずっとあっさりしていて好みだ。割り算の筆算の様子を具体的に図示することによって、何がどうなっているかのメカニズムが一目で把握できるところがいい(リンク先の話は、実際には Fermat の小定理「からの帰結」として説明しているわけではなくて、Fermat の小定理「に馴染むための試みのひとつ」として挙がっているのだが、Fermat の小定理を既知とする立場からは図式一つで☆の明快な説明となっている)。
で、ちょっと自分でも考察を進めてみると、Midy の定理の方も、割り算の筆算を軸にすると、最初の記事の証明よりもあっさり示せることに気づいた。「これくらいのことはどうせ気づいている人がたくさんいるだろう…」と思って Midy の定理を web で検索してみると、意外や意外、どうも私のような示し方をしている人は見当たらない。いや、別に網羅的に調べたわけではなく単に検索結果上位の方をある程度当たってみただけだが、日本語でも英語でも、似たり寄ったりのやや回りくどい(私の主観)示し方になっているものばかりだった(もっとも、割り算の筆算の様子を (La)TeX で書くのは面倒だしスペースも食うので、筆算の割り算を通じた形で理解している人でも「内容的にはそれと同等な数式の集まり」のぎこちない見かけで敢えて書いているだけ、ということはあってもおかしくない)。
それで、職場の、この手の話に詳しい人に聞いてみた所、彼はさすがにこれが「わかっていればすごくあっさり明快に説明できる話」だということを知っていた(電車の中の立ち話だったので、私の理解が完全に彼と同じ形かどうかまでは不明だが、あの話しぶりからするとおそらく大差はないだろう)。
というわけで、やはり知っている人にとっては当然の話で新味はないだろうが、web 上で公開するのは意味はありそうなので、Midy の定理の(自分にとっては)すっきりした証明を紹介しようと思う。上で紹介した http://math.artet.net/?eid=148142 の内容(及び合同式の基本)は既知とする。
ここでは、以下のものを「Midy の定理」と呼んでおく(オリジナルはちょっと違った形で述べられているらしいがちゃんと調べていない。乞御容赦)。
\(p\) を \(2\), \(5\) 以外の素数とするとき、\(\dfrac{1}{p}\) を無限小数に表したときの循環節の桁数が偶数なら、それを \(2\) 分割して足し合わせると \(9\) が並ぶ数になる。
やはり、\(p=7\) の場合を例にとって説明する。\(\dfrac{1}{p}\) を無限小数に表したときの循環節は \(142857\) であり、\(1 \div p\) を筆算で計算した様子を次のように書いておく。計算の詳細は実は必要ないので、箱で隠しておく。

この割り算の図式を整数の割り算と読み替えると、循環節の前半 \(a=142\) は\(1000 = 10^{3}\) を \(7\) で割ったときの商であり、そのときの余りは★だから、
\[ 10^{3} = 7a + \text{★} \]
と書ける。実は、★は実際に計算することなく出せる。
まず、\(10^{6} \equiv 1 \pmod{7}\) だったが、これより \(10^{3} \equiv \pm 1 \pmod{7}\) である(\(\because 7\) は素数)。もし \(10^{3} \equiv 1 \pmod{7}\) だったら \(\dfrac{1}{7}\) は \(3\) 桁で循環してしまうので \(10^{3} \equiv -1 \pmod{7}\) でなければならない。よって★は \(p-1 = 6\) である。つまり次の等式が成り立つ。
\begin{equation}
\label{eq:40-1}
10^{3} = 7a + 6
\end{equation}
次に、★から後の割り算の進行を整数の割り算と読み替えると、これは結局 \(\text{★}000 = 6 \times 10^{3}\) を \(7\) で割る計算と同じであり、その商が循環節の後半 \(b=857\) で余りが \(1\) になっているということがわかる。よって
\begin{equation}
\label{eq:40-2}
6\cdot 10^{3} = 7b + 1
\end{equation}
である。
\eqref{eq:40-1}, \eqref{eq:40-2}を辺々足すと
\begin{align*}
7 \cdot 10^{3} &= 7(a+b) + 7 \\
\therefore 10^{3} &= a+b + 1
\end{align*}
で、これより \(a+b=10^{3}-1\) となって \(9\) が並ぶことがわかる。\(\square\)
以上の流れならば、特に大小評価などするまでもなく、\(a+b\) の値がダイレクトに出てくる。
なお、職場で初等整数論講義(高木貞治)を眺めると、この性質はやはり筆算の割り算を図示した上で、以下のようにサラッと説明されていた(Midy の定理という名前こそ出ていなかったが)。“…ここでは \(e=6\) だから、\(10^{3} \equiv -1 \pmod{7}\) 故に上記の割り算で第三段の剰余が \(6 \equiv -1 \pmod{7}\) である。\(1/7\) と \(6/7\) の和が \(1\) であるから上記のような現象が生ずる。”\eqref{eq:40-1}, \eqref{eq:40-2}のように整数の割り算に帰着せず、無限小数のまま示せる、というわけで、さすがに私など足下にも及ばない切れ味の鋭さだ。なおこの説明は細部をやや省略気味で、なぜそれで説明になっているのか多少の考察が必要だが、それをわざわざ説明してしまうのは野暮なので、「なぜだろう?」と思う方は是非自分で考えてみていただきたい。
(ちなみに、冒頭の話で触れた blog では、☆の証明は初等整数論講義を参考にした、となっているが、それならば Midy の定理の証明もやはり初等整数論講義に倣えば簡明に済んだのではないか。なお、上のようにサラッと示せていることから、☆が割り算の筆算で明快に説明できることも高木貞治は当然知っていたのだろう。その上で、☆の証明では敢えてやや回りくどい道筋を採ったものと思われる)
【 2015, 10/24 追記 】
補足: \(1 \div p\) を筆算で計算したとき、\(p-1\) 桁で循環するときの余りというのは、Fermat の小定理によって \(1\) になっていた。同様に、計算の過程で余りに \(1\) が出現したらそこで必ず循環する、と言えるわけだが、これ自身はその逆の「循環が始まる直前に現れる余りは \(1\) である」ことを直接保証するわけではない。Fermat の小定理も「\(p-1\) 桁目では」余りが必ず \(1\) である、ということを保証するだけであり、実際の循環節が \(p-1\) より短いときにそこの余りが \(1\) になるかどうかはまた別の話になる。
通常、そのことは http://tsujimotter.hatenablog.com/entry/2014/04/08/213019
で行われているような「\(10^{e}\) 倍して元の数を引く」という式変形を通じて示されるが、ここではせっかくなのであくまで筆算の割り算の図式に基づいても説明できることを示しておく。
\(1 \div p\) を筆算で計算しているとき、循環が始まる直前に現れる余りを \(r\) とすると、そこから先の計算の進行は \(r \div p\) の計算と一致するわけだが、その時の商が \(1 \div p\) と同じ循環無限小数になるわけだから、\(\frac{r}{p} = \frac{1}{p}\) ということになる。よって \(r=1\) でなければならない。このことによって、上の議論で筆算の一番右下に現れる余りが \(1\) であることが保証される。この説明は、上で触れた「この手の話に詳しい人」のお陰である。彼に感謝を捧げる。
さらに、Midy の定理を「\(2\) 等分」から「\(3\) 等分」に拡張した以下の性質(Ginsberg の定理というらしい)も、やはり筆算の割り算を使って見通しよく示せる。
\(p\) を素数とする。\(\dfrac{1}{p}\) が無限小数になり、その循環節の桁数が \(3\) の倍数になるとき、循環節を \(3\) 等分して足し合わせると \(9\) が並ぶ数になる。
やはり \(p=7\) の場合を例に取ると、\(\dfrac{1}{7}\) の循環節 \(142857\)(\(6\) 桁)を \(3\) 等分すると \(14\), \(28\), \(57\) になり、これらを足し合わせると
\[ 14 + 28 + 57 = 99 \]
となって確かに \(9\) が並んでいる。この性質を一般の素数に適用できる形で証明しよう。
やはり \(1 \div 7\) の筆算の様子を書いておく。
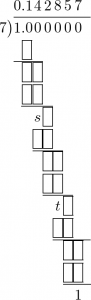
循環節を \(3\) 等分したそれぞれを \(a=14\), \(b=28\), \(c=57\) としておこう。\(s\) は \(10^{2}\) を \(7\) で割った余りでその商が \(a\) だから
\[ 10^{2} = 7a + s \]
である。同様に、
\begin{align*}
s \cdot 10^{2} &= 7b + t \\
t \cdot 10^{2} &= 7c + 1
\end{align*}
がなりたつから、辺々足すと
\begin{align}
(1+s+t)10^{2} &= 7(a+b+c) + (s+t+1) \notag\\
\label{eq:40-3}
\therefore (1+s+t)(10^{2}-1) &= 7(a+b+c)
\end{align}
よって \((1+s+t)(10^{2}-1) \equiv 0 \pmod{7}\)。ここで、\(10^{2}-1 \not\equiv 0 \pmod{7}\)(なぜならば、もし \(\equiv 0\) ならば \(\dfrac{1}{7}\) は\(2\) 桁で循環してしまうから)だから、結局 \(1+s+t \equiv 0 \pmod{7}\) (\(\because p=7\) は素数)。
一方 \(s\), \(t\) は \(p\) で割った余りなので共に \(p-1\) 以下だから
\[ 1+s+t \leqq 1 + (p-1) + (p-1) = 2p-1 < 2p \]
したがって \(1+s+t\) は \(p=7\) の正の倍数で \(2p\) 未満なので \(p=7\) に等しい。よって\eqref{eq:40-3}より
\begin{align*}
7(10^{2}-1) &= 7(a+b+c) \\
\therefore 10^{2}-1 &= a+b+c
\end{align*}
で、\(a+b+c\) は \(9\) が並ぶ数。\(\square\)
この議論では \(s\), \(t\) の具体的な値を必要としていない。同様に議論すれば、上の Midy の定理の証明でも、実は★を \(p-1\) と具体化せずに証明することは可能(その場合は、\(a+b = 10^{3}-1\) を導く過程で類似の大小評価が挟まる)。
なお、\(3\) 分割をさらに \(4\) 分割、\(5\) 分割…に拡張した場合(Lewittes の定理というらしい)は、分割後の和が \(99\dots 9\)「の倍数」になる所までしか言えず、ぴったり \(99\dots9\) になるとは言えない(上の議論の「\(2p\) 未満」に当たる所の上限が大きくなってしまうため)。実際反例もあり、\(p=101\) のとき
\[ \dfrac{1}{101} = 0.00990099\dots \]
で循環節は \(0099\) の \(4\) 桁だが、\(4\) 分割して足すと \(0+0+9+9=18\) で \(9\)「の倍数」にしかならない。
この拡張版の証明は、\(2m\) 分割の場合は \(2\) 分割の場合の結果から直ちに \(99\dots9\) の \(m\) 倍になると言えるわけだが、奇数の場合でも上の議論をちょっと手直しするだけで可能で、\eqref{eq:40-3}に当たる式から「\(p(a+b+\dots)\) が \(10^{l}-1\) の倍数」とわかるので、これと \(10^{l}-1 \not\equiv 0 \pmod{p}\) および \(p\) が素数であることによって「\(a+b+\dots\) が \(10^{l}-1\) の倍数」と言える。
コメントを残す