\(\newcommand{\V}[1]{\boldsymbol{#1}}\)
押した棒を離すパラドックス
だいぶ以前だが、相対性理論について面白いパラドックスを見かけたことがある。
極端大仏率Returns!“相対性理論はやはり間違っていた!”
これは非常に面白かった。「静止系では棒の加速はないはずなのに、運動系では加速が生じるはず。そして『加速のあるなしは慣性系の取り方によらない』のでこれは矛盾している」あるいは、「静止系では棒の速度は \(0\) のまま変わらないので、運動系でも速度は一定で変わらない。ということは運動量の変化もないはず。ところが運動系では \(0\) でない正味の力積を受け取っているので、前後での全運動量は変化しなければならない。これは矛盾している」というのは確かにパラドキシカルで、最初にこれを読んだ時にはかなり混乱して、なかなか解決に至らなかった。
同じ方による解決編
極端大仏率Returns!“「相対性理論はやはり間違っていた!」はやはり間違っていた!”
は、メイン部分はなぜその話がこの問題の解決になっているのか私にはよくわからなかったが、補足として書かれていた
運動量が変化してもなぜ速度は一定なのかというのは説明が必要かもしれない。これは相対論では速度の変化だけでなく、質量(=エネルギー)の変化も運動量を変えるということを考えれば理解できる。つまり、棒は S’ で一定の速度で動いているのだが、質量の変化分だけ運動量が変わるのである
という説明は明快で、これで上述の2点のうち後者の理由はよく理解できた。
以下、前者のパラドックスはどうすれば解決するのか、自分なりの説明を書いてみようと思う。また、後者についてももう少し掘り下げてみる。
元記事にならって、棒が静止している始めの慣性系を \(S\)、棒が動いて見える慣性系を \(S’\) としよう。運動の向きが明記されていないようだが、あいまいさがないよう、ここでは \(S’\) から見て棒は右側に向かって動いているとする。さらに、棒を押さえている人は \(S\) 系、\(S’\) 系の観測者と同じ向きを向いていて(向かい合ってはいない)、棒の右側を押さえているのが右手、左側を押さえているのが左手だとする(大方のコメントもこれらを前提として書かれているように思える)。
すると、\(S’\) から見て先に棒から離れるのは左側を押していた左手である。左手が離れても、\(S’\) では右手が離れるまで多少の時間があり、その間右手は棒の速度と反対向きに力を加え続けている、というのがこのパラドックスの根源になっている(元記事では“棒は右向きに押されて加速されるはずである”と書かれているが、おそらくこれはちょっとした思い違い・書き間違いの類で、実際には棒は「右手から左向きに押されて減速される」はず)。これを解決するために、\(S’\) で左手が離れてから右手が離れるまでの間、どういうことが起こっているのかをもっと詳しく分析してみよう。考えやすくするため、ビデオをスロー再生している感覚で、すべてのものごとがうんとゆっくり進行している…というイメージを持って頂くとよいだろう。
まず、左手が離れたとき、その情報は棒全体に瞬時には伝わらない。それまで棒の内部は一定の圧力で釣り合っていたわけだが、左手が離れたことにより圧力は急激に減少する。その減少は棒の中を「徐々に」伝わっていき、それには(\(0\) でない)有限の時間を必要とする。つまり、左手が離れた直後のしばらくの間に起きることは、次のようになっている。
右端の状態: それまでと何も変わらない。つまり棒の内部からの圧力と右手から押される力が釣り合っていて、棒の右端(の面上の分子たち)はそれまでと変わらない速度での等速直線運動を続ける。
左端の状態: 棒の内部からの圧力はまだ残っているが、左手から押される力がなくなったので、棒の左端(の面上の分子たち)は左向きの正味の力を受け、加速度を持つ(進行方向逆向きの加速度なので、減速することになる)。
つまり、やはり \(S’\) での加速度運動は起きるのだ。だがそれは「棒全体が」加速(減速)されるのではなく、最初は左端だけが加速(減速)を受ける、という形で始まる。
圧力の減少が棒の中を右向きに伝わっていくにつれ、棒の中で加速度を持つ部分も広がっていく。棒は基本的には弾性体と思ってよいはずだから、ちょっとの間左向きに加速されていた左端も、しばらく経つとバネが縮むのと同様な反動で右向きに引き戻される力を受け、右向きの加速度を得るだろう。この繰り返しで、棒の左端は単振動的なブルブルとした振動を起こす。これは左端以外の場所でも同様で、左端とはタイミング(位相)はずれるが振動が起きる。これは要するに棒(の左端に近い部分)が弾性体として振動するということで、この振動が弾性波として棒を伝わっていく、というのが起きる現象である。
というわけで、「加速度があるのかないのか」と言ったら「ある」というのが答だ。ただそれは「棒全体が一体となって加速度運動をする」のではなく、「力の加わり方に変化が起きた所からスタートして徐々に加速度を持つ部分が広がっていく」という形であって、棒全体としては「加速度を持つ部分と持たない部分が混在する、加速度を持つ部分も、その加速度の向きや大きさは場所ごとにバラバラ」という状態になる。
そして、同じことが \(S\) から見た場合にも言えることがわかるだろう。始めに述べた通り「物体が加速度を持つかどうか」は慣性系の取り方によらない概念なので、\(S\) から見ても「手を離した直後から、棒の端点が加速度運動を始める」ことは変わらない。つまりもともとのパラドックスの源だった「\(S\) から見ると棒の加速度はない」という言明が、こういった細部を見ない雑な表現だったのだ。実際に起きることは「棒の中には、加速度を持つ部分もあれば持たない部分もある」ということで、「棒の端点から加速度運動が始まり、加速度を持つ部分が端からだんだん広がっていく。弾性波が端から内部へ伝わっていく」ということが \(S\) でも \(S’\) でも同様に起きるのである(だから相対論では完全剛体というのは存在できない。どれほど頑丈な物体であっても、(\(0\) でない)有限の大きさを持つものならば、手で押さえれば(ちょっとは)歪み、手を離すと(ちょっとは)加速度運動を起こす、ということは避けられないことになる)。
\(S\) で見ると、右手も左手と同時に棒から離れるので、棒の右端でも左端とまったく同様なことが起こり、加速度運動が始まって弾性波が端から内側に向かって(つまり右から左に向かって)伝わっていく。このことが \(S’\) で見るとどうなっているかを続いて考えてみよう。
\(S’\) で棒から右手が離れるのは、左端で発生した弾性波が右端に到達するよりも前だ。なぜなら、棒からそれぞれの手が離れる事象(時空点)は Minkowki 幾何の意味で空間的に隔たっており、「弾性波の伝搬」という因果律に沿った(光速より遅い)現象で結ばれることはないからだ。棒の内部構造・弾性波の伝搬の仕方の詳細によらず、必ず右手の離脱が先行して起こり、その結果棒の右端でも弾性波が発生し左に向かって伝搬し始める(この時点で、棒の右端も加速度運動を始めることになる)。
こうやって右端から発生した弾性波は左端から来た弾性波といずれぶつかることになる。元々棒が左右対称だった場合は、棒のちょうど中点で弾性波はぶつかる。これは、次のように考えればわかる。まず、\(S\) では対称性によってちょうど中点でぶつかることは明らか。そういう「空間的な隔たりのない \(1\) 点で、ある時刻に起きた現象」は時空内の \(1\) つの時空点で表される事象(event)だから、「その事象が棒の中点で起きたかどうか」は慣性系の取り方によらず決まる。
したがって、\(S’\) 系では、左端で発生した弾性波が棒の中点に伝わるより前に右手が棒から離れ、そこで発生した弾性波が左に伝わっていって、\(2\) つの弾性波がちょうど棒の中点で出会う、というのが(元々棒が左右対称だった場合に)起きる現象である。
こういったわけで、元々の「棒は加速度運動をするのか、しないのか?」という問いは、そもそも問いの立て方が適切ではない。この問いは「棒全体が一体となって動く」という暗黙のうちの思い込みを前提とした問いであり、その前提が崩れてしまったからにはもはや考慮すべき意味を失ってしまうからだ。
そろそろ「スロー再生」は打ち切ろう。簡単のため、以降棒が左右対称だった場合のみを考える。この時、\(S\) で見ると手を離したあとの棒は伸び縮みを繰り返すが、対称性によってタイミングが左右で完全に同期しており、棒の中心はずっと静止したままだ。内部で散逸があれば段々振動は小さくなり、やがて止まるだろうし、そうでなければ振動はいつまでも続くことになる。これを \(S’\) で見れば、先に左手が離れて左端から振動が始まり、後から右手も離れて右端からも振動が始まる。しばらくすると棒全体のほとんどの場所が振動しているようになり、そのタイミングは左右で同期しているわけではないが、棒の中点だけは手を離す前からずっと一貫して同じ速度での等速直線運動を保ち続ける、ということになる。つまり、棒の中点だけ見れば、手を離す前も後も、どちらの慣性系でもまったく加速度を持っておらず、やはり矛盾はない。
続いて、力積と運動量の関係の考察に移ろう。簡単のため、棒の内部では散逸があり、手を離した後の振動はやがて収まるとする。\(S’\) 系では、両手ともまだ棒を押さえていた時期と、両手とも離れた後の時期では棒に与える合力は \(0\) なので、それらの時期中に棒に与えられる正味の力積はいずれも \(0\) である。よって「左手が離れる前の棒の全運動量」は一定で、「右手が離れた後の全運動量」も一定である。問題は、左手が離れてから右手が離れるまでの間で、この間は右手のみが力を与えているので、棒には左向きの正味の力積が与えられている。したがって、「左手が離れるより前の棒の全運動量」よりも「右手が離れた後の全運動量」の方が減っていないといけない(右向きを正として)。一方、中点の速度が \(S’\) でも一定であることから、振動が収まった後の棒全体の速度は、手を離す以前の速度と同じ、ということになる。すると \(S’\) では速度が変わらないのに運動量が変わっており、これは質点だったら矛盾になる。
が、棒の場合は上で引用した通り「棒の質量」は「棒のエネルギー」であって、それは変化し得るので、矛盾を回避することができる。速度が変わらないのに運動量が減ったということは、質量(エネルギー)は減少したということになる。なぜ減少したのかを探るために、\(4\) 元運動量を \(S\) で見たらどうなるかを調べてみる。今、運動量を
\[ \V{P} = \frac{M \V{v}}{\sqrt{1-v^{2}}} \]
と表せば(\(c=1\) の単位系を使った)、質量は \(M\) であり、さらにそれは \(4\) 元運動量 \(P^{\mu}\) のノルムと
\[ -P^{\mu}P_{\mu} = (P^{0})^{2}- \V{P}^{2} = M^{2} \]
という関係にある(添字の上げ下げと Einstein の総和記法については標準的な記法に従う。ここでは計量の符号は \(-+++\) 型とする)。この左辺 \(-P^{\mu}P_{\mu}\) は慣性系の取り方によらないので、\(S\) で計算しても同じ値 \(M^{2}\) になる。\(S\) では棒はずっと静止しているため \(\V{P}=\V{0}\) であり、よって \(S\) での \(4\) 元運動量は
\[ (P^{0}, \V{P}) = (M, \V{0}) \]
というベクトルなわけだ。この \(M\) の値が \(S’\) では手を離した後に減っているので、\(S\) でもエネルギー \(P^{0}=M\) の値が、手を離した後には減っていることになる。
何で減るのか?\(S\) では左右同時にパッと手を離すのだから、棒のエネルギーは一定のはずだ。するとこれはまた新たなパラドックスになるのか?
そうではない。\(S\) 系で棒のエネルギーが減少する余地はちゃんとある。唯一の機会は「手を離すときに棒が僅かに膨張するが、その時棒が手に対して仕事をする(※ 注)」ということだ。これ以外にエネルギーが減少する余地はない(棒が電荷を帯びていて電磁場に浸されている…とかなら別だが、手との力学的相互作用しかないとすればこれだけのはず)。
と、いうことはだ。
この問題で、棒から手を離すとき、完全に「一瞬で」パッと離す、ということは決してできない、ということだ。なぜなら \(M\) の減少は避けられないのだから。どんなに急いで離しても、棒の表面が手を追っかけて膨張してくる速度を上回って手が棒から仕事を受けないように手を動かすことは不可能で、棒は必ず手に対して仕事をする、ということになる。これは相対論から課される制約だ。先ほど、相対論では棒が完全剛体になることはありえない、という話が出たが、それだけでなく、(一見すると問題なさそうな)「手を離すとき棒との接触が完全になくなるまでの時間はいくらでも小さくすることができるから、『離す際に棒が手にする仕事』はいくらでも小さくでき、理論上は \(0\) に理想化してよい」という想定も正しくない、ということになる。このことは不合理にも思えるが、恐らく「棒を押さえていた手もまた完全剛体たりえないので、押さえていた力をいくら急激に減少させても、手の弾性があるため棒から仕事を受けることを完全にはなくせない」ということがそういう制約になって現れているのだろう。
※ 棒のエネルギーの増減に関わるのは、正しくは「棒が手(外力)によって『される』仕事」であって、「棒が手に『する』仕事」の方ではない。今の場合は「される仕事」と「する仕事」は符号が違うだけで同じ大きさを持つので、両者を厳密に区別しないラフな言い方を採るが、場合によってはそういうシンプルな関係は崩れることがあるので注意(分子運動的な微視的な相互作用を粗視化して、「摩擦」等の形で現象論的に扱う場合にそういうことが起こりうる)。ここで「棒が(手に)する仕事」と言ってる部分は、実際にはすべて「棒が手(の及ぼす力)によってされる負の仕事」である。
この「相対論では、棒が手に対して仕事ができないくらい素早く手を離すことは不可能」ということは、時間反転したプロセスを考えるとよりはっきりするだろう。今の話とは逆に、自由状態で静止していた棒を、ある時刻で左右から同時に手で押さえたとすると、どんなに「素早く」力を加えたとしても、ほんの僅かは縮んで、棒は手に仕事をされる。したがって棒の持つエネルギーの上昇は避けられない。この過程を、やはりビデオを再生している感覚で、今度は逆回しで見れば、最初手で棒を押さえていた状態から手を離すとき、棒が手に僅かながら仕事をしてエネルギーを失うこともやはり不可避、ということになる。
上の議論では簡単のため「棒は左右対称」「散逸によって手を離した後の棒の振動はやがて収まる」と仮定したが、そのことは「相対論では、棒が手に対して仕事ができないくらい素早く手を離すことは不可能」という議論の成立には影響を与えないはずだ。左端で手が今正に離れつつある場所・瞬間の分子・原子たちに右端での出来事が完全に左右対称かどうかなどということは知りようもないことだし、「後に散逸によって振動が収まるかどうか」というのもその局所的なプロセスのありようには影響しようのないことだろう。
元記事の blog は新しい場所に移行しているが、そこでの続きの記事
極端大仏率StrikesBack “「『相対性理論はやはり間違っていた!』はやはり間違っていた!」は間違っていたのか?”
のコメント欄で次のような疑問が提示されている。
“質点の質量というのが静止質量を意味するのと同じく、棒の質量というときは、伴走系であるSで測った値を使うことになります。すると、両手は仕事をしていないので、棒のエネルギーに変化はありません。従って質量の変化もありません。”
や
“Sから見て、棒を離す前に、充分な時間、両手が静止していた場合は、両手が仕事をしていないので、棒のエネルギー変化はあり得ないのではないか?(もちろん、手を離した後は外力がなくなるので、エネルギー変化はない)”
等である。これらには当該記事およびそのコメントでは回答が与えられていないが、おそらく上の私の考察がその疑問の答になっているのではないだろうか。つまり、この質問者が想定しているのは「\(S\) 系で手は棒に仕事しない(棒も手に仕事をしない)場合がありえて、その場合は \(S\) 系で棒のエネルギーは変化しない」ということなのだが、そういう状況は実際には起こらず、「どのような舞台設定を整えようとも、\(S\) 系で必ず棒のエネルギーは変化(減少)してしまう」というのが相対論という枠組によって要請される理論的制限なのだと思う。
直角レバーのパラドックス
先ほどのパラドックスを知ったのはかなり以前のことだったが、次のものは今年の8月末に知ったばかりだ。
“直角レバーのパラドックス”
注意してほしいが、途中にちょっと出てくる「天秤に \(2\) つの力をかけ、一方の作用点を時間と共に動かしていく」話の方は全然パラドックスになっていない(この配置だと、下向きのふたつの力の作用点を直線で結んで真上から見下ろしたとき、直線と天秤の支点が重なって見えないので、(どちらの慣性系かに関係なく)天秤が水平を保たないのは当たり前だ。相対論を持ち出すまでもなく Newton 力学の段階で傾く(どちらの系でも)、ということになって何の矛盾もない。)。その後で論じられている「直角に曲がったレバーに回転軸回りの逆向きの力を与える」話の方が本題だ。「静止系から見るとレバーに加えられる正味のトルクは \(0\) でレバーは静止しているのに、運動系から見ると正味のトルクは \(0\) でない。ということは、運動系ではレバーは回らないとおかしい。いったい、レバーは回るのか、回らないのか?」というパラドックスで、これも(私にとっては)非常に刺激的だった。解決策を考えている過程はとても興奮に満ちていて、数日間たっぷり楽しめた。さらに、その時ひねり出した解決策には不十分な所があって、その説明だと今度はまた新たなパラドックスができてしまうということにこの記事を書いている最中に気づき、そこを乗り越えるためにまた丸2日ほどかかってしまう、という情けない体たらくだった。
概ね事情がわかった所で以下の解説記事を手がかりに調べてみると、
http://www.mathpages.com/home/kmath651/kmath651.htm
https://arxiv.org/abs/1206.4487v1
これは20世紀初頭に相対論が提唱されて徐々に受容されていくなかで論じられたパラドックスで、その過程で解決策が見つかったものだそうだ。上で論じた極端大仏率のパラドックス(という名前でいいかどうかはわからないけど)と同じく「相対論の正しい間違え方」に載っていないという意味では「ド定番」ではないだろう。内山龍雄が訳したパウリの教科書にも関連する話題が載っていたが、あまり踏み込んだ形でパラドックスを解決する内容にはなっておらず、多くの人に忘れられた(少なくとも、日本では)話題になってしまい、日本では上掲のように相対論否定者による記事くらいしか見つからない、という状況になってしまったようだ。とは言え、初出から100年以上経過した由緒正しい「大物」のパラドックスなわけだから、それをこれまで知らないでいたとはお恥ずかしい。(もっとも、これも物理に強そうな職場の方数人に聞いてみたところ、やはり皆初耳という感じの反応ではあったのだが)
私が(自分にとって)納得できる解決に至ったのは、「そもそも、角運動量とトルクの関係ってどうなってたんだっけ。何がどうなると保存して、どういう時に角運動量の時間微分がトルクに一致するんだっけか?」ということを基本に立ち返って考えて確認し直して初めて可能なことだった。以下、私の理解した内容を整理して書いていこうと思う。
まず、一番簡単なケースで角運動量の定義とトルクの関係から復習しよう。質点 \(1\) 個に外力 \(\V{F}\) が働く力学系では、運動量を \(\V{p}\) とすれば運動方程式は
\begin{equation}
\label{eq:relativity-paradox-1}
\frac{d}{dt}\V{p} = \V{F}
\end{equation}
であり、角運動量 \(\V{L}\) は
\[ \V{L} = \V{r} \times \V{p} \]
と定義される。これらは Newton 力学でも特殊相対論でも変わらない。
\(\V{L}\) の時間微分を計算してみよう。
\begin{align}
\frac{d}{dt}\V{L} &= \frac{d}{dt} (\V{r} \times \V{p}) \notag\\
&= \frac{d\V{r}}{dt} \times \V{p} + \V{r} \times \frac{d\V{p}}{dt} \notag\\
\label{eq:relativity-paradox-2}
&= \V{v} \times \V{p} + \V{r} \times \V{F} \quad (\because
\eqref{eq:relativity-paradox-1})
\end{align}
ここで、Newton 力学でも特殊相対論でも速度 \(\V{v}\) が運動量 \(\V{p}\) と平行なのは変わらないので、\eqref{eq:relativity-paradox-2}の第 \(1\) 項 \(\V{v} \times \V{p}\) は \(\V{0}\) になって消える。よって\eqref{eq:relativity-paradox-2}より
\begin{equation}
\label{eq:relativity-paradox-3}
\frac{d}{dt}\V{L} = \V{r} \times \V{F}
\end{equation}
である。トルク \(\V{\tau}\) を \(\V{\tau} = \V{r} \times \V{F}\) によって定義すれば、\eqref{eq:relativity-paradox-3}は「角運動量の時間微分はトルクに等しい」と言い換えられる式だ。
このように、角運動量とトルクの関係は、角運動量の定義と運動方程式から単純計算で容易に導ける。多体系になったり、別の慣性系にうつったときにどういう関係で結ばれているかを考えたりしていくと式も複雑になっていくが、根本にあるのが上のようなシンプルな関係であることは変わらない。なので、そこさえ見失わなければ誰でも理解できるはずだ。
\eqref{eq:relativity-paradox-3}より「角運動量が保存する条件は、トルクが \(\V{0}\) になること」という法則が得られる。その代表的な例が、質点にはたらく力 \(\V{F}\) が「中心力」の場合で、原点をその中心に取れば \(\V{r} \parallel \V{F}\) となって \(\V{\tau}\) が消え、\(\V{L}\) が時間変化しなくなる。例えば Newton 力学での太陽系の惑星の運動などが典型的な例だ。
ここで、角運動量とトルクに関する、次の \(2\) 点に注意を喚起しておく。
まず、運動方程式を\eqref{eq:relativity-paradox-1}としたことから、\(\V{F}\) は質点にはたらいているすべての力の合力である。つまり、トルク \(\V{\tau}\) を求める場合は、質点にはたらくすべての力 \(\V{F}_{1}, \V{F}_{2}, \dotsc\) をリストアップし、その合力 \(\V{F} = \V{F}_{1} + \V{F}_{2} + \dotsb\) によるトルクを計算しなければならない。あるいは、
\[ \V{r} \times (\V{F}_{1} + \V{F}_{2} + \dotsb) = \V{r} \times \V{F}_{1}
+ \V{r} \times \V{F}_{2} + \dotsb \]
なので、個々のトルク \(\V{r}\times \V{F}_{1}, \V{r} \times \V{F}_{2}, \dotsc\) を合計してもよいが、いずれにせよ力やトルクはすべてを合算しなければならない。力の一部だけ取り出してしまうと「角運動量の時間微分はトルクに等しい」という関係が成立しなくなってしまうことに注意しておく。
第2に、角運動量とトルクの定義式
\begin{equation}
\begin{split}
\V{L} &= \V{r} \times \V{p} \\
\V{\tau} &= \V{r} \times \V{F}
\end{split}
\label{eq:relativity-paradox-4}
\end{equation}
に質点の位置ベクトル \(\V{r}\) が生で現れていることからもわかる通り、\(\V{L}\) や \(\V{\tau}\) は原点の取り方に依存する量である(このことは、上の中心力の話で原点を中心力の中心点に取り直していた所にも顔を覗かせている)。つまり、角運動量(トルク)というのは、もともと「どの点の周りの」角運動量(トルク)を考えているのか、ということを明確にしないと意味を持たない量だ。基準にする点の取り方を変えると角運動量(トルク)の値も変わる。どのように変わるのか押さえておこう。
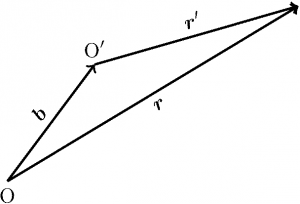
図のように、基準点を \(\text{O}\) から \(\text{O}’\) に取り直した時に、質点の位置ベクトルが \(\V{r}\) から \(\V{r}’\) に変化するとする。\(\overrightarrow{\text{OO}’} = \V{b}\) とすると \(\V{r}’ = \V{r} – \V{b}\) なので、\(\text{O}’\) の周りの角運動量 \(\V{L}’\) は
\begin{align}
\V{L}’ &= \V{r}’ \times \V{p}’ = (\V{r} – \V{b}) \times \V{p}
\quad (\because \V{p}’=\V{p}) \notag\\
&= \V{r} \times \V{p} – \V{b} \times \V{p} \notag\\
\label{eq:relativity-paradox-6}
&= \V{L} – \V{b} \times \V{p}
\end{align}
となる。同様に、\(\text{O}’\) の周りのトルク \(\V{\tau}’\) は
\begin{align}
\V{\tau}’ &= \V{r}’ \times \V{F}’ = (\V{r} – \V{b}) \times \V{F}
\quad (\because \V{F}’=\V{F}) \notag\\
&= \V{r} \times \V{F} – \V{b} \times \V{F} \notag\\
\label{eq:relativity-paradox-7}
&= \V{\tau} – \V{b} \times \V{F}
\end{align}
となっている。
当然ながら基準点を取り替えても「角運動量の時間微分はトルクに等しい」という法則はそのまま成立し、
\[ \frac{d}{dt} \V{L}’ = \V{\tau}’ \]
がなりたつ。ここで大切なことは、\(\V{b}\) が時間によらないこと、つまり\(\text{O}’\) が定点であることが暗黙のうちに仮定されていることだ。これは角運動量やトルクの定義から当然である。もともと、角運動量やトルクを\eqref{eq:relativity-paradox-4}のように定義した時の基準点は、考えている慣性系の座標原点を採用しているわけだから、「角運動量やトルクの基準点は、慣性系での定点を採用する」という決まりがそれらの定義に最初から入っているということになる。
なお、トルクについては基準点の取り方を気にしなくていい場合がある。全合力 \(\V{F}\) が \(\V{0}\) の場合がそれで、\eqref{eq:relativity-paradox-7}で \(\V{b} \times \V{F} = \V{0}\) となるため \(\V{\tau}’ = \V{\tau}\) がなりたつ。この場合、「全トルクを計算する」目的のためだけなら、定点ではない点を基準点にしても計算結果に変わりはない(と言っても、全角運動量の方はそういうわけにはいかない)。
続いて、多体系の考察にうつる。複数の質点に番号を振っておき、それを添字 \(i\) で表すことにする。個々の質点の運動量を \(\V{p}_{i}\)、働く力を \(\V{F}_{i}\) とすると、運動方程式は
\[ \frac{d}{dt} \V{p}_{i} = \V{F}_{i} \]
となる。それぞれの角運動量 \(\V{L}_{i} = \V{r}_{i} \times \V{p}_{i}\) の総和
\[ \V{L} = \sum_{i} \V{r}_{i} \times \V{p}_{i} \]
を \(t\) で微分してみると
\begin{align*}
\frac{d}{dt} \V{L} &= \sum_{i} \Bigl( \frac{d\V{r}_{i}}{dt} \times
\V{p}_{i} + \V{r}_{i} \times \frac{d}{dt} \V{p}_{i}
\Bigr) \notag\\
&= \sum_{i} \Bigl( \underbrace{\V{v}_{i} \times
\V{p}_{i}}_{\text{$\V{v}_{i} \parallel \V{p}_{i}$より$\V{0}$}} +
\V{r}_{i} \times \V{F}_{i} \Bigr) \notag\\
&= \sum_{i} \V{r}_{i} \times \V{F}_{i}
\end{align*}
となって、それぞれにはたらくトルク \(\V{\tau}_{i} = \V{r}_{i} \times \V{F}_{i}\) の総和になっている。すなわち、角運動量・トルクは共に加法的な量で、多体系の場合は各質点に対する量を単純に足し合わせたものを系全体の量とすればいい、ということがわかる。式で書けば、全角運動量 \(\V{L} = \sum_{i} \V{L}_{i}\) と全トルク \(\V{\tau} = \sum_{i} \V{\tau}_{i}\) は
\begin{equation}
\label{eq:relativity-paradox-5}
\frac{d}{dt} \V{L} = \V{\tau}
\end{equation}
という\eqref{eq:relativity-paradox-3}を自然に拡張した関係をみたす。
多体系になっても、角運動量やトルクは「どの点の周りの」量なのかを指定しないと意味がない量であることは変わらない。さらに、上の式の中でも自然に前提として入り込んでいるが、全角運動量や全トルクを求める際、その基準点はすべての質点に共通に取る。そしてまた、基準点は慣性系での定点に取らなければならない。
ただし、多体系の場合も、全合力が \(\V{0}\) になる場合は全トルク \(\V{\tau}\) が基準点の取り方によらないことは変わりない。実際、基準点を\(\V{b}\) に取り替えた場合、\eqref{eq:relativity-paradox-7}によって各質点に対するトルクは \(\V{\tau}’_{i} = \V{\tau}_{i} – \V{b} \times \V{F}_{i}\) になるから、全トルク \(\V{\tau}’\) は
\begin{align*}
\V{\tau}’ &= \sum_{i} \V{\tau}’_{i} \\
&= \sum_{i} (\V{\tau}_{i} – \V{b} \times \V{F}_{i}) \\
&= \V{\tau} – \V{b} \times \sum_{i} \V{F}_{i}
\end{align*}
となって、全合力 \(\sum_{i} \V{F}_{i}\) が \(\V{0}\) なら \(\V{\tau}’ = \V{\tau}\) となって全トルクは不変である(もちろんこの場合も、基準点 \(\V{b}\) は全質点に対して共通に取らなければいけないことは変わりない)。
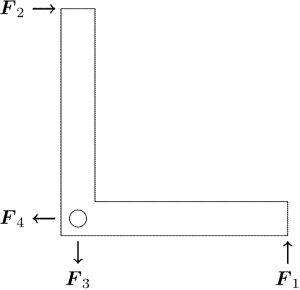
さて、いよいよ直角レバーのパラドックスの分析に入ろう。上の多体系の議論が使えるように、レバーは無数の微小な質量素片の集まりとして解析する。最初はどちらの慣性系でも変わらず成立する話から入る。上で注意した通り、系にはたらく全トルクを考える場合は、各素片にはたらくすべての力を計算に入れなければならない。まず、レバーにはたらく力として、元々の力 \(\V{F}_{1}, \V{F}_{2}\) 以外に、それらの抗力として支点から与えられる \(\V{F}_{3}, \V{F}_{4}\) がある。抗力はレバー全体としての加速度が発生しないように供給されるから \(\V{F}_{3} =-\V{F}_{1}\), \(\V{F}_{4}=-\V{F}_{2}\) で、これらの全合力 \(\V{F}_{1} + \V{F}_{2} + \V{F}_{3} + \V{F}_{4}\) は消える。
上で注意した通り、トルクを考える場合は質点にはたらく「すべての」力を考えに入れなければならなかったので、考えるべき力は \(\V{F}_{1}\)〜\(\V{F}_{4}\) だけでは不十分だ。これらは多体系の外部から与えられる力(外力)だが、それら以外に、素片どうしが及ぼし合う力(内力)も考えなければいけない。レバーを構成する無数の素片に番号を振り、\(i\) 番目の素片にはたらく外力を \(\V{f}_{i}\), \(i\) 番目の素片に \(j\) 番目の素片が及ぼす内力を \(\V{f}_{ij}\) と書こう。大半の素片に対しては外力 \(\V{f}_{i}\) は \(\V{0}\) で、\(\V{F}_{1}\)〜\(\V{F}_{4}\) の作用点の素片に対してのみ \(\V{f}_{i} \ne \V{0}\) となる。
すると \(i\) 番目の素片にはたらく力は \(\V{f}_{i} + \sum_{j} \V{f}_{ij}\) だから、トルクは
\[ \V{\tau}_{i} = \V{r}_{i} \times \V{f}_{i} + \sum_{j} \V{r}_{i} \times \V{f}_{ij} \]
となる。よって、\eqref{eq:relativity-paradox-5}より
\begin{align}
\frac{d}{dt} \V{L} &= \sum_{i} \V{\tau}_{i} \notag\\
\label{eq:relativity-paradox-10}
&= \underbrace{\sum_{i} \V{r}_{i} \times \V{f}_{i}}_{\text{外力による全トルク}} + \underbrace{\sum_{i,j} \V{r}_{i} \times \V{f}_{ij}}_{\text{内力による全トルク}}
\end{align}
となる。このうち第 \(2\) 項の「内力による全トルク」は式変形を進める余地がまだ残っている。この被積分関数ならぬ「被和項」は \(i\), \(j\) に関する対称性が低いが、作用・反作用の法則 \(\V{f}_{ij} = -\V{f}_{ji}\) を利用すると
\[ \sum_{i,j} \V{r}_{i} \times \V{f}_{ij} = \sum_{i<j} (\V{r}_{i} – \V{r}_{j}) \times \V{f}_{ij} \]
と書き直せる。よって\eqref{eq:relativity-paradox-10}は結局
\begin{equation}
\label{eq:relativity-paradox-12}
\frac{d}{dt} \V{L} = \sum_{i} \V{r}_{i} \times \V{f}_{i} + \sum_{i<j}
(\V{r}_{i} – \V{r}_{j}) \times \V{f}_{ij}
\end{equation}
とまとめられる。
\eqref{eq:relativity-paradox-12}の左辺が \(\V{0}\) であることはすぐわかる。まず、レバーが静止する慣性系 \(K\) ではすべての微小素片の速度が \(\V{0}\) なので運動量も \(\V{0}\)、よって角運動量も \(\V{0}\) でその総和も \(\V{L}=\V{0}\) である。また、レバーが動いて見える慣性系 \(K’\) では、すべての微小素片の速度 \(d\V{r}_{i}/dt = \V{v}_{i}\) が \(K\) と \(K’\) の相対速度 \(\V{u}\) と一致し、微小質量 \(m_{i}\) も時間によらず一定なので運動量 \(\V{p}_{i}\) は \(\V{u}\) と平行かつ一定。したがって
\[ \frac{d}{dt}(\V{r}_{i} \times \V{p}_{i}) = \V{u} \times \V{p}_{i} +
\V{r_{i}} \times \frac{d}{dt}\V{p}_{i} = \V{0} \]
で、その総和 \(d\V{L}/dt\) も \(\V{0}\)。(なお、上で挙げたページ
http://www7b.biglobe.ne.jp/~kcy05t/nirigha.html
では途中で \(K\) と \(K’\) の立場が入れ替わってしまって紛らわしいが、本記事では一貫して \(K\) は「レバーが静止して見える慣性系」、\(K’\) は「レバーが動いて見える慣性系」を表すとする)
続いて\eqref{eq:relativity-paradox-12}の右辺を調べる。まず第 \(1\) 項は外力によるトルクの総和である。外力の全合力 \(\V{F}_{1} + \V{F}_{2} + \V{F}_{3} + \V{F}_{4}\) が \(\V{0}\) だったから、外力による全トルクは基準点の取り方によらない。そこでレバーの支点を基準点にとると、抗力 \(\V{F}_{3}\), \(\V{F}_{4}\) のトルクへの寄与はなくなるので、結局 \(\V{F}_{1}\), \(\V{F}_{2}\) からの寄与のみを考えればよくなる。そうやって計算すると、外力による全トルクの大きさは、慣性系 \(K\) では \(0\) となるが、\(K’\) では上掲の参照ページでの計算通り \(F \ell (u/c)^{2} \ne 0\) となる(\(F\) は \(K\) での力 \(\V{F}_{1}\), \(\V{F}_{2}\) の共通の大きさ、\(\ell\) は \(K\) でのレバーの腕の長さ、\(u/c\) は \(K\) と \(K’\) の相対速度 \(\V{u}\) の光速に対する比)。
問題は、\eqref{eq:relativity-paradox-12}の右辺第 \(2\) 項、内力による全トルクの項である。この項が \(K’\) で消えるならば確かに\eqref{eq:relativity-paradox-12}で等号がなりたたなくなって矛盾が生じることになる。詳しく調べてみよう。もしも
☆2つの(微小な)物体どうしの作用・反作用は、常に物体同士を結ぶ直線に沿った方向にはたらく
という法則がなりたつなら、\(\V{f}_{ij} \parallel \V{r}_{i} – \V{r}_{j}\) によって \((\V{r}_{i} – \V{r}_{j}) \times \V{f}_{ij} = \V{0}\) となり、内力による全トルクは消え、
★全角運動量の時間微分は、外力による全トルクに等しい(内力のことは考えなくていい)
という関係がなりたつことになる。そうなると、\(K’\) 系ではパラドックスが順調に(?)生じる。
しかし、法則☆は果たして本当になりたつのだろうか。「なりたつに決まってる。だってそれは作用・反作用の法則に含まれるじゃないか」という方もいるだろう。実際、力学の教科書によっては作用・反作用の法則にそれを含める流儀のものもあるし、特に Newton 力学で剛体を取り扱う場合には通常☆を仮定する(そのため、★に基づいて運動が解析できるようになる)。ところが、今から説明する通り、☆は相対論的効果を無視しない場合には成立しなくなる。
http://www.mathpages.com/home/kmath651/kmath651.htm
の中ほどの、2つの負電荷が外力を与えられて釣り合っているケースの考察でも出ているように、ある慣性系では作用・反作用が質点同士を結ぶ直線に沿ってはたらいていたとしても、その直線に対して斜めの速度を持つ別の慣性系では、Lorentz 変換によって作用・反作用は質点同士を結ぶ直線からずれた向きにはたらく(その場合も、外力もふくめすべて Lorentz 変換されるので、各電荷にはたらく力は釣り合っていて矛盾は発生しない。このように、相対論では作用・反作用の法則は「作用と反作用は大きさが等しく向きが反対のベクトルになる」という部分までしか保証されず、☆は慣性系ごとになりたったりなりたたなかったりする)。
Newton 力学では力という量は慣性系の取り方によらないから、☆は慣性系の対等性と両立する。すなわち、ひとつの慣性系で☆がなりたつなら、他のすべての慣性系でも☆が保証され、矛盾は発生しない。したがって、Newton 力学では☆を慣性系非依存な普遍法則として要請することができる。一方、相対論になるとそうは言えず、☆は普遍法則たりえない(あるひとつの慣性系で☆がなりたっていたとしても、他の慣性系ではまったくなりたたなくなる)。
したがって、相対論では一般には外積 \((\V{r}_{i}-\V{r}_{j}) \times \V{f}_{ij}\) は \(\V{0}\) にならず、内力による全トルクが消えないことがありうる。つまり、相対論的効果を無視して力が慣性系によらないと見なせる間は☆を仮定してよいのだが、本件のように Lorentz 変換による力の変化を考えに入れる場合はそうは行かず、☆も★も仮定できない(つまり、多体系での最も一般的な場合を考えると、場所によって☆がなりたつかどうかの差が出てくるだろう。この場所では☆は(ほぼ)なりたっているけど、別の場所では全然成立しない、という具合に。そうなると、☆が系全体に渡っていい近似で成立するような慣性系は存在しない、ということもありえておかしくない。上述の通り、普通の Newton 力学での多体系では☆の成立(とその帰結としての★)を前提とするわけだが、それは Newton 力学を相対論の近似理論と見る立場では「☆が系全体に渡っていい近似で成立する。そういう慣性系が存在する系だけを考察対象とする」という仮定を置いていることに当たるだろう)。このため \(K’\) では\eqref{eq:relativity-paradox-12}右辺第 \(2\) 項は消えずに残り、それがちょうど\eqref{eq:relativity-paradox-12}の右辺第 \(1\) 項の、大きさ \(F \ell (u/c)^{2}\) のベクトルと打ち消しあって、\eqref{eq:relativity-paradox-12}の右辺全体としてはやっぱり \(\V{0}\) になっているのだ。これで左辺が \(\V{0}\) になることと矛盾しなくなり、パラドックスは解消される。
\begin{align*}
\text{$K$では:}& \underbrace{\frac{d \V{L}}{dt}}_{\V{0}} =
\underbrace{\sum_{i} \V{r}_{i} \times
\V{f}_{i}}_{\V{0}} +
\underbrace{\sum_{i<j} (\V{r}_{i} – \V{r}_{j}) \times
\V{f}_{ij}}_{\V{0}} \\
\text{$K’$では:}& \underbrace{\frac{d \V{L}}{dt}}_{\V{0}} =
\underbrace{\underbrace{\sum_{i} \V{r}_{i} \times
\V{f}_{i}}_{\text{大きさ}F\ell(u/c)^{2}} +
\underbrace{\sum_{i<j} (\V{r}_{i} – \V{r}_{j}) \times
\V{f}_{ij}}_{\text{第1項と反対向きで同じ大きさ}}}_{\text{打ち消し合って}\V{0}}
\end{align*}
したがって、
http://www7b.biglobe.ne.jp/~kcy05t/nirigha.html
の
“観測者が動きだした途端に、触れずしてこのレバーは回転し始めることになる(= Fig.5 右)。これは明らかに致命的なパラドックスであり、特殊相対論が間違いであることを示している。”
や
“結果的に、移動する観測者の視点のみで、レバーの回転トルクはゼロにならないことになる。静止した観測者からはレバーのトルクはゼロなのにである。これは明らかなパラドックスである。”
という主張は成立しない。確かに、慣性系 \(K’\) では外力による全トルクはゼロにならないが、それはレバーが回転し始めることと直結しない。そのトルクはあくまで「外力の」全トルクであって、内力によるトルクが考慮されていない。今の場合、☆や★が成立しないため内力による全トルクは消えないから、\(K’\) でも全角運動量は保存し、レバーは回転しないまま等速直線運動を続ける、としても何も矛盾は発生しない。
(なお、作用・反作用の法則に関しては、そもそも「作用・反作用は大きさが同じで向きが反対の力になる」という部分に限ってさえも、2つの質点が電磁場を介して力を伝えあうときは成立するとは限らない(例えば、Feynman 物理学のII巻26-2
http://www.feynmanlectures.caltech.edu/II_26.html#Ch26-S2
(日本語訳だとIV巻5-2)の最後に、そういう例がある。それでいながらI巻18-4
http://www.feynmanlectures.caltech.edu/I_18.html#Ch18-S4
でシレッと“not simply that the action and reaction are equal, but also that they are directed exactly oppositely along the same line”と言ってるんだから、Feynman さん人が悪い(笑)。なおここは日本語訳(やはりI巻18-4)だと along the same line「同一直線上で」という限定が落ちてしまってただの“作用と反作用は同じ方向でむきが正反対である”になっちゃってますね…)。
つまり、「作用・反作用は大きさが同じで向きが反対の力になる」というのは、力が瞬時に離れた物体にも伝わるような遠隔力と見なせるスケールで考えている間しか正しくなく、電磁場(のような場)が力を(有限の時間をかけて)媒介する場合は、場の運動量も含めた全運動量の保存、という形に拡張した法則に書き直さないと成立しなくなるのだ(それが相対論でのエネルギー運動量テンソルに対する保存則 \(\nabla_{\mu} T^{\mu\nu}=0\) (のうち、空間成分)である)。そういう意味で、力学の入門時に習う Newton の運動法則のうち、第3法則は実は適用限界のある近似法則に過ぎない(相対論や量子論を考えない古典物理の範囲でも)という点は注意が必要だ)
さて、この「直角レバーのパラドックス」は、
http://www.mathpages.com/home/kmath651/kmath651.htm
でより掘り下げた説明が与えられている。そこでは“more profound explanation was given by von Laue in 1911”と評されているが、確かに質量とエネルギーの等価性、「エネルギー流ある所運動量密度あり」という相対論の根本原理を見事に捉えた説明だ(ラウエという名前は私は「ラウエ斑点」でくらいでしか知らなかったんですが、こうやって初期相対論の建設でも重要な役割を果たしていたんですね!)。レバーが変形しないのはレバー内部の応力(内力)が外力に逆らってレバーを支えているためだが、こういう内部応力がある場合は、相対論では物体のエネルギーや運動量への追加の寄与があり、それに由来する追加の角運動量も含めれば、それがちょうど今の場合の正味の外力全トルク \(F\ell(u/c)^{2}\) に見合う分量になっている…というのがその説明の概要だ。
この「相対論では内部応力が追加のエネルギーや運動量に寄与する」ということをもう少し詳しく説明しよう。例えば
http://www.mathpages.com/home/kmath651/kmath651.htm
の中程で \(3\) つの電荷が直角をなすよう配置された図を見てみよう(その図は電荷の大きさがおかしくて、斜め方向の力の大きさを図の通り \(\sqrt{2}F\) にするためには \(2\) つの正電荷の大きさを \(\sqrt{2}\) ではなく \(2\sqrt{2}\) にしなければいけないはずだが、その辺りは適宜修正して見て欲しい)。これは直角レバーに力が加わって釣り合っている状況を模しており、電荷を押す外力に対して電磁気力が「内部応力」の役割を果たして全体が釣り合っている…という状況である。ここでは、各電荷が元々持っている質量(エネルギー)に加えて電磁場のエネルギーも存在するし、運動系で見たら \(\V{E}\) も \(\V{B}\) も両方あるので Poynting vector \(\V{S} = \V{E} \times \V{B}\) による電磁場の運動量もある。これらが「内部応力が担うエネルギー・運動量」に相当する。これらと、元々の電荷のエネルギー・運動量を合わせたものが系全体のエネルギー・運動量だ。
直角レバーの内部応力のモデルとしてもっと複雑なものも考えることができるが、それらはすべて電磁場ではないにしろ何らかの物質が内力の源になるしかないはずで(※ ここでは電磁場のような場も含めて物質と呼んでいる)、そうやって何らかの物質がある以上そこにはその物質自身のエネルギー・運動量が必ず伴わなければならない(相対論は光速度不変性や慣性系の相対性に加えてエネルギー・運動量保存則を基本原理として採用しているが、それをみたすためには「どのように力や仕事を与え・与えられる物質であっても、必ずエネルギー・運動量を持つ」ことが必須条件として要請される)。したがって、相対論的には内力があれば必ずそれに伴うエネルギー・運動量が発生することになる。
このことは上の「極端大仏率のパラドックス」でも示唆されていた(両端を押さえている間と離した後では棒のエネルギーに変化があったが、これは押さえている間に棒の内部に存在している圧力がエネルギーに寄与しているという見方ができる)。あるいはエネルギー運動量テンソルの空間成分 \(T^{ij}\) は応力テンソルを拡張したものになっていることからも、内部応力がある場合はそれに物体のエネルギー・運動量が伴うということが読み取れる。
ラウエの議論は定量的評価も行っており、その計算も
http://www.mathpages.com/home/kmath651/kmath651.htm
に載っている。その考察の核心は「レバーが動いて見える慣性系では、レバー内にはエネルギーの流束が生ずる」という話なのだが、私はこの話には馴染みがなく、初読では「おお、何かいかにもそれっぽいカッコイイ感じの話が出てきたな」とは感じたものの、そんなものが発生するすっきりした説明が浮かばずもどかしい思いをした。その後あれこれ考えた結果、「うん、確かにそういうものは存在するはずだ」という事情が掴めた(こういう、よく知っているはずの分野にも時々思いがけない気づきがあるから数学や理論物理は面白い♪)ので、私と同様にピンと来なかった方のために説明を試みる。
まずは、運動方程式に基づいて仕事とエネルギーの関係を再確認してみよう。簡単のため、一粒子系の場合の式で説明するが、多体系でも話はまったく同様だ。
運動方程式は Newton 力学でも特殊相対論でも
\[ \frac{d}{dt} \V{p} = \V{F} \]
の形をとるが、この両辺に速度 \(\V{v}\) を内積すると
\begin{equation}
\label{eq:relativity-paradox-14}
\V{v} \cdot \frac{d}{dt} \V{p} = \V{F} \cdot \V{v}
\end{equation}
である。ここで、\(\V{p}\) と \(\V{v}\) の関係は、Newton 力学では \(\V{p}=m\V{v}\), 特殊相対論では \(\V{p} = m\V{v}/\sqrt{1-(v/c)^{2}}\) だから、\eqref{eq:relativity-paradox-14}の左辺はそれぞれ次のように書き直せる。
\[ \V{v} \cdot \frac{d}{dt} \V{p} =
\left\{
\begin{aligned}
\frac{d}{dt} \biggl( \frac{1}{2}m v^{2} \biggr) & \quad \text{(Newton
力学の場合)} \\
\frac{d}{dt} \frac{mc^{2}}{\sqrt{1-(v/c)^{2}}} & \quad \text{(特殊相対論の場合)}
\end{aligned}
\right. \]
つまり\eqref{eq:relativity-paradox-14}の左辺は、いずれの場合も「エネルギーの時間微分」である。ここで「エネルギー」というのは Newton 力学の場合は運動エネルギー \(mv^{2}/2\)、特殊相対論の場合は質量エネルギー \(mc^{2}/\sqrt{1-(v/c)^{2}}\) で、これらを \(E\) と書けば、\eqref{eq:relativity-paradox-14}の両辺を短い時間間隔 \(\Delta t\) にわたって \(t\) で積分したものは
\begin{equation}
\label{eq:relativity-paradox-15}
\Delta E = \V{F} \cdot \V{v} \Delta t
\end{equation}
となる。ここで、左辺 \(\Delta E\) は微小時間 \(\Delta t\) の間の \(E\) の変化量、右辺に現れる \(\V{v} \Delta t\) はその間の微小変位だから、\eqref{eq:relativity-paradox-15}は
エネルギー \(E\) の時間変化は、その間に力 \(\V{F}\) から受ける仕事に等しい
という法則を表す。別の言い方をすれば、力 \(\V{F}\) からは毎秒 \(\V{F} \cdot \V{v}\) のエネルギーが流入する、ということだ(内積の値が負の場合は流出)。
ここで、\(\V{F}\) は物体にはたらくすべての力の合力だが、複数の力がはたらいている場合は \(\V{F} = \V{F}_{1} + \V{F}_{2} + \dotsb\) を代入すると、
\[ \V{F} \cdot \V{v} = \V{F}_{1} \cdot \V{v} + \V{F}_{2} \cdot \V{v} +
\dotsb \]
となるので、各々の力 \(\V{F}_{1}, \V{F}_{2}, \dotsc\) から別々にエネルギーの流入があると思って、それらを単純に合計すれば、物体が得る正味のエネルギーが得られる。
以上の確認を踏まえて、仕事によりエネルギー流束が発生する具体例を見てみよう。
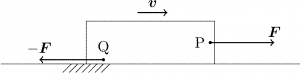
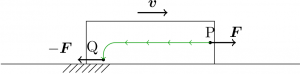
図のように、摩擦がある水平な床で、荷物を横に引っ張っており、引く力 \(\V{F}\) と動摩擦力 \(-\V{F}\) が釣り合って荷物が一定速度 \(\V{v}\) で動いているとする。このとき、引く力 \(\V{F}\) の作用点 P では毎秒 \(\V{F} \cdot \V{v}\) のエネルギーが流入しており、摩擦力 \(-\V{F}\) の作用点 Q では毎秒 \(-\V{F} \cdot \V{v}\) の流出がある。それらが打ち消し合うので、荷物の持つエネルギー \(mv^{2}/2\) の正味の増減はない。P で注入されたエネルギーは、最終的に Q で吸い出されて摩擦熱に転化しているわけだ。
エネルギーが注入されている点 P と吸い出されている点 Q が離れているわけだから、P から Q まではエネルギーが「運ばれて」いるはずだ。つまり荷物の中にはエネルギーの流れ(流束)が発生していることになる。これは、荷物を細かく分割してみるとよりはっきりするだろう。
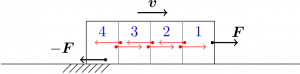
荷物を図のような微小要素に分割すると、内部応力としての張力が赤の矢印のように可視化される。各微小要素には青で番号を振っておいた。まず右端の微小要素1に着目すると、元々の引っ張る力 \(\V{F}\) によって毎秒 \(\V{F} \cdot \V{v}\) のエネルギーが流入し、それと同量のエネルギーが隣の要素2からはたらく左向きの張力(大きさは \(\V{F}\) と同じ)によって吸い出されている。吸い出されたエネルギーは、要素2を要素1が引く張力によって要素2に流れ込み、要素3が要素2を引く張力によって吸い出されている。
これの繰り返しでエネルギーは要素2から要素3へ、要素3から要素4へと流れていき、要素4にはたらく摩擦力 \(-\V{F}\) によって吸い出される。吸い出されたエネルギーはもう行き場がない(床は静止していて仕事を受けないので、床に対してはエネルギーの流入も流出もない)ので、その場で摩擦熱として顕在化するしかない。このようにして、荷物の内部には次の図の緑のように、P から Q まで続くエネルギーの流束が生じる。
同様に、物体に複数の力がはたらいていて、それらから受ける仕事の符号が異なっている場合、物体内部にエネルギーの流束が発生するというのは Newton 力学のレベルで十分理解できる話であることがわかるだろう。
注意しなければいけないのは、エネルギー流束の有無は慣性系の取り方によって変わるということだ。上の例は暗黙のうちに床に対して静止する慣性系で考えていたが、もし床に対して速度 \(\V{v}\) で動く慣性系を取れば、荷物が静止していて、床が速度 \(-\V{v}\) で動いていく。荷物は仕事を受けず、エネルギーの流入も流出もないので、エネルギー流束もない。代わりに、床が荷物からの右向きの摩擦力と地球からの左向きの抗力を受けながら運動しているので、床の内部にエネルギー流束が現れ、やはり摩擦点から吸い出されたエネルギーが摩擦熱になっている。
慣性系の取り方を変えただけでエネルギー流束が消えたり現れたりするというのは奇異に感じる人もいるかもしれないが、そんなことはまったくない。ごく普通の単一粒子の運動エネルギーでも、粒子と同じ速度の慣性系では \(0\) で、それ以外の慣性系では \(>0\) となるわけで、エネルギーの有無が慣性系によって変わるなんてことは何の変哲もないありきたりのことだ。
今の知見を直角レバーのパラドックスの考察に生かそう。レバーが右に速度 \(\V{u}\) で動く慣性系で見ると、力 \(\V{F}_{2}\) によってエネルギーが注入され、\(\V{F}_{4}\) によって抜き出されているとわかる(力 \(\V{F}_{1},
\V{F}_{3}\) は \(\V{u}\) と垂直で仕事をしておらず、エネルギーの流入・流出には関与しない)。したがってレバー内部には、\(\V{F}_{2}\) の作用点から \(\V{F}_{4}\) の作用点までのエネルギー流束がある。すると、相対論の基本原理によってこれは運動量密度でもあるから、レバー内部に下向きの運動量が存在している…というのがラウエの鋭い着眼だ。
「下向きに動いている物がないのに、なぜ下向きの運動量などが存在するのだ?」という点を疑問に思う方もいるだろう。この追加のエネルギー・運動量は、上でも触れたように、内部応力を担う物質場に起因するものだったが、そういう場の代表例の電磁場では「何も動いていなくても運動量を持つ」ことがあることを思い出そう。例えば静電場 \(\V{E}\) と静磁場 \(\V{B}\) だけが存在する場合、(至るところそれらが平行という特殊な場合を除き)Poynting vector \(\V{E} \times \V{B}\) が存在するので、この空間には運動量が満ちている、ということになる。「動いている物」などまったく存在しないにもかかわらず。直角レバーの場合も話は同様で、レバーの内部応力を担う物質場は、別に何かが下向きに動いているわけではなくとも下向きの運動量を持つことが可能、というわけだ。
これらラウエの考察については、
http://www7b.biglobe.ne.jp/~kcy05t/nirigha.html
の続きの部分で“”偽の”回転中心”“仮想の回転中心”“非実在的なエネルギーの流れ”“”仮想の”運動量”などと否定されているが、それが誤解であることを以下補足しておく。
角運動量の基準点(「回転中心」)について
上で注意した通り、もともと角運動量というものは「考えている慣性系での固定点」を基準点として定義されるものだ。したがって、上のページの“K 系(引用者注・上述の通り、本記事中では \(K’\) 系)の観測者の地点に偽の回転中心を設定した。この仮想中心はレバーとは何の繋がりもないためまったく無意味なのにである。”という非難はまったく当たらない。レバーが動いて見える慣性系 \(K’\) では、「観測者の地点」のような固定点こそがまず基準点にふさわしい点として真っ先に挙がる点なのだ。つまり、ラウエの議論が観測者の位置に基準点を取っているのは、角運動量というものを考える上で最も基本的な原則に沿っているに過ぎず、そのせいで何か不適切なことが起こったりするようなことはありえない。
もちろん、
\begin{equation}
\label{eq:relativity-paradox-8}
\text{レバーの支点から計った位置ベクトル} \times \text{運動量}
\end{equation}
という「角運動量に類似した量」を作って、その和に着目することは別に問題ないし、それが有用である場面も存在する。\(K’\) での支点の位置ベクトルを \(\V{z}\) として、\(K’\) で計算した\eqref{eq:relativity-paradox-8}の和を \(\V{J}\) と書くと
\begin{align}
\V{J} &= \sum_{i} (\V{r}_{i} – \V{z}) \times \V{p}_{i} = \sum_{i}
(\V{r}_{i} \times \V{p}_{i} – \V{z} \times \V{p}_{i} ) \notag\\
&= \sum_{i} \V{r}_{i} \times \V{p}_{i} – \V{z} \times \sum_{i} \V{p}_{i}
\notag\\
\label{eq:relativity-paradox-13}
&= \V{L} – \V{z} \times \V{P}
\end{align}
となる(ただし、\(\V{P} = \sum_{i} \V{p}_{i}\) は全運動量)。これは\eqref{eq:relativity-paradox-6}と似た形の式だが、\eqref{eq:relativity-paradox-6}の \(\V{b}\) と違って \(\V{z}\) は一定ではない。しかし、\(K’\) の原点をレバーの支点の軌跡の直線上に取れば \(\V{z} \parallel \V{P}\) となるので、\eqref{eq:relativity-paradox-13}より \(\V{J} = \V{L}\) となって、結果として類似量 \(\V{J}\) でも \(\V{L}\) と同じベクトルが得られる。今の場合、\(K’\) でのレバーは各素片がすべて同じ速度 \(\V{u}\) で動き、そのため\eqref{eq:relativity-paradox-8}が時間によらない一定のベクトルになるが、そういう場合に今の計算法を使うと角運動量 \(\V{L} = \V{J}\) を最初から時間によらない定ベクトルの形で見通しよく計算できるわけだ。
しかし、だからと言って「支点を回転の中心に取るのが正しく、観測者の地点は“”偽の”回転中心”“仮想の回転中心”だ」などと考えるのはまったくの的外れである。話はあべこべで、「慣性系での固定点を基準点として初めて角運動量 \(\V{L}\) が確固たる量として定義でき、\(\V{L}\) との比較によって『角運動量の類似量』\(\V{J}\) でも行けることが『結果的に』わかる」だけだ。概念上は、\(\V{J}\) は \(\V{L}\) の後に立つ量であって、\(\V{J}\) が \(\V{L}\) に先行したりするわけではない。
なお、今の例で「角運動量の類似量」である\eqref{eq:relativity-paradox-8}の和\(\V{J}\) が角運動量 \(\V{L}\) に一致したのは、以下のようなかなり特殊な条件に強く依存している。
- レバーのどの点も同じ速度 \(\V{u}\) で動いている
- 原点を\eqref{eq:relativity-paradox-8}の変位ベクトルの基準点の軌跡上に取った
なので、一般には \(\V{J} = \V{L}\) と決めてかかってはいけない。
外力がレバーになす仕事とエネルギー流束の実在性について
上のページでは、“レバー内の仮想のエネルギー流は幻想である。”と題して、ラウエが気づいたエネルギー流束・運動量密度を“理不尽な前提条件に依存”する“非実在的なエネルギーの流れ”“”仮想の”運動量”と退けているが、その議論は正しくない。順に見ていこう。
“まず最初に、レバーのトルクがゼロ(もしくは弱まっている)とき、力 Fx は地点”1″に対して仕事をしない。”と主張されているが、そんなことはない。仕事の定義は力と微小変位の内積であり、\(K’\) 系では地点”1″が右向きの速度を持つ以上、力 \(F_{\text{x}}\) は「イヤでも」仕事をする(してしまう)のである。
これは、上で導出した通り運動方程式からほんのわずかの式変形で得られる確固とした関係であり、「力がはたらいている物体が力の方向に動いたら、その力から仕事を受ける」ことは避けようがない絶対の帰結だ。
したがって、上のページで“仕事をしない”ことの理由として述べられている“(レバーは剛体のため、この力 Fx は Fy によって遠隔的にキャンセルされるからである。)”という主張は誤りだ。そんな魔法のような不思議な効果が発生したりはしない。\(F_{\text{y}}\) は運動の方向と垂直なので仕事をしないが、レバーは \(F_{\text{x}}\) の方向には動いているので、力 \(F_{\text{x}}\) からは間違いなく仕事を受ける。受けざるを得ず、それを避けることはできない。この文は、続く文章が以下のようになっている所から推測すると、「慣性系 \(K\) ではレバーが止まっているのでどの力からも仕事を受けない」ということ(これは正しい)と、「レバーが動く慣性系 \(K’\) で仕事を受けない」ということ(こっちは誤り)の一時的な混同が起きているのではないだろうか。
“例えば、力 (= F ) が釣り合った静止した直角レバーがあるとする。このときこの力 F は レバーが静止しているため仕事をしていない。
しかし上記の不合理な定義が正しいとすると、観測者が左方向へ動き始めるとレバーは右方向へ動いて見えるため、この力が仕事をし始めることになる。もちろんこんなことはあり得ない。”
ここで“あり得ない”と断言されているのは、
ある特定の力に着目したとき、その力に仕事を受けるか、受けないか、というのは、慣性系の取り方によらず客観的に決まる
と思っているからであるように見えるが、だとしたらその考えは正しくない。微小仕事の式 \(\V{F} \cdot \V{v} \Delta t\) で、\(\V{v}\) は慣性系によって変わるから、\(\V{v} = \V{0}\) に見える慣性系では仕事は \(0\) で、そうでない慣性系では \(0\) でない仕事を受ける、なんてことはごく当たり前に起きる。これは相対論を持ち出すまでもなく、Newton 力学の段階でただちに言えることだ。上で説明した、床の上で荷物を引っ張る話でも、引っ張る力に荷物が仕事を受けるかどうか、というのは、慣性系の取り方によって簡単に変わってしまっていた。
つまり、上で“あり得ない”とされている“観測者が左方向へ動き始めるとレバーは右方向へ動いて見えるため、この力が仕事をし始めることになる”なんてことは、たやすく発生するありきたりの出来事に過ぎない(摩擦あり荷物の場合、摩擦力も合わせた合力から受ける「正味の仕事」はどちらの慣性系でも \(0\) になるが、そのことと混同してはいけない。直角レバーの話で着目されていたのは「\(F_{\text{x}}\) という単一の力から」仕事を受けるかどうか、であって、「レバー全体が受ける合力」は議論していなかったわけだから、それに対応するのはこの場合でも合力ではなく「引っ張る力」という単一の力である)。
“この奇妙なエネルギーが速度 U でレバー内をA地点のほうへ流れていくと強引に仮定した。”や“非実在的なエネルギーの流れ”といった表現からは、ラウエの議論に現れる「レバー内のエネルギー流束」は虚構であり実在しない、という認識が読み取れる。しかし、Newton 力学の段階でエネルギー流束の存在が理解できることは上で示した通りで、このエネルギー流束は紛れもない実在のものである。
さて、こうやって「直角レバーのパラドックス」に触発されて、エネルギー・運動量や力・仕事、角運動量・トルクについていろいろ考えたり調べたりしているうちに、これまで表面的にしか理解していなかったエネルギー運動量テンソルについての理解がちょっと深まったのだが、その過程で「エネルギー運動量テンソル(あるいは、応力テンソル)が対称テンソルになる理由のよくある説明って、実は理由になっていないんじゃ………?」ということに気づいた。詳しくはまた次回に。
コメントを残す