\(\DeclareMathOperator{\Gal}{Gal}
\newcommand{\rnsg}{\mathrel{\vartriangleright}}
\newcommand{\field}[1]{\mathbb{#1}}
\newcommand{\Q}{\field{Q}}
\newcommand{\zettaiti}[1]{\lvert #1 \rvert}
\)
以下の文章で、「本文書」というのは「ガロア理論入門ノート」のことを指す。
この記事も、前回同様、\(K \to L\) のような矢印で体の拡大を表すことにする。
定理37の後半に踏み込む前に、以前言及した通り、定理37の中で命題15を利用する準備をしておこう。まず「組成列」に触れておく。
■ 本文書 p.14 定義(2) の組成列の定義は、文章が「さらに」で始まっているので結構紛らわしい。私は最初、「直前の文章の可解群の定義に現れる条件(\(G_{i-1}/G_{i}\) がすべて可換群)をみたしており、それに加えて \(G_{i-1}/G_{i}\) がすべて単純群になっているという条件もみたしているような列」を組成列と言うのかとばかり思い込んでしまったが、他の文献も参照してみるとどうもそういうことではないらしい。実際には直前の文章とは独立していて、「\(G_{i-1}/G_{i}\) が単純群かどうかだけが『組成列』の定義に関与していて、可換かどうかは問わない」ということのようである。したがって、2つの文章をつなぐ接続詞としては、「さらに」ではなく例えば「また」などの方が紛れがなくてよかったのではないかと思う。
■ 命題15を利用する上でポイントとなるのは、以下の補題である。「\(H\) は群 \(G\) の極大な正規真部分群とする。すなわち、\(H\) を真に含むような正規部分群は \(G\) しかないとする。このとき、\(G/H\) は単純群である」
【補題の証明】 正規部分群 \(H\) による割り算による自然な準同型写像を \(\varphi\) とする。もし \(G/H\) が自明でない正規部分群 \(N\) を持つと、\(\varphi\) による引き戻しで \(G\) と \(H\) の間に正規部分群 \(\varphi^{-1}(N)\) が存在することになり、\(H\) の極大性に反する(準同型写像による正規部分群の引き戻しはやはり正規部分群になることに注意)。
\[
\begin{array}[b]{ccccc}
G & \rnsg & \varphi^{-1}(N) & \rnsg & H \\
\downarrow{\scriptstyle \varphi} & & \downarrow{\scriptstyle \varphi} & &
\downarrow{\scriptstyle \varphi} \\
G/H & \rnsg & N & \rnsg & \{e’\} = \{H\}
\end{array}
\]
よって \(G/H\) は自明な正規部分群しか持たないから、単純群か単位群である。\(G/H\) が単位群になるのは \(G=H\) のときだけだから、\(H\) が真部分群という仮定により、\(G/H\) は単純群である。\(\square\)
■ 以上の準備によって、定理37の中での命題15の使いどころが説明できるようになった。「有限可解群は、正規列の商群がすべて素数位数の巡回群になるように正規列を取れる」ということを示すのに命題15を使う。
【証明】
有限可解群 \(G=G_{0}\) に対して、その極大な正規真部分群を \(G_{1}\) とする(有限性によって、\(G\) が単位群でなければ \(G_{1}\) は必ず取れる。\(G\) が単位群の場合は元々正規列 \(G_{0}=\{e\}\) が長さ \(1\) なので、商群が発生しないため、示すべきことがない)。上の補題によって \(G_{0}/G_{1}\) は単純群だが、可解群でもある(\(G_{0}\) が可解群なので)から、命題15により素数位数の巡回群である。
次に、\(G_{1}\)(これも有限可解群)が単位群でなければ、その極大な正規真部分群 \(G_{2}\) を取ると同様のことが起きる。以下これを繰り返していくと、位数
\[ \zettaiti{G_{0}} > \zettaiti{G_{1}} > \zettaiti{G_{2}} > \dots \]
は狭義単調減少だから無限に続くことはない。どこかで \(G_{r}\) が単位群になって終わる。
このとき、正規列
\[ G=G_{0} \rnsg G_{1} \rnsg \dots \rnsg G_{r} = \{e\} \]
は組成列であり、商群 \(G_{i-1}/G_{i}\) はすべて素数位数の巡回群である。\(\square\)
■ なお、今の証明では \(G\) の可解性を仮定していたが、\(G\) の有限性だけを仮定して同様の議論を行うことで、「どんな有限群も組成列を持つ」ことが確かめられる。定理37後半の証明中で、さらっと「組成列を考える」と言っているのはそういう事情なのだろう。
■ 定理37後半を読み解く前に、2点コメントしておく。まず、ここで示そうとしていることは、大抵「方程式のガロア群が可解群ならばべき根で解ける」のように言い表されるが、以前触れたことに沿って述べると、実際に示しているのは「解ける」ではなく「解が存在する」であることに注意しよう。直接証明されているのは、「べき根拡大を有限回行った体の『どこかには』解が存在している」ということであって、それ自身は直接「解をべき根で表す表式」を与えているわけではない。ではどうすれば「具体的な解の表式」が得られるのか、ということは後日別記事にて。
また、以前触れた通り、この定理37後半では、本文書の元々の「(広義)べき根拡大」の定義通り、添加するべき根 \(\sqrt[n]{a}\) としては最小多項式が \(X^{n}-a\) になっているもののみに限定する。
■ 定理37後半の証明に移る。本文書で約数関係でちょっと記述が不足しているところを補い、また、ちょっと記号の使い方を変えておく。
\(n=\zettaiti{\Gal(L/K)}\) に関する数学的帰納法を用いる。\(n=1\) の場合は \(L=K\) だからすべての解が \(K\) の中にあるので OK。
\(n\) 未満の拡大次数の可解なガロア拡大は、すべてべき根で構成できるとする。\(1\) の原始 \(n\) 乗根を \(\zeta\) とすると、定理34により \(K(\zeta)\) は \(K\) のアーベル拡大。さらに、\(\zettaiti{\Gal(K(\zeta)/K)} = [K(\zeta):K] < n\) なので、数学的帰納法の仮定により \(X^{n}-1=0\) はべき根で解ける。つまり、\(K\) の広義べき根拡大 \(M\) で、\(K(\zeta) \subset M\) であるものが存在する。
\(f(X)\) の \(M\) 上の最小分解体を \(\tilde{L}\) とする。当然、\(\tilde{L} \supset L\) である。
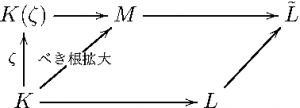
この図から、目標を達するには、\(\tilde{L}\) が \(M\) の広義べき根拡大であることを示せばよい(2段階の広義べき根拡大の積み重ねは、やはり広義べき根拡大になるから)。
補題35より、\(\Gal(\tilde{L}/M)\) は \(\underbrace{\Gal(L/K)}_{\text{可解群}}\) の部分群と同型だから、次の2つがなりたつ。
(1) \(\Gal(\tilde{L}/M)\) も可解群。
(2) \(\zettaiti{\Gal(\tilde{L}/M)} \leqq \zettaiti{\Gal(L/K)}=n\)
ここで、もし(2)で等号が成立していなければ、(1)および数学的帰納法の仮定から、\(\tilde{L}\) が \(M\) 上べき根で構成されるので示された。よって以下では(2)で等号が成立する場合を考える。
(1)より、上の予備考察から、\(M\) から(素数次数の)巡回拡大だけを積み重ねて \(\tilde{L}\) に達することができる。
\begin{gather}
\label{eq:19-1}
M=M_{0} \to M_{1} \to \dots \to M_{r} = \tilde{L} \\
\text{$M_{i}$ は $M_{i-1}$ の(素数次)巡回拡大} \notag
\end{gather}
ここで、
\[ [\tilde{L}:M] = [M_{r}:M_{r-1}] \dotsm [M_{1}:M_{0}] \]
より、拡大次数 \(p_{i} = [M_{i}:M_{i-1}]\) はすべて \([\tilde{L}:M] = \zettaiti{\Gal(\tilde{L}/M)} = n\) の約数である。そして \(M\) が \(1\) の原始 \(n\) 乗根 \(\zeta\) を含んでいるので、\(M_{i-1}\) は \(1\) の原始 \(p_{i}\) 乗根を含む。したがって定理33より \(M_{i}\) は \(M_{i-1}\) の単純べき根拡大と言え、\eqref{eq:19-1}は広義べき根拡大。\(\square\)
■ 途中の等号成立・不成立についての場合分けは、「部分群の要素数は、親の群の要素数の約数」という事実を使えばいらない(\([\tilde{L}:M]\) が \(n\) ではなく「\(n\) の約数」に変わるだけだから)が、本文書ではそれは証明されてなかったので、一応回避してみた。もちろん、証明したければ容易なことではある。
■ ミスプリとしては、途中で \(\tilde{L}\) や \(\tilde{M}\) の上のチルダ記号がずれてしまっている箇所がある。
コメントを残す