ガロア理論入門ノートについて・その11

\(\DeclareMathOperator{\Gal}{Gal}
\DeclareMathOperator{\Img}{Im}
\newcommand{\lnsg}{\mathrel{\vartriangleleft}}
\newcommand{\field}[1]{\mathbb{#1}}
\newcommand{\Q}{\field{Q}}
\newcommand{\zettaiti}[1]{\lvert #1 \rvert}
\)
以下の文章で、「本文書」というのは「ガロア理論入門ノート」のことを指す。

最初に、この記事での記法の約束を述べる。「\(K \to L\)」のように書いた場合、矢印は体の拡大を表すものとする。さらに、この記事だけで通じる記法として、矢印には、「\(\Q \xrightarrow{\sqrt{2}} \Q(\sqrt{2})\)」のように添加するべき数を添えて書くこともある。また、「\(K \xrightarrow{\text{べき根拡大}} L\)」と書いたら広義べき根拡大を表しているものとする。

なお「ガロア拡大」という用語の用法は本文書に従っているので、標数が \(0\) でない体を扱っている場合は以下の文章には正しくない部分が現れるものと思われるので注意されたい。

■ 前回、最高次の係数が \(1\) でない場合に（方程式の可解論の本質とは関係ないような）煩雑さが生じることを見たので、定理37も方程式の両辺を最高次の係数で割った上で考えるべきものであることに注意しておく。実際、本文書の証明も最高次の係数を \(1\) にした上で議論されている。また、前回「方程式（多項式）のガロア群」と言った場合は、本来ベースとなる体を指定しないと定義されないはず、と指摘したが、それに沿って考えた場合、定理37の同値記号の右側の「\(f(X)\) のガロア群」にもベースとなる体を指定する必要が出てくる。これは、証明本体にも表れているが、「最高次の係数を \(1\) にした後の \(f(X)\) の係数をすべて \(\Q\) に添加した体」がそれである。
■ 定理37の証明では、最初のうちは文字 \(n\) は方程式の次数を表していたのに、前半の「\(\implies\)」の証明ではべき根の指数になり、後半の「\(\impliedby\)」の証明ではガロア群の位数（要素数）になっていて、重複して使われている。
ここは、形式的にはまずいと言えばまずい。しかし、いずれの場合も用法の違いは文脈から明らかで、重複によって議論が混乱したり誤りにつながるような際どい交錯が起きたりもしていないので、別に気にする必要はないだろう。
■ 定理37を読み解く準備として、定理37は全面的に次の構図を利用しているという点に注意しておく。

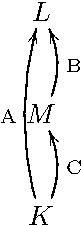
体の拡大列 \(K \to M \to L\) に対して、拡大 \(K \to L\), \(M \to L\), \(K \to M\) に図のように A, B, C と名前をつけておくと、
\[ \text{Aが有限次ガロア拡大} \implies \text{Bが有限次ガロア拡大}
\text{（系27）} \]
Aが有限次ガロア拡大のとき、
\[ \text{Cがガロア拡大} \iff \Gal(L/M) \lnsg \Gal(L/K) \]
で、そのもとで
\[ \Gal(L/K) / \Gal(L/M) \cong \Gal(M/K) \]
だった（系31）。これらと以前注意したことを合わせると、A, Cが有限次ガロア拡大のとき
\[ \text{Aが可解拡大} \iff \text{B,Cが可解拡大} \]
という関係が得られる。この「\(\impliedby\)」の方は、大まかには「可解拡大を有限回積み重ねた結果がガロア拡大になっていれば、それはやはり可解拡大」ということを意味している。また、逆の「\(\implies\)」の方の意味は「可解拡大を有限回のガロア拡大に分割した場合、その１つ１つのガロア拡大もやはり可解拡大」ということになる。

これらの「有限回」は何回でもよい。上で述べた２回の場合を繰り返し適用すれば示せる。例えば、\(K_{0} \to K_{1} \to K_{2} \to K_{3}\) という拡大列で、３つのステップ \(K_{i-1} \to K_{i} \; (i=1,2,3)\) がすべて可解拡大（従ってガロア拡大）で、しかも全体としての拡大 \(K_{0} \to K_{3}\) が有限次ガロア拡大だったとしよう。この場合、\(K_{0} \to K_{3}\) が可解拡大でもあることを示したければ、上の「\(\impliedby\)」を適用すると、\(K_{1} \to K_{3}\) が可解拡大であることを示せばよいことになる。今 \(K_{0} \to K_{3}\) が有限次ガロア拡大だから \(K_{1} \to K_{3}\) も有限次ガロア拡大なので、１ステップ少ない場合に帰着された。これを繰り返せばよい。
■ 前項で述べたことにより、ある有限次ガロア拡大 \(K \to L\) が可解拡大であることを示したい場合に、「直接示す」以外に次の２通りの作戦がありうることが見て取れる。
[1] 拡大をうまく分割してやると、各ステップが可解拡大になるように取れることを示す
[2] \(L\) を拡大した体 \(\tilde{L}\) をうまく作ると、\(K \to \tilde{L}\) が可解拡大になるように取れることを示す
■ まずは定理37の前半、「べき根で解ける方程式のガロア群は可解群である」の証明を詳しく見て行こう。

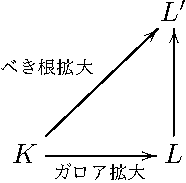
方程式を最高次の係数で割った上で、\(K\) を方程式の係数体、\(L\) を最小分解体とし、\(K\) の広義べき根拡大 \(L’\) が \(L\) を含むように取れたとすると上図のような構図である。ただしここでは、以前触れたように広義べき根拡大の定義を修正し、添加するべき根の最小多項式が \(X^{n}-a\) の形であることは要求しないでまずは考える（定理37の後半によって、\(1\) の原始 \(n\) 乗根がすべて \(X^{n}-a\) の形の最小多項式を持つべき根添加のみで作れることが判明した後で改めてここに戻ってきた暁には、本文書の広義べき根拡大の元々の定義通り、添加するどのべき根も \(X^{n}-a\) の形の最小多項式を持つと仮定して構わなくなる）。

目標は \(K \to L\) が可解拡大であることの証明で、これは[2]を踏まえると「\(K \to L’\) が可解拡大」を示せばいいと思いたくなる。しかし、それは早合点で、一般に広義べき根拡大 \(K \to L’\) はガロア拡大になっているとは限らないので、それではうまく行かない（例えば
\[ \Q \xrightarrow{\sqrt[3]{2}} \Q(\sqrt[3]{2}) \xrightarrow{\sqrt{2}}
\Q(\sqrt[3]{2}, \sqrt{2}) \]
も広義べき根拡大だが、これは \(\omega\) を含んでいないからガロア拡大になっていない）。

そこで一工夫したのが \(L”\) の導入である。

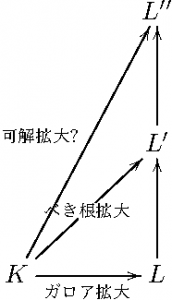
目標を、次を示すことに定める。

\(K \to L’\) が広義べき根拡大であるとき、\(L’\) の拡大体 \(L”\) を、\(K \to L”\) が（有限次ガロア拡大で、かつ）可解拡大であるように取れる………☆

これが言えれば[2]から \(K \to L\) が可解拡大であることが言えるので、「べき根で解ける方程式のガロア群は可解である」が示せたことになる。なお、☆の形にしてしまえばもう \(L\) が出てくる余地はないので、以下の話でも \(L\) はもう表に現れない。主役は \(K\), \(L’\), \(L”\) である。

定理37の前半で、\(r\) についての数学的帰納法で証明しようとしているのはこの☆である。

(i) \(r=1\) の場合
体の関係図を少し斜めにして書いたものが次の図である。\(r=1\) なので、広義べき根拡大 \(K \to L’\) は \(a \in K\) の \(n\) 乗根（のひとつ）\(\sqrt[n]{a}\) の添加１回で実現されている。

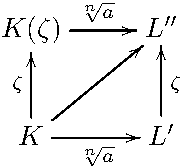
\(K\) に \(1\) の原始 \(n\) 乗根 \(\zeta\) を添加した体が \(K(\zeta)\) で、それにさらに \(\sqrt[n]{a}\) を添加した体を \(L”\) とすると \(L”=L'(\zeta)\) でもあるから、図のようになっている。\(K \to L”\) が（有限次ガロア拡大で、かつ）可解拡大であることを示せば、\(r=1\) の場合の☆の証明は完了。

まず、\(L”\) は \(K\) 上の \(X^{n}-a\) の最小分解体なので、\(K \to L”\) は有限次ガロア拡大である。なので、可解拡大でもあることを示すには、今度は[1]を参照して、次の２つを示せばよい。
1. \(K \to K(\zeta)\) は可解拡大。
2. \(K(\zeta) \to L”\) は可解拡大。
そして、1.は定理34より成立し、2.は定理33(2)より成立する。よって \(r=1\) の場合は☆は成立。

(ii) \(r \geqq 2\) で、\(r-1\) までは☆が成立しているとする。広義べき根拡大 \(K \to L’\) の最後のステップを \(K’ \xrightarrow{\sqrt[n]{a}} L’\) とする。

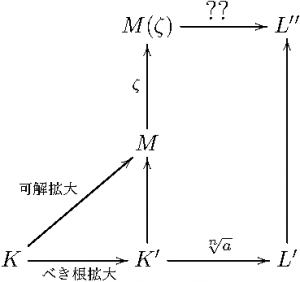
\(K \to K’\) は \(r-1\) 段の広義べき根拡大だから、数学的帰納法の仮定から \(K’\) の拡大体 \(M\) を、\(K \to M\) が（有限次ガロア拡大で、かつ）可解拡大であるように取れる。\(1\) の原始 \(n\) 乗根を \(\zeta\) とし、\(M(\zeta)\) の拡大体 \(L”\) をうまく作って、\(r\) の場合の☆を示すことを考えよう。そのためには、図の「??」で添加する数を上手に選んで、\(L”\) が \(L’\) の拡大体になり、かつ \(K \to L”\) が可解拡大になるようにすればいい。

\(r=1\) の場合を思い出すと、「??」では \(\sqrt[n]{a}\) を添加すればいいようにも思える。しかしその場合、\(L”\) が \(L’\) の拡大体になることは確かだが、\(K \to L”\) がガロア拡大になるとは限らなくなる。\(a\) は \(K’\) の元ではあっても \(K\) の元とは限らないので、「??」で \(\sqrt[n]{a}\) を添加するだけでは \(K\) 上の共役性に対する対称性が保証されないからだ。

対称性を回復するために、「??」では共役な元をすべて添加しよう。\(K\) 上で \(a\) と共役な数の全体を \(a_{1}=a, a_{2}, \dots, a_{m}\) とする。\(M\) は \(K\) のガロア拡大で \(a \in M\) だから、このような共役元の存在は保証され、それらはすべて \(M\) の元である。そして、「??」では \(\sqrt[n]{a_{1}}, \dots, \sqrt[n]{a_{m}}\) をすべて添加したとしよう（\(\zeta\) を含む体 \(M(\zeta)\) に添加するので、\(i>1\) に対して \(\sqrt[n]{a_{i}}\) が \(n\) 個ある \(n\) 乗根のうちどれを指すのかを気にする必要はない。どれを添加しても \(n\) 個全部添加するのと同じことになる）。この場合、\(L”\) が \(L’\) の拡大体になるのは当然だが、さらに以下のようにして \(K \to L”\) が可解拡大であることも言える。

先ほどの[1]を参照すると、次の４つを示せばよいことになる。
1. \(K \to L”\) は有限次ガロア拡大。
2. \(K \to M\) は可解拡大（仮定により成立）。
3. \(M \to M(\zeta)\) は可解拡大（定理34より成立）。
4. \(M(\zeta) \to L”\) （あるいは、それを更に細かく分割した各ステップ）は可解拡大。

まず、1. を示そう。\(M\) が \(K\) の有限次ガロア拡大であることから、\(M\) はある \(K\) 係数多項式 \(F(X)\) の \(K\) 上の最小分解体になっている。一方、\(L”\) は \(M\) に \(g(X)=(X^{n}-a_{1})(X^{n}-a_{2}) \dotsm (X^{n}-a_{m})\) の根をすべて添加した体である。\(g(X)\) は \(a_{1}, \dots, a_{m}\) について対称なので、展開すれば \(K\) 係数の多項式である（\(a_{1}, \dots, a_{m}\) は \(K\) 上で共役な数の全体だったので）。

以上から \(L”\) は \(F(X)g(X)\) の \(K\) 上の最小分解体だから、1. はなりたつ。

次に 4. を示す。\(M(\zeta) \to L”\) は \(\sqrt[n]{a_{i}} \; (i=1, \dots, m)\) を順に添加するステップに分解できるが、その各ステップは定理33(2)より可解拡大である。よって 4. もなりたつ。

以上で、\(r-1\) の場合を仮定して \(r\) の場合も言えた。

(i)(ii) より、数学的帰納法によって☆が証明された。\(\square\)

■ この証明からわかるように、以前触れた通り、定理36は特に必要としない。本文書では「\(M(\zeta) \to L”\) がアーベル拡大になる」ことを示すために定理36を使っているが、アーベル拡大という強いことまで言わなくとも、ここで目標のために必要となるのは可解拡大ということだけなので、上の説明のようにすれば十分になっている。
■ さらに、本文書では \(K \to M(\zeta)\) が可解拡大になることも示しているが、それも実は必要ではない。目標が「\(K \to L”\)」の可解性なので、上のように 1. 2. 3. 4. のステップに分割してしまえば済んでしまうわけである。
■ 本文書の \(r=1\) の場合の証明の終わり近くの「\(\Gal(K(\zeta)/K)\), \(\Gal(L”/K(\zeta))\) はともにアーベル拡大である」は「…アーベル群である」のミスプリ。
■ なお、☆の証明には実は数学的帰納法は不要だった。上の「??部で共役な \(n\) 乗根すべてを添加する」という手続きを、すべてのべき根添加に対して実行すればいいだけだった。詳しく述べるとこうなる。

広義べき根拡大
\[ K=K_{0} \subset K_{1} \subset \dots \subset K_{r} \]
があるとする（個々の拡大 \(K_{i} \to K_{i+1}\) は単純べき根拡大）。ここで、途中の \(\sqrt[n]{a}\) を添加するステップをすべて次の２段階のステップで置き換えてみる。

○ \(1\) の原始 \(n\) 乗根を添加する
○ \(a\) と \(K\) 上共役なすべての数 \(a, a’, a”, \dotsc\) に対して、\(\sqrt[n]{a}, \sqrt[n]{a’}, \sqrt[n]{a”}, \dotsc\) を添加する

このようにして作られる体を \(M_{0}=K, M_{1}, M_{2}, \dotsc\) とすると各 \(i\) に対して \(K_{i} \subset M_{2i}\) となるから、特に \(K_{r} \subset M_{2r}\) である。

さらに、作り方から各 \(M_{i}\) はすべて \(K\) の有限次ガロア拡大である。また、各 \(i\) に対して \(M_{i+1}\) は \(M_{i}\) のアーベル拡大である。よって特に、\(M_{2r}\) は \(K\) の有限次ガロア拡大で、かつ可解拡大でもある。

以上から☆は示された。\(\square\)