\(\newcommand{\field}[1]{\mathbb{#1}}\newcommand{\Q}{\field{Q}}\newcommand{\C}{\field{C}}\newcommand{\Gal}[1]{\operatorname{Gal}(#1)}\renewcommand{\dotsc}{\cdots}\newcommand{\zettaiti}[1]{\lvert #1 \rvert}\)以前の、可約な方程式の解を実際にべき根で求める手順で、ガロア理論の「中間体と部分群の1体1対応」を利用する所にはまだ遠回りしている箇所があった。そこでは、群の第二準同型定理なんていうものを利用していたが、ここはもっとはるかに簡単にカタがつくことだった。ガロア理論をちゃんと血肉としている人から見れば当たり前のことなのに、それにまったく気づいていないというお恥ずかしい話だった。
この記事も、ぎりぎり2020年中に書き終わってはいたのだが、こうやって公開するのは結構遅くなってしまった。
使うのは、これまでもしばしば登場してきた、ガロア理論の次の定理だ。
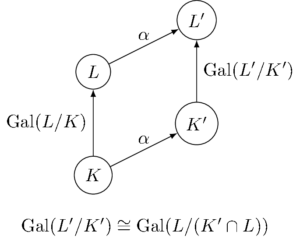
体 \(L\) は体 \(K\) のガロア拡大体とする。 \(K\), \(L\) にそれぞれ \(\alpha\) を添加した体を \(K’=K(\alpha)\), \(L’=L(\alpha)\) とすると、\(L’\) も \(K’\) のガロア拡大体であり、新しいガロア群 \(\Gal{L’/K’}\) は元のガロア群 \(\Gal{L/K}\) の部分群と同型。(より詳しくは、\(K’\) の「元の拡大体 \(L\) の中での正味の拡大」\(K’ \cap L\) を \(K”\) とするとき、
\[ \Gal{L’/K’} \cong \Gal{L/K”} \]
である)
さて、可解な方程式を解く話に戻ろう。\(\Q\) 係数方程式 \(f(x)=0\) のガロア群 \(G_{0}\) が可解で、組成列
\begin{equation}
\label{eq:howto-new6-4}
G_{0} \rhd G_{1} \rhd \dots \rhd \{1\}
\end{equation}
がわかっているとしよう。組成列は、隣り合う群どうしの要素数比 \(\zettaiti{G_{i}}/\zettaiti{G_{i+1}}\) が素数になるよう取ってあるとする。
組成列のうち、着目している隣り合う群が \(G\), \(H\) だとし、対応する体を \(K\), \(L\) とする。前回の記事で \(K’\) と書いていたものを、ここでは(上の定理に合わせるために)\(L\) と書いているので注意。
\(\zettaiti{G/H} = \zettaiti{G}/\zettaiti{H} = p\) は素数となり、\(\Gal{L/K}\) は \(p\) 次巡回群である。\(L\) は、\(K\) の何らかの数 \(A\) の \(p\) 乗根 \(\sqrt[p]{A}\) を \(K\) に添加した体になっている: \(L=K(\sqrt[p]{A})\)。\(A\) は未知であることに注意しよう(\(p\) は当然ながら既知)。なお、\(K\) が \(1\) の原始 \(p\) 乗根を含んでいない場合は \(\sqrt[p]{A}\) の形の数の添加ではうまく行かないこともあるが、いずれにせよ \(K\) に何らかの複素数を添加すると \(p\) 次巡回拡大体 \(L\) ができることは変わらないので、この添加する複素数を以下 \(\sqrt[p]{A}\) と略記してしまう。
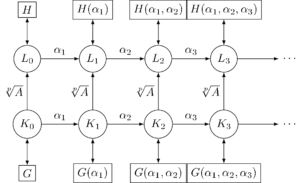
元の \(\Q\) 係数方程式 \(f(x)=0\) の解を \(\alpha_{1}, \alpha_{2}, \dots, \alpha_{n}\) とする。図のように、\(K_{0}=K\) に \(\alpha_{1}, \alpha_{2}, \dotsc\) を順に添加した体を \(K_{1}, K_{2}, \dotsc\) とし、\(L_{0}=L\) に \(\alpha_{1}, \alpha_{2}, \dotsc\) を順に添加した体を \(L_{1}, L_{2}, \dotsc\) とする。これも、前回の記事では \(K\), \(M\), \(L\) と書いていたものがここでは \(K_{0}\), \(K_{1}\), \(K_{2}\) になり、\(K’\), \(M’\), \(L’\) と書いていたものをここでは \(L_{0}\), \(L_{1}\), \(L_{2}\) と書いているので注意してほしい。また、添字 \(i\) と \(j\) の役割も混同しないでほしい。\(i\) は\eqref{eq:howto-new6-4}の組成列の群 \(G_{i}\) に対する添字で、この \(i\) を固定した上で \(G=G_{i-1}\) と \(H=G_{i}\) に対応する体 \(K\), \(L\) に解 \(\alpha_{1}, \alpha_{2}, \dotsc\) を順次添加していくときの体 \(K_{j}\), \(L_{j}\) の添字が \(j\) である。
\(j=0,1, \dotsc\) のすべてに対し、\(L_{j} = K_{j}(\sqrt[p]{A})\) となっている。
ふたつの体の列 \(K_{0}, K_{1}, \dotsc\) と \(L_{0}, L_{1}, \dotsc\) はどちらもいずれは \(f(x)\) の \(\Q\) 上の最小分解体となり一致する。\(K_{n}=L_{n}\) および \(K_{n-1}=L_{n-1}\) は明らか(どちらも最小分解体)だが、場合によっては \(j<n-1\) で \(K_{j}=L_{j}\) となることもある。その場合、\(K_{j}=L_{j}\) となったからと言ってそれらが \(f(x)\) の最小分解体になるとは限らないが、一度 \(K_{j}=L_{j}\) となればその後の \(j\) でもずっと \(K_{j}=L_{j}\) となり続けることは明らかだ。
ここで、上の定理を繰り返し適用すると、\(\Gal{L_{1}/K_{1}}\) は \(\Gal{L_{0}/K_{0}}\) の部分群(と同型)、\(\Gal{L_{2}/K_{2}}\) は \(\Gal{L_{1}/K_{1}}\) の部分群(と同型)…の繰り返しとなる。\(A\) が \(B\) の部分群と同型であることを
\[ B \succ A \]
で表すと
\begin{equation}
\label{eq:howto-new6-1}
\Gal{L_{0}/K_{0}} \succ \Gal{L_{1}/K_{1}} \succ \Gal{L_{2}/K_{2}} \succ
\dots
\end{equation}
である。
ところが、\eqref{eq:howto-new6-1}のはじめの \(\Gal{L_{0}/K_{0}}\) は \(p\) 次巡回群だから、その部分群は \(p\) 次巡回群か単位群のいずれかだ。そして、\eqref{eq:howto-new6-1}の最後の \(\Gal{L_{n}/K_{n}}\) は単位群である。よって、\eqref{eq:howto-new6-1}は途中まではずっと \(p\) 次巡回群で、ある所から先はすべて単位群となる。つまり、次のような番号 \(t\) が存在する。
\begin{equation}
\label{eq:howto-new6-2}
\underbrace{\Gal{L_{0}/K_{0}}, \dots, \Gal{L_{t-1}/K_{t-1}}}_{\text{$p$
次巡回群}}, \underbrace{\Gal{L_{t}/K_{t}}, \dots,
\Gal{L_{n}/K_{n}}}_{\text{単位群}}
\end{equation}
これに当たることを、前の記事ではわざわざ第二準同型定理なんてものを使って論じていたが、そんな必要は全然なかったのだ。置換群としての \(G\), \(H\) が具体的にわかっているという状況で、そのおかげで図の各体に対応する部分群 \(G(\alpha)\) 等もすべてわかっていたので、それに気を取られてそういった群を直接見ることしか考えていなかったが、ここでやったように、それらの比 \(G/H \cong \Gal{L_{0}/K_{0}}\), \(G(\alpha_{1})/H(\alpha_{1}) \cong \Gal{L_{1}/K_{1}}\) 等に着目した方がはるかに簡単に事情がわかったのだ。考えが浅かったというほかない。
話を続けよう。\eqref{eq:howto-new6-2}より
\[ L_{j} = K_{j} \quad (j=t, t+1, \dots, n) \]
で、これは次のことを意味する。\(j=0\) から \(j=t-1\) までは、\(K_{j}\) から上の体 \(L_{j}\) に「上がる」ためには \(\sqrt[p]{A}\) を添加しなければならないが、\(K_{t}\) になったとたんその \(\sqrt[p]{A}\) なしで \(K_{t}=L_{t}\) となった。これは、\(j=t\) にうつるときに添加した \(\alpha_{t}\) と \(K_{t-1}\) の数を合わせると \(\sqrt[p]{A}\) を作れるようになっているということで、言い換えると \(\sqrt[p]{A} \in K_{t-1}(\alpha_{t}) = K_{t}\) ということである。
また、\eqref{eq:howto-new6-2}から、\(j=t,t+1,\dots,n\) のとき
\begin{gather*}
G(\alpha_{1}, \dots, \alpha_{j}) = H(\alpha_{1}, \dots, \alpha_{j}) = H \cap G(\alpha_{1}, \dots, \alpha_{j}) \\
\therefore G(\alpha_{1}, \dots, \alpha_{j}) \subset H
\end{gather*}
であることもわかる。一方 \(j=0,\dots,t-1\) までは \(H(\alpha_{1}, \dots, \alpha_{j}) = H \cap G(\alpha_{1}, \dots, \alpha_{j})\) は \(G(\alpha_{1}, \dots, \alpha_{j})\) の真部分群だから
\[ G(\alpha_{1}, \dots, \alpha_{j}) \not\subset H \]
である。したがって、\(t\) は「初めて \(G(\alpha_{1}, \dots, \alpha_{j}) \subset H\) となる \(j\)」として特徴づけられる。
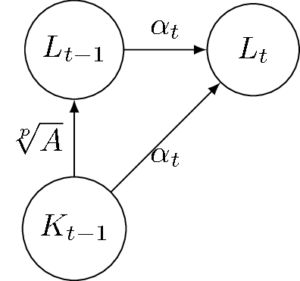
\(K_{t-1}\), \(L_{t-1}\), \(K_{t}=L_{t}\) の関係を図示すると、こうなっている。
この図と
\[ [L_{t}:K_{t-1}] = [L_{t}:L_{t-1}][L_{t-1}:K_{t-1}] \]
を見比べると、次のことがわかる。
- \(L_{t-1}\) は \(K_{t-1}\) の \(p\) 次巡回拡大だったから、\([L_{t-1}:K_{t-1}] = p\) である。
- よって、
\begin{equation}
\label{eq:howto-new6-3}
[L_{t}:L_{t-1}] = \frac{1}{p}[L_{t}:K_{t-1}]
\end{equation}
である。 - \([L_{t}:L_{t-1}]\) は、「\(L_{t-1}\) に \(\alpha_{t}\) を添加するときの拡大次数」で、\([L_{t}:K_{t-1}]\) は「\(K_{t-1}\) に \(\alpha_{t}\) を添加するときの拡大次数」だ。同じ \(\alpha_{t}\) を添加しているのに、\eqref{eq:howto-new6-3}は前者の拡大次数の方が後者の拡大次数の \(\frac{1}{p}\) 倍に縮小していることを意味する。つまり、\(\alpha_{t}\) の最小多項式は、\(L_{t-1}\) 成分のものと \(K_{t-1}\) 成分のものでは違っており、\(\sqrt[p]{A}\) の添加によって後者が因数分解されて、次数が \(\frac{1}{p}\) 倍になったものが前者になっている。
このようにして、最小多項式 \(g_{\alpha_{1}}(x), g_{\alpha_{2}}(x), \dotsc\) の中で、更新されるのは \(g_{\alpha_{t}}(x)\) であることがわかる。\(t\) を、いま既知である置換のリストから決定するには、次のようにすればいい。これは以前の記事と同じ手順ではあるが、上で得られた知見と見比べると理解が深まるだろう。
- \(G(\alpha_{1}), G(\alpha_{1},\alpha_{2}), \dotsc\) を求める。step2 以降なら、前 step での \(H(\alpha_{1}), H(\alpha_{1},\alpha_{2}), \dotsc\) がそっくりそのまま使えるので、改めて求める必要はない。
- \(H(\alpha_{1}) = H \cap G(\alpha_{1}), H(\alpha_{1},\alpha_{2}) = H\cap G(\alpha_{1},\alpha_{2}), \dotsc\) を求める。そして、\(H\) との共通部分を取っても変化がない最初の箇所を特定する。
- 変化があった最後は \(G(\alpha_{1},\dots, \alpha_{t-1})\) で、変化が起こらなかった最初は \(G(\alpha_{1},\dots, \alpha_{t})\) だ。これらに対応する体どうしの間に添加された解が \(\alpha_{t}\) で、その最小多項式が、この step で更新される最小多項式になる。
以下は、以前の記事と同様にすればよい。
井汲 景太 へ返信する コメントをキャンセル