新・方程式のガロア群の求め方 & ガロア群が可解である方程式の解き方その6

$\newcommand{\field}[1]{\mathbb{#1}}\newcommand{\Q}{\field{Q}}\newcommand{\C}{\field{C}}\newcommand{\Gal}[1]{\operatorname{Gal}(#1)}\renewcommand{\dotsc}{\cdots}\newcommand{\zettaiti}[1]{\lvert #1 \rvert}$以前の、可約な方程式の解を実際にべき根で求める手順で、ガロア理論の「中間体と部分群の１体１対応」を利用する所にはまだ遠回りしている箇所があった。そこでは、群の第二準同型定理なんていうものを利用していたが、ここはもっとはるかに簡単にカタがつくことだった。ガロア理論をちゃんと血肉としている人から見れば当たり前のことなのに、それにまったく気づいていないというお恥ずかしい話だった。

この記事も、ぎりぎり2020年中に書き終わってはいたのだが、こうやって公開するのは結構遅くなってしまった。

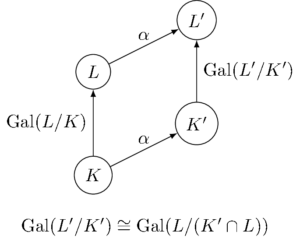
使うのは、これまでもしばしば登場してきた、ガロア理論の次の定理だ。

体 $L$ は体 $K$ のガロア拡大体とする。 $K$, $L$ にそれぞれ $\alpha$ を添加した体を $K’=K(\alpha)$, $L’=L(\alpha)$ とすると、$L’$ も $K’$ のガロア拡大体であり、新しいガロア群 $\Gal{L’/K’}$ は元のガロア群 $\Gal{L/K}$ の部分群と同型。（より詳しくは、$K’$ の「元の拡大体 $L$ の中での正味の拡大」$K’ \cap L$ を $K”$ とするとき、
\[ \Gal{L’/K’} \cong \Gal{L/K”} \]
である）

さて、可解な方程式を解く話に戻ろう。$\Q$ 係数方程式 $f(x)=0$ のガロア群 $G_{0}$ が可解で、組成列
\begin{equation}
\label{eq:howto-new6-4}
G_{0} \rhd G_{1} \rhd \dots \rhd \{1\}
\end{equation}
がわかっているとしよう。組成列は、隣り合う群どうしの要素数比 $\zettaiti{G_{i}}/\zettaiti{G_{i+1}}$ が素数になるよう取ってあるとする。

組成列のうち、着目している隣り合う群が $G$, $H$ だとし、対応する体を $K$, $L$ とする。前回の記事で $K’$ と書いていたものを、ここでは（上の定理に合わせるために）$L$ と書いているので注意。

$\zettaiti{G/H} = \zettaiti{G}/\zettaiti{H} = p$ は素数となり、$\Gal{L/K}$ は $p$ 次巡回群である。$L$ は、$K$ の何らかの数 $A$ の $p$ 乗根 $\sqrt[p]{A}$ を $K$ に添加した体になっている: $L=K(\sqrt[p]{A})$。$A$ は未知であることに注意しよう（$p$ は当然ながら既知）。なお、$K$ が $1$ の原始 $p$ 乗根を含んでいない場合は $\sqrt[p]{A}$ の形の数の添加ではうまく行かないこともあるが、いずれにせよ $K$ に何らかの複素数を添加すると $p$ 次巡回拡大体 $L$ ができることは変わらないので、この添加する複素数を以下 $\sqrt[p]{A}$ と略記してしまう。

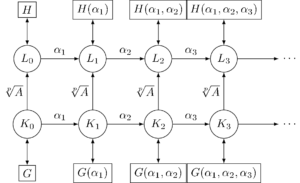
元の $\Q$ 係数方程式 $f(x)=0$ の解を $\alpha_{1}, \alpha_{2}, \dots, \alpha_{n}$ とする。図のように、$K_{0}=K$ に $\alpha_{1}, \alpha_{2}, \dotsc$ を順に添加した体を $K_{1}, K_{2}, \dotsc$ とし、$L_{0}=L$ に $\alpha_{1}, \alpha_{2}, \dotsc$ を順に添加した体を $L_{1}, L_{2}, \dotsc$ とする。これも、前回の記事では $K$, $M$, $L$ と書いていたものがここでは $K_{0}$, $K_{1}$, $K_{2}$ になり、$K’$, $M’$, $L’$ と書いていたものをここでは $L_{0}$, $L_{1}$, $L_{2}$ と書いているので注意してほしい。また、添字 $i$ と $j$ の役割も混同しないでほしい。$i$ は\eqref{eq:howto-new6-4}の組成列の群 $G_{i}$ に対する添字で、この $i$ を固定した上で $G=G_{i-1}$ と $H=G_{i}$ に対応する体 $K$, $L$ に解 $\alpha_{1}, \alpha_{2}, \dotsc$ を順次添加していくときの体 $K_{j}$, $L_{j}$ の添字が $j$ である。

$j=0,1, \dotsc$ のすべてに対し、$L_{j} = K_{j}(\sqrt[p]{A})$ となっている。

ふたつの体の列 $K_{0}, K_{1}, \dotsc$ と $L_{0}, L_{1}, \dotsc$ はどちらもいずれは $f(x)$ の $\Q$ 上の最小分解体となり一致する。$K_{n}=L_{n}$ および $K_{n-1}=L_{n-1}$ は明らか（どちらも最小分解体）だが、場合によっては $j<n-1$ で $K_{j}=L_{j}$ となることもある。その場合、$K_{j}=L_{j}$ となったからと言ってそれらが $f(x)$ の最小分解体になるとは限らないが、一度 $K_{j}=L_{j}$ となればその後の $j$ でもずっと $K_{j}=L_{j}$ となり続けることは明らかだ。

ここで、上の定理を繰り返し適用すると、$\Gal{L_{1}/K_{1}}$ は $\Gal{L_{0}/K_{0}}$ の部分群（と同型）、$\Gal{L_{2}/K_{2}}$ は $\Gal{L_{1}/K_{1}}$ の部分群（と同型）…の繰り返しとなる。$A$ が $B$ の部分群と同型であることを
\[ B \succ A \]
で表すと
\begin{equation}
\label{eq:howto-new6-1}
\Gal{L_{0}/K_{0}} \succ \Gal{L_{1}/K_{1}} \succ \Gal{L_{2}/K_{2}} \succ
\dots
\end{equation}
である。

ところが、\eqref{eq:howto-new6-1}のはじめの $\Gal{L_{0}/K_{0}}$ は $p$ 次巡回群だから、その部分群は $p$ 次巡回群か単位群のいずれかだ。そして、\eqref{eq:howto-new6-1}の最後の $\Gal{L_{n}/K_{n}}$ は単位群である。よって、\eqref{eq:howto-new6-1}は途中まではずっと $p$ 次巡回群で、ある所から先はすべて単位群となる。つまり、次のような番号 $t$ が存在する。
\begin{equation}
\label{eq:howto-new6-2}
\underbrace{\Gal{L_{0}/K_{0}}, \dots, \Gal{L_{t-1}/K_{t-1}}}_{\text{$p$
次巡回群}}, \underbrace{\Gal{L_{t}/K_{t}}, \dots,
\Gal{L_{n}/K_{n}}}_{\text{単位群}}
\end{equation}
これに当たることを、前の記事ではわざわざ第二準同型定理なんてものを使って論じていたが、そんな必要は全然なかったのだ。置換群としての $G$, $H$ が具体的にわかっているという状況で、そのおかげで図の各体に対応する部分群 $G(\alpha)$ 等もすべてわかっていたので、それに気を取られてそういった群を直接見ることしか考えていなかったが、ここでやったように、それらの比 $G/H \cong \Gal{L_{0}/K_{0}}$, $G(\alpha_{1})/H(\alpha_{1}) \cong \Gal{L_{1}/K_{1}}$ 等に着目した方がはるかに簡単に事情がわかったのだ。考えが浅かったというほかない。

話を続けよう。\eqref{eq:howto-new6-2}より
\[ L_{j} = K_{j} \quad (j=t, t+1, \dots, n) \]
で、これは次のことを意味する。$j=0$ から $j=t-1$ までは、$K_{j}$ から上の体 $L_{j}$ に「上がる」ためには $\sqrt[p]{A}$ を添加しなければならないが、$K_{t}$ になったとたんその $\sqrt[p]{A}$ なしで $K_{t}=L_{t}$ となった。これは、$j=t$ にうつるときに添加した $\alpha_{t}$ と $K_{t-1}$ の数を合わせると $\sqrt[p]{A}$ を作れるようになっているということで、言い換えると $\sqrt[p]{A} \in K_{t-1}(\alpha_{t}) = K_{t}$ ということである。

また、\eqref{eq:howto-new6-2}から、$j=t,t+1,\dots,n$ のとき
\begin{gather*}
G(\alpha_{1}, \dots, \alpha_{j}) = H(\alpha_{1}, \dots, \alpha_{j}) = H \cap G(\alpha_{1}, \dots, \alpha_{j}) \\
\therefore G(\alpha_{1}, \dots, \alpha_{j}) \subset H
\end{gather*}
であることもわかる。一方 $j=0,\dots,t-1$ までは $H(\alpha_{1}, \dots, \alpha_{j}) = H \cap G(\alpha_{1}, \dots, \alpha_{j})$ は $G(\alpha_{1}, \dots, \alpha_{j})$ の真部分群だから
\[ G(\alpha_{1}, \dots, \alpha_{j}) \not\subset H \]
である。したがって、$t$ は「初めて $G(\alpha_{1}, \dots, \alpha_{j}) \subset H$ となる $j$」として特徴づけられる。

$K_{t-1}$, $L_{t-1}$, $K_{t}=L_{t}$ の関係を図示すると、こうなっている。

この図と
\[ [L_{t}:K_{t-1}] = [L_{t}:L_{t-1}][L_{t-1}:K_{t-1}] \]
を見比べると、次のことがわかる。

$L_{t-1}$ は $K_{t-1}$ の $p$ 次巡回拡大だったから、$[L_{t-1}:K_{t-1}] = p$ である。
よって、
\begin{equation}
\label{eq:howto-new6-3}
[L_{t}:L_{t-1}] = \frac{1}{p}[L_{t}:K_{t-1}]
\end{equation}
である。
$[L_{t}:L_{t-1}]$ は、「$L_{t-1}$ に $\alpha_{t}$ を添加するときの拡大次数」で、$[L_{t}:K_{t-1}]$ は「$K_{t-1}$ に $\alpha_{t}$ を添加するときの拡大次数」だ。同じ $\alpha_{t}$ を添加しているのに、\eqref{eq:howto-new6-3}は前者の拡大次数の方が後者の拡大次数の $\frac{1}{p}$ 倍に縮小していることを意味する。つまり、$\alpha_{t}$ の最小多項式は、$L_{t-1}$ 成分のものと $K_{t-1}$ 成分のものでは違っており、$\sqrt[p]{A}$ の添加によって後者が因数分解されて、次数が $\frac{1}{p}$ 倍になったものが前者になっている。

このようにして、最小多項式 $g_{\alpha_{1}}(x), g_{\alpha_{2}}(x), \dotsc$ の中で、更新されるのは $g_{\alpha_{t}}(x)$ であることがわかる。$t$ を、いま既知である置換のリストから決定するには、次のようにすればいい。これは以前の記事と同じ手順ではあるが、上で得られた知見と見比べると理解が深まるだろう。

$G(\alpha_{1}), G(\alpha_{1},\alpha_{2}), \dotsc$ を求める。step2 以降なら、前 step での $H(\alpha_{1}), H(\alpha_{1},\alpha_{2}), \dotsc$ がそっくりそのまま使えるので、改めて求める必要はない。
$H(\alpha_{1}) = H \cap G(\alpha_{1}), H(\alpha_{1},\alpha_{2}) = H\cap G(\alpha_{1},\alpha_{2}), \dotsc$ を求める。そして、$H$ との共通部分を取っても変化がない最初の箇所を特定する。
変化があった最後は $G(\alpha_{1},\dots, \alpha_{t-1})$ で、変化が起こらなかった最初は $G(\alpha_{1},\dots, \alpha_{t})$ だ。これらに対応する体どうしの間に添加された解が $\alpha_{t}$ で、その最小多項式が、この step で更新される最小多項式になる。

以下は、以前の記事と同様にすればよい。

投稿日

2021年1月7日

カテゴリー:

ガロア理論, 数学

投稿者:

井汲景太

タグ:

“新・方程式のガロア群の求め方 & ガロア群が可解である方程式の解き方その6” への7件のフィードバック

サイトウ

2022年6月10日

はじめまして。ガロア理論を勉強する中で参考にさせていただいております。大変勉強になります。ありがとうございます。
自分はまだまだ未熟で、とても理論を習得したと言えない身です。なので、質問するなど、超初歩的な内容でもあり申し訳ないのですが、もしお時間があれば是非ともご助言をお願いしたくコメントさせていただきました。

係数体Kから順次べき根拡大を作っていき、ある拡大Ｌになって、K係数方程式の最小分解体Sが、S⊂L　となるとき、方程式は代数的に解け、このとき、S/Kのガロア群は可解群になると思います。
このことを、多くの書物は、Lを含む大きなKのガロア拡大を作り、そのガロア群の商群として、S/Kのガロア群の可解性を証明していると思われます。（私の間違いでなければ）
ですが、ガロアは（当時の手法とはもちろん異なると思いますが）、結果的には、根の有理式を添加していけばよく（代数的可解性の原則？）、最小分解体のガロア群の可解性を直接引き出しているように思われます。商群としての可解性を言うのではなくて。L=Sとみなしているとも言えるかもしれません。実際、L=Sとしている書物もあり、ごまかしているのか、あるいは、そのようにしても差し支えないのか、混乱します。
１のｎ乗根の扱いに大きく関係しているのかも知れません。と言うことで、恥ずかしながら、いまだにこの最後の詰めのところが釈然としません。
上手く表現出来ずたいへん申し訳ありませんが、可能であればご助言などご教示いただけますとありがたく思います。よろしくお願いいたします。すみません。

返信
1. 井汲景太
  
  2022年6月10日
  
  コメント・ご質問ありがとうございます。お役に立てているようでなによりです。
  ・ $L=S$ なのかどうか
  私も以前引っ掛かっていた点です。混乱しますよね。結論から言えば $L=S$ とは限らず、一般には $L \supset S$ しかなりたちません（方程式によっては $L=S$ となることもあります）。
  非自明でわかりやすい例として、角の 3 等分方程式 $x^3-3x+1=0$ を考えてみます。解は $\alpha=2\cos(40^\circ)$, $\beta=2\cos(160^\circ)$, $\gamma=2\cos(280^\circ)$ です。$1$ の原始 $3$ 乗根を $\omega=\frac{-1 + \sqrt{-3}}{2}$ とすると、解は
  \begin{align*}
  \alpha &= \sqrt[3]{\omega} + \sqrt[3]{\omega^2} \\
  \beta &= \omega\sqrt[3]{\omega} + \omega^2\sqrt[3]{\omega^2} \\
  \gamma &= \omega^2\sqrt[3]{\omega} + \omega\sqrt[3]{\omega^2}
  \end{align*}
  となります（3乗根の枝は適切に取るものとします）。よって、$\mathbb{Q}$ にべき根を順次添加して解く場合はまず $\sqrt{-3}$ を添加して $\omega$ が使えるようにし、次に $\sqrt[3]{\omega}$ を添加するという流れになります。
  \[ L = \mathbb{Q}(\sqrt{-3}, \sqrt[3]{\omega}) \]
  この拡大次数は、まず $\sqrt{-3}$ の添加が $2$ 次拡大で、さらに $\sqrt[3]{\omega}$ の添加が $3$ 次拡大ですから、$6$ 次拡大になります。
  \[ [L:\mathbb{Q}] = [L:\mathbb{Q}(\sqrt{-3})][\mathbb{Q}(\sqrt{-3}):\mathbb{Q}] = 3 \cdot 2 = 6 \]
  一方、最小分解体 $S = \mathbb{Q}(\alpha, \beta, \gamma)$ の方の拡大次数は、$S=\mathbb{Q}(\alpha)$ であることから $3$ 次拡大です。
  \[ [S:\mathbb{Q}] = [\mathbb{Q}(\alpha):\mathbb{Q}] = 3 \]
  したがって $L \ne S$ で、$L$ は $S$ よりも真に大きい体です。
  こんな風に、「べき根のみを添加していく」という制限を付けるとき、一般に、最小分解体にぴったり一致する体が作れるとは限らず、最小分解体を含むより広い体しか作れないことはありうるわけです。
  ・ガロアの手法との関係
  私もガロアの原論文にちゃんと当たったわけではないですが、私が読んだ文献の記述から、私は次のように理解しています。
  ガロアの時代は、$1$ のべき根に限ればすべてべき根で表せるということがガウスによってわかっていました（$3$乗根 $\frac{-1+\sqrt{-3}}{2}$, $4$ 乗根 $\sqrt{-1}$, $5$ 乗根 $\frac{1}{2}\biggl( \frac{-1+\sqrt{5}}{2} + \sqrt{\frac{-5-\sqrt{5}}{2}} \biggr)$…）
  このことから、ガロアの考察においては、「使用可能な数」として有理数と「$1$ のべき根」の区別ははっきりつけておらず、$p$ 乗根の添加に当たっては「今まで $\mathbb{Q}$ だと思っていた係数体は、実は $1$ の原始 $p$ 乗根を含んでいたということにするよ」みたいな考え方に当たるようなルーズな扱い方をしています。
  ですから、$V$ の最小多項式が $1$ 次式にまでに因数分解し尽くした時の体は、現代の厳密な視点では一般には最小分解体ではなく、余裕のあるより大きい体になっている…というわけです。つまりガロアが示したことも、現在の記法で言えば $L=S$ ではなく $L \supset S$ です。
  
  返信
サイトウ

2022年6月12日

ご教示感謝申し上げます。とても丁寧なご説明でよくわかりました。ありがとうございます。
非自明な例として、120°の三等分方程式がとても分かり易かったです。この方程式をカルダノの方法で解くとωを使ってキレイな形に書けるんですね。いつも三角関数解でしか考えていなかったので、恥ずかしながら勉強になりました。

この方程式のＳ＝Ｑ（α、β、γ）=Q(α)は、Q上3次のガロア拡大であり、そのガロア群は３次の巡回群です。なので、可解群であり代数的に解けることになります。しかしながら、実際に代数的に解くためにはωが必要であるため、Qにωを添加し2×3=6次の拡大を作る必要があり、Q⊂Ｑ(ω)⊂Q(ω、α)＝Ｑ(√-3、ω^(1/3)) 、ω^(1/3)=α+ω^2β+ωγ

↑の過程ですが、正解しているでしょうか？可解群であれば代数的に解けるとはいうものの、実際には１のｎ乗根が必要となり、事前に用意しておく必要があると言う認識で良いでしょうか？
ちなみに、この場合、Q⊂Q(α)⊂Q(α、ω)のルートではダメですよね。(α+ω^2β+ωγ)^3は3次の巡回群で不変であっても、そもそもα+ω^2β+ωγ　がQ(α)の元ではないので。
いろいろと初歩的なことばかりで申し訳ありません。

返信
井汲景太

2022年6月12日

＞ ↑の過程ですが、正解しているでしょうか？
OK です。（α+ω^2β+ωγ は $\omega^{1/3}$ ではなく $3\omega^{1/3}$ ですが）
＞実際には１のｎ乗根が必要となり、事前に用意しておく必要があると言う認識で良いでしょうか？
うーんと、「事前に用意しておく必要がある」というのがどういうことなのかよくわかりません。前回書いた通り、1の原始 $n$ 乗根はすべてべき根で表せるので、1のべき根の添加は、その気になればすべて（多段の）べき根添加で代替できますよ。例えば $1^{1/3}$ は $\sqrt{-3}$ の添加で作れますし、$1^{1/5}$ は $\sqrt{5}, \sqrt{-10-2\sqrt{5}}$ を順次添加すれば作れる…といった具合です。
＞ Q⊂Q(α)⊂Q(α、ω)のルートではダメですよね。
そうなります。

返信
サイトウ

2022年6月19日

お礼が遅れてすみません。ご回答ありがとうございました。そうでした、ωの３乗根に係数が落ちてました。話は変わるのですが、

昨年、東工大のＫ先生が（オンライン上の）ｎ予備校でガロア理論のオンライン講義をされており、その講義の中で（テキストの中で）、次のことを言われてます。

ア　FをQ の拡大体とし，F上の n 次代数方程式 f(x) = 0 の最小分解体を Eとする。また，F は 1 の原始 n! 乗根を含むとする。このとき，f(x) = 0
が代数的に可解であるための必要十分条件は，ガロア群 G = Gal(E/F) が可解群であることである
————————————–
ここでは，代数方程式の代数的可解性とガロア群の可解性とが同値であることを「考えている基礎体F が十分に多くの1 のべき根を含む」という追加条件のもとに説明した。実は，この追加条件は必要ないことが知られている。つまり，次の定理が成り立つ（証明は省略する）。
————————————–
イ　FをQの拡大体とし，F上のn 次代数方程式f (x) = 0 の最小分解体をE
とする。このとき， f (x) = 0 が代数的に可解であるための必要十分条件
は，ガロア群G = Gal(E/F) が可解群であることである。

勉強不足なため、どうもこのあたりがすっきりしません。そこで、
①ア、イを例の角の三等分方程式f(x)=0で言うと、
Q上S=Q(α、β、γ)のガロア群の可解性は、Q⊂Q(√ー3)⊂Q(√ー3、α)=Lとガロア拡大を重ね、L/Qの中間体として（Gal(L/Q)の商群）として示すことになるのでしょうか？
②アをイに読み替える？必要性はそもそもなぜなのでしょうか？代数的可解性の条件を方程式の係数とその根から定まる最小分解体の条件にシンプルに落とし込むためなのでしょうか？

意味不明な部分も多々あるかと思いますが、少しでもご助言等いただけますと幸いです。申し訳ございません。

返信
井汲景太

2022年6月19日

加藤文元さんのガロア理論講義、勤め先のツテでざっと見てはいます。以下、体の拡大を $\mathbb{Q} \to \mathbb{R} \to \mathbb{C}$ のように矢印で表し、また、添加する数を明記して $\mathbb{Q} \xrightarrow{\sqrt{2}} \mathbb{Q}(\sqrt{2})$ のように書いたりもします。
①について:
一般に、次のことがなりたちます。
体の拡大 $A \to B \to C$ があるとする。$A \to B$, $B \to C$ がともに可解拡大で、かつ $A \to C$ がガロア拡大でもあるとき、$A \to C$ は可解拡大…☆

さて、$n$ 次有理数係数方程式 $f(x)=0$ がべき根で表せる解 $\alpha, \beta, \dots, \gamma$ を持つとし、$1$ の原始 $n!$ 乗根を $\zeta$ としましょう。ここで考えたいのは、
\[ \mathbb{Q} \xrightarrow{\zeta} \mathbb{Q}(\zeta) \xrightarrow{\alpha, \dots, \gamma} \mathbb{Q}(\zeta, \alpha, \dots, \gamma) \]
という拡大です。べき根で表せる解を持つので、後半の $\alpha, \beta, \dots, \gamma$ を添加する拡大は、「ア」によって可解拡大です。一方、前半の $\zeta$ を添加する拡大もやはり可解拡大です（加藤さんの資料だと補題 1.3.1）。よって、先ほどの☆から、全体としての拡大 $\mathbb{Q} \to \mathbb{Q}(\zeta, \alpha, \dots, \gamma)$ も可解拡大です。したがって、その部分拡大となるガロア拡大 $\mathbb{Q} \xrightarrow{\alpha, \dots, \gamma} \mathbb{Q}(\alpha, \dots, \gamma)$ も可解拡大です。（これは、加藤さんの資料の「ガロア理論の基本定理(5)」及び「可解群の商群は必ず可解群」という性質から）
今、同値性「群が可解群」$\Leftrightarrow$「べき根で解ける」について考えているわけですが、「$\impliedby$」の方は今のようにして「ア」によって「イ」が示せます。一方、「$\implies$」の方はもうちょっと非自明で、それが②の話にも関わってきます。
一旦ここで切ります。

返信
井汲景太

2022年6月20日

②について:
まず、これまでも $1$ の $n$ 乗根はすべてべき根で表せる、と書いてきましたが、これは自明なことではありません。$p$ を素数とするとき、$1$ の原始 $p$ 乗根は $x^{p-1}+x^{p-2}+ \dots + 1=0$ の解ですから、$p$ が大きくなると、この方程式がべき根で解けるかどうか、次数だけでは定かでなくなってきます。
「ア」と「イ」を区別しているのは、「$1$ の $n$ 乗根がべき根で表せる」という事実抜きでは、一般の方程式に対して、何を以て「べき根で解ける」と言うかが変わってくるからです。
極端な場合として、$1$ の原始 $3$ 乗根 $\omega$ がべき根で表せなかったとしてみましょう（「$x^2+x+1=0$ は $2$ 次方程式だから表せないはずがない」という話は一旦おいておき、この方程式が「べき根では解けない」方程式だったとして話を進めます）。このとき、$x^3=2$ という方程式の解は $\sqrt[3]{2}$, $\sqrt[3]{2}\omega$, $\sqrt[3]{2}\omega^2$ ですが、これは「べき根で表せた」と言えるかどうか、議論の余地があります。つまり、
\begin{gather*}
\sqrt[3]{2}, \sqrt[3]{2}\omega, \sqrt[3]{2}\omega^2 \\
\text{ただし}\omega\text{は}\omega^2+\omega+1=0\text{をみたす数で、これ以上簡単には表せない}
\end{gather*}
というのが解の表現になりますから、第一の解 $\sqrt[3]{2}$ 以外は「べき根だけで表せた、とは言い難い」という見方がありえます。
この場合は、解の別の表し方として
\begin{gather*}
\sqrt[3]{2}, \sqrt[3]{2}’, {\sqrt[3]{2}}^{\prime\prime} \\
\text{ただし、}a\text{の3乗根の3つの枝を}\sqrt[3]{a}, \sqrt[3]{a}’, \sqrt[3]{a}^{\prime\prime}\text{とする}
\end{gather*}
というものがありますから、「解がべき根で表せる」ケースに含まれる、という見方もあるでしょう。
続いて、$x^3-3x+1=0$ を考えます。解は、前者の表記では
\begin{align*}
\alpha &= \sqrt[3]{\omega} + \sqrt[3]{\omega^2} \\
\beta &= \omega\sqrt[3]{\omega} + \omega^2\sqrt[3]{\omega^2} \\
\gamma &= \omega^2\sqrt[3]{\omega} + \omega\sqrt[3]{\omega^2} \\
\text{ただし}&\omega\text{は}\omega^2+\omega+1=0\text{をみたす数}
\end{align*}
で、後者でも
\begin{align*}
\alpha &= \sqrt[3]{\sqrt[3]{1}’} + \sqrt[3]{\sqrt[3]{1}^{\prime\prime}} \\
\beta &= \sqrt[3]{\sqrt[3]{1}’}’ + \sqrt[3]{\sqrt[3]{1}^{\prime\prime}}^{\prime\prime} \\
\gamma &= \sqrt[3]{\sqrt[3]{1}’}^{\prime\prime} + \sqrt[3]{\sqrt[3]{1}^{\prime\prime}}’
\end{align*}
となります。これは、個人差もあるでしょうが、「べき根で表せた」という感じはしない、という人が多いんじゃないでしょうか。（もっとも、$1$ の原始 $4$ 乗根を「それ以上書き表しようがない」から $i$ と書いて、$x^2=-2$ の解を $\pm \sqrt{2}i$ と書いたものは「べき根で表せた」と言うのが普通の感覚ですから、結局は慣れの問題で、上のどちらも「べき根で表した解」の範疇に入っている、という考え方もあるでしょうが）
話を戻すと、「ア」の「$\implies$」の方が言っているのは、「$x^3-3x+1=0$ の解が
\begin{align*}
\alpha &= \sqrt[3]{\omega} + \sqrt[3]{\omega^2} \\
\beta &= \omega\sqrt[3]{\omega} + \omega^2\sqrt[3]{\omega^2} \\
\gamma &= \omega^2\sqrt[3]{\omega} + \omega\sqrt[3]{\omega^2} \\
\text{ただし}&\omega\text{は1の原始3乗根}
\end{align*}
と表せる」ということ止まりで、$\omega$ の素性についてはそれ以上何も追究していません。別に、$\omega$ 自身はべき根で表せなくたっていいのです。一方、「イ」の「$\implies$」の方は但し書き抜きの
\begin{align*}
\alpha &= \sqrt[3]{\frac{-1+\sqrt{-3}}{2}} + \sqrt[3]{\frac{-1-\sqrt{-3}}{2}} \\
\beta &= \frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{-1+\sqrt{-3}}{2}} + \frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{-1-\sqrt{-3}}{2}} \\
\gamma &= \frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{-1+\sqrt{-3}}{2}} + \frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{-1-\sqrt{-3}}{2}}
\end{align*}
という形に書ける、ということまで言っています。
繰り返しますが、$1$ の $n$ 乗根はすべてべき根で表せるので、その予備知識を前提とすれば「ア」と「イ」の「$\implies$」に違いはありません。ただそれが自明でないため、加藤さんは「ア」と「イ」をきちんと区別して書いていたわけです。

返信

コメントを残すコメントをキャンセル

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。

新・方程式のガロア群の求め方 & ガロア群が可解である方程式の解き方 その6

コメント

“新・方程式のガロア群の求め方 & ガロア群が可解である方程式の解き方 その6” への7件のフィードバック

コメントを残す コメントをキャンセル

新・方程式のガロア群の求め方 & ガロア群が可解である方程式の解き方その6

“新・方程式のガロア群の求め方 & ガロア群が可解である方程式の解き方その6” への7件のフィードバック

コメントを残すコメントをキャンセル