\(\newcommand{\Q}{\mathbb{Q}}\renewcommand{\dotsc}{\cdots}\newcommand{\zettaiti}[1]{\lvert #1 \rvert}\)先日の記事で可約な方程式の解を実際にべき根で求める手順では、step2 では、一旦原始元 \(u\) に関する処理に還元し、また新しい \(g_{\beta}(x)\) の算出には一般には多項式の GCD 計算を用いる、という流れになっていた。しかし、その後色々考察を進めた結果、これはまだ無駄のある方針だった。せっかくのガロア理論の教えを私は十分に生かせておらず、その核心部「中間体と部分群の1体1対応」への眼差しが不十分だった。ここでは、GCD 計算なしで \(g_{\beta}(x)\) を求める手順を説明する。さらに、より一般に全 step を通じて \(g_{\alpha}(x), g_{\beta}(x), g_{\gamma}(x), \dotsc\) のどれがその step での既約分解対象になるかということも、一貫性のある形で早い段階で特定できることもわかった。
以下説明する。
先日の記事の例をそのまま使う。ただし、そこでは \(G\) と \(G_{0}\) を共に「\(\Q\) 上のガロア群」の表記として使っていたが、ここでは文字 \(G\), \(H\) は「組成列の途中の任意の隣り合う群」を表す文字として後の方で使いたいので、「\(\Q\) 上のガロア群」の表記は \(G_{0}\) のみとする。
まず、組成列は次の通りだった。
\begin{gather*}
G_{0} \supset G_{1} \supset G_{2} \supset \{\sigma_{1}\} \\
G_{0} = \{\sigma_{1}, \sigma_{2}, \sigma_{3}, \sigma_{4}, \sigma_{5}, \sigma_{6}, \sigma_{7}, \sigma_{8}, \sigma_{9}, \sigma_{9}, \sigma_{10}, \sigma_{11}, \sigma_{12} \} \\
G_{1} = \{ \sigma_{1}, \sigma_{2}, \sigma_{5}, \sigma_{6}, \sigma_{9}, \sigma_{10} \} \\
G_{2} = \{ \sigma_{1}, \sigma_{6}, \sigma_{9} \}
\end{gather*}
続いて、解の一部を添加した体と群の対応を確認しておこう。\(\Q(\alpha)\) に対応する部分群は、\(G_{0}\) の元のうち \(\alpha\) を固定するものの群、すなわち \(G_{0}\) の \(\alpha\) 固定部分群だから \(G_{0}(\alpha) = \{\sigma_{1}, \sigma_{2}\}\) である。この例では \(2\) 根添加で最小分解体ができていたことも合わせ、次のようにまとめられる。
\begin{align*}
\Q &\leftrightarrows G_{0} \\
\Q(\alpha) &\leftrightarrows \{\sigma_{1}, \sigma_{2}\} \\
\Q(\alpha, \beta) &\leftrightarrows \{\sigma_{1}\} \quad \text{(単位群)}
\end{align*}
では、新しい考え方で step1 から改めてやり直してみよう。組成列の始めの2つの群を \(G=G_{0}\), \(H=G_{1}\) とおく。\(p= \zettaiti{G/H} =2\) である。\(G\), \(H\) に対応する体を \(K\), \(K’\) とすると、\(K=\Q\) である。\(K’\) の方は実は \(\Q(\sqrt{2})\) になるが、そのことはこの時点ではまだわからず、\(K\) の \(p=2\) 次巡回拡大であることだけがわかっている。
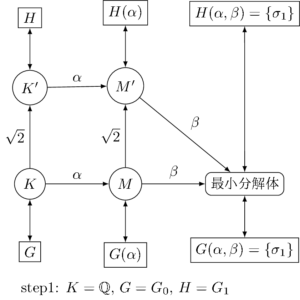
\(K\), \(K’\) にそれぞれ \(\alpha\) を添加した体を \(M=K(\alpha)\), \(M’=K'(\alpha)\) とする。\(M\), \(M’\) に \(\beta\) を添加すると、いずれも最小分解体(\(\Q(\alpha, \beta)\))ができる。
\(M\), \(M’\) に対応する群はそれぞれ \(G\) と \(H\) の \(\alpha\) 固定部分群 \(G(\alpha)\), \(H(\alpha)\) で、具体的には
\begin{align*}
G(\alpha) &= G_{0}(\alpha) = \{\sigma_{1}, \sigma_{2}\} \\
H(\alpha) &= H \cap G(\alpha) = G_{1} \cap \{\sigma_{1}, \sigma_{2}\} = \{\sigma_{1}, \sigma_{2}\}
\end{align*}
である。\(H(\alpha) = G(\alpha)\) より \(M’=M\) であり、「\(\alpha\) の添加による拡大次数」、つまり \([M:K]\) や \([M’:K’]\) が、べき根(\(\sqrt{2}\))の添加によって減少していることがわかる。これは、べき根の添加によって \(\alpha\) の最小多項式の次数が減少している、ということだ。新しい拡大次数は
\[ [M’:K’] = \frac{\zettaiti{H}}{\zettaiti{H(\alpha)}} = \frac{6}{2} = 3 \]
である。別の言い方をすれば、「べき根の添加によって \(g_{\alpha}(x)\) の次数が \(\frac{1}{p}=\frac{1}{2}\) 倍に縮小している」ということになる。
したがって \(g_{\alpha}(x)\) は新しい体 \(K’\) では \(p=2\) 個の \(3\) 次式に既約分解され、そのそれぞれは \(H\) 不変である。
\[ g_{\alpha}(x) = \underbrace{(x-\alpha_{1}) (x-\alpha_{3}) (x-\alpha_{5})}_{H\text{で不変}} \times \underbrace{(x-\alpha_{2}) (x-\alpha_{4}) (x-\alpha_{6})}_{H\text{で不変}} \]
ここから、\(K\) に添加すべきべき根(\(2\sqrt{2}\))と \(\alpha\) の新しい最小多項式 \(g_{\alpha}(x) = x^{3}+\sqrt{2}\) を求める計算は以前の記事と同じなので省略する。
続いて、step2 を考える。今度は、組成列の隣り合う群は \(G=G_{1}\), \(H=G_{2}\) である。今度も \(p = \zettaiti{G/H} = 2\) である。\(G\), \(H\) に対応する体を \(K\), \(K’\) とすると、今度の \(K\) は先ほどの step1 での \(K’\) で \(K=\Q(\sqrt{2})\) である。\(K’\) は \(K(\sqrt{-6})\) になるが、そのことはこの時点ではまだわからず、\(K\) の \(p=2\) 次巡回拡大であることだけがわかっている。

step1 と同様に \(M\), \(M’\) を定め、それらと対応する群を \(G(\alpha) = G_{1}(\alpha) = \{\sigma_{1}, \sigma_{2}\}\), \(H(\alpha) = H \cap G_{1}(\alpha) = \{\sigma_{1}\}\) とおく。\(G\) はさっきの step1 での \(H\) だから、今度の \(G(\alpha)\) はもちろん step1 での \(H(\alpha)\) そのものである。
step1 と違って、\(G(\alpha)\) は \(H\) との共通部分をとることにより真に縮小しており(\(H(\alpha)\) になった)、\(M’\) は \(M\) の \(p=2\) 次巡回拡大になっている。したがって、 \(K\) から \(M\) への拡大次数は \(K’\) から \(M’\) になっても変わらず、\(\alpha\) の最小多項式の次数は変わらない。すなわち \(g_{\alpha}(x)\) は不変である。
一方、\(\alpha\), \(\beta\) を共に固定する固定部分群 \(G(\alpha,\beta)\), \(H(\alpha, \beta)\) は当然どちらも最小分解体に対応する群で単位群 \(\{\sigma_{1}\}\) になる。したがって、\(M\) から最小分解体への拡大次数が、べき根の添加によって減少している。\(M’\) から最小分解体への拡大次数は
\[ \frac{\zettaiti{H(\alpha)}}{\zettaiti{H(\alpha,\beta)}} = \frac{1}{1} = 1 \]
である(つまり、\(M’\) は最小分解体である)。また、\(G(\alpha)/H(\alpha)\) は \(p=2\) 次巡回群であり、\(G(\alpha)-H(\alpha)\) の任意の元——今の場合は \(\sigma_{2}\) のみ——(から作られる剰余類)がその生成元になっている。
よって、\(g_{\beta}(x)\) は新しい体 \(M’\) では \(p=2\) 個の \(1\) 次式に既約分解され、そのそれぞれは \(H(\alpha)\) 不変である。
\[ g_{\beta}(x) = \underbrace{(x-\alpha_{3})}_{H(\alpha)\text{で不変}} \times \underbrace{(x-\alpha_{5})}_{H(\alpha)\text{で不変}} \]
これに基づき、\(h_{i}(x)\), \(\theta_{i}(x)\) を改めて
\begin{align*}
h_{1}(x) &= x-\alpha_{3} = x-\beta \\
h_{2}(x) &= x-\alpha_{5} = x+\alpha+\beta \\
\theta_{1}(x) &= h_{1}(x) + (-1)^{1}h_{2}(x) = -\alpha-2\beta \\
\theta_{2}(x) &= h_{1}(x) + h_{2}(x) = 2x+\alpha
\end{align*}
とおこう。\(\theta_{i}(x)\) の定め方から、その任意の係数は、\(G(\alpha)/H(\alpha)\) の生成元 \(\sigma_{2}\) で \((-1)^{-i}\) 倍される。
さて、ここまで来たところでひとつ困ったことが起きている。step1 と同様、\(\theta_{1}(x) = -\alpha-2\beta\) を \(p=2\) 乗して次数下げすると
\[ (-\alpha-2\beta)^{2} = \alpha^{2}+4\alpha\beta + 4\beta^{2} = -3\alpha^{2} \]
となり、未知数 \(\alpha\) が消えずに残ってしまう。これでは、添加すべきべき根の値がわからない。どうしてこんなことになってしまったかと言うと、\(G(\alpha)\) は \(K\) ではなく \(M\) 上のガロア群なので、\(G(\alpha)\) で不変という条件だけだと、\(K\) の元とは限らず \(M\) の元になってしまうことがありうるからだ。つまり、元々 \(\theta_{1}(x)\) は \(p=2\) 乗したとき \(M\) の元になることしか保証されない作り方をしている。
そこで、先日の記事と同様に原始元を作る。原始元は、一般には必ずしも \(\Q\) を最小分解体に拡大できるものである必要はなく、今着目している群 \(G\) に対応する体 \(K\) を最小分解体にまで単拡大で拡大できる元 \(u\) を使えば十分だ。ここでは、先日の記事と同じく、\(u=\alpha-\beta\) が使える。これらを、\(G=G_{1}\) の \(6\) つの元で変換するとこうなっていた。
\begin{align*}
u_{1} &= \sigma_{1}(u) = u = \alpha-\beta \\
u_{2} &= \sigma_{2}(u) = 2\alpha+\beta \\
u_{5} &= \sigma_{5}(u) = \beta-\alpha \\
u_{6} &= \sigma_{6}(u) = \alpha + 2\beta \\
u_{9} &= \sigma_{9}(u) = -2\alpha-\beta \\
u_{10} &= \sigma_{10}(u) = -\alpha-2\beta
\end{align*}
これらから、\(H=G_{2}\) では不変だが \(G=G_{1}\) では不変でない多項式として次のものが作れた。
\begin{align*}
\hat{h}_{1}(x) &= (x-u_{1}) (x-u_{6}) (x-u_{9}) \\
&= (x-\alpha+\beta) (x-\alpha-2\beta) (x+2\alpha+\beta) \\
&= x^{3} + 6\alpha^{2}\beta – 3\sqrt{2} \\
\hat{h}_{2}(x) &= (x-u_{2}) (x-u_{5}) (x-u_{10}) \\
&= x^{3} + 6\alpha\beta^{2} – 3\sqrt{2} = x^{3} – 6\alpha^{2}\beta + 3\sqrt{2}
\end{align*}
さらにここから
\[ \hat{\theta}(x) = \hat{h}_{1}(x) + (-1)^{1}\hat{h}_{2}(x) = 12\alpha^{2}\beta – 6\sqrt{2} \]
が作れた。この最高次の係数(やはり今の場合は定数項しかないが)を \(\hat{a}\) とおく。簡単のため、\(6\) で割ったものを \(\hat{a}\) としておこう。
\[ \hat{a}=2\alpha^{2}\beta – \sqrt{2} \]
ここで、\(p=2\) 次巡回群 \(G/H \cong G(\alpha)/H(\alpha)\) の生成元として、共通の \(\sigma_{2}\) が取れる(正確には、\(\sigma_{2}\) から作られる剰余類 \(\sigma_{2}H\) および \(\sigma_{2}H(\alpha)\) がそれぞれの生成元になる)ことに注意すると、先ほどの \(\theta_{1}(x)\) と \(\hat{a}\) は \(\sigma_{2}\) に対して同じ変換性を持つ。つまり、いずれも \(\sigma_{2}\) によって \(-1\) 倍になる。これは、つぎのふたつのことを意味する。
- \(\hat{a}\) は、先日の記事通り \(p=2\) 乗すれば \(K\) の数(\(M\) ではない)になる。
\[ \hat{a}^{2} = 4\alpha^{4}\beta^{2} – 4\sqrt{2}\alpha^{2}\beta + 2
= -6 \] - \(\theta_{1}(x)\) と \(\hat{a}\) の比は \(G(\alpha)\) で不変、すなわち
\begin{equation}
\label{eq:howto-new5-1}
\theta_{1}(x) = \hat{a} \eta_{1}(x)
\end{equation}
とおけば \(\eta_{1}(x)\) は \(M\) の数を元とする多項式になる。
この \(\eta_{1}(x)\) は、前回の記事の3つ目の話題とほぼ同じ考え方を通じて、簡単な係数比較で求められる。やってみよう。
\eqref{eq:howto-new5-1}の両辺は
\[ \{1, \beta\} \]
を基底とする \(M\) 係数 \(1\) 次結合で表されるので、基底のうち適当なひとつについての係数を比べるだけで \(\eta_{1}(x)\) が求められる。今の場合は、\eqref{eq:howto-new5-1}はこんな式だ。
\[ -\alpha-2\beta = (2\alpha^{2}\beta – \sqrt{2}) \eta_{1}(x) \]
したがって、基底 \(\{1, \beta\}\) の係数を比較することで次の2つの式が得られる。
\[ -\alpha=-\sqrt{2}\eta_{1}(x), \quad -2=2\alpha^{2}\eta_{1}(x) \]
当然ながら両者は同値で、いずれからも \(\eta_{1}(x) = \frac{\alpha}{\sqrt{2}}\) と \(\eta_{1}(x)\) が決定できる(だから、2つの式を両方導く必要はなく、実際には片方だけ導けば必要な計算はできる)。これと \(\hat{a}=\sqrt{-6}\) であったことから、
\[ \theta_{1}(x) = \hat{a} \eta_{1}(x) = \sqrt{-6} \frac{\alpha}{\sqrt{2}} \]
と求まり、よって
\[ h_{1}(x) = \frac{\theta_{1}(x)+\theta_{2}(x)}{2} = \frac{1}{2}\Bigl( \sqrt{-6} \frac{\alpha}{\sqrt{2}} + 2x + \alpha \Bigr) \]
となる。これが新しいべき根 \(\sqrt{-6}\) を添加した体 \(M’=M(\sqrt{-6})\) 上の \(\beta\) の新しい最小多項式 \(g_{\beta}(x)\) である。
\[ g_{\beta}(x) = x + \frac{1}{2}\Bigl( \frac{\sqrt{-6}}{\sqrt{2}} + 1 \Bigr)\alpha \]
これは前回の記事で導いた \(g_{\beta}(x) = 2\alpha^{2}x-\sqrt{2}-\sqrt{-6}\) と定数倍の違いしかなく、正しい結果が出ていることがわかる。
最後に、step3 を考える。今度は、組成列の隣り合う群は \(G=G_{2}\), \(H=\{\sigma_{1}\}\) であり、\(p = \zettaiti{G/H} = 3\) である。\(G\), \(H\) に対応する体を \(K\), \(K’\) とすると、今度は \(K=\Q(\sqrt{2}, \sqrt{-6})\) である。\(K’\) は \(K \subset K’ \subset K(\omega, \sqrt[3]{\sqrt{3}})\) となるが、そのことはこの時点ではまだわからず、\(K\) の \(p=3\) 次巡回拡大であることだけがわかっている。
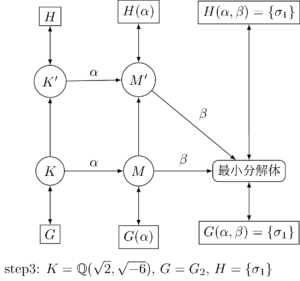
これまでと同様に \(M\), \(M’\) を定め、\(G(\alpha) = G_{2}(\alpha) = \{\sigma_{1}\}\), \(H(\alpha) = H \cap G_{2}(\alpha) = \{\sigma_{1}\}\) とおく。
すると、step1 と同じく \(G(\alpha) = H(\alpha)\) より \(M’=M\) であり、\(K\) から \(M\) への拡大次数が、\(K’\) と \(M’\) になると \(\frac{1}{p} = \frac{1}{3}\) 倍に減少していることがわかる。さらに \(H=H(\alpha) = \{\sigma_{1}\}\) だから \(K’=M’\) でもある。
したがって \(g_{\alpha}(x) = x^{3}+\sqrt{2}\) は新しい体 \(K’\) では \(p=3\) 個の \(1\) 次式に既約分解され、そのそれぞれは \(H\) 不変である。
\[ g_{\alpha}(x) = \underbrace{(x-\alpha_{1})}_{H\text{で不変}} \times \underbrace{(x-\alpha_{3})}_{H\text{で不変}} \times \underbrace{(x-\alpha_{5})}_{H\text{で不変}} \]
ここから、\(K\) に添加すべきべき根(\(\omega\), \(\sqrt[3]{\sqrt{2}}\))と新しい \(g_{\alpha}(x) = x + \sqrt[3]{\sqrt{2}}\) を求める計算は、以前の記事と同じなので省略する。
一般化
今の具体例で、計算がうまく行ったことの事情は、——特に step2 が——上の計算からはわかりにくい。これは、\(p=2,3\) が小さいことと、最小分解体に至る逐次拡大 \(\Q \rightarrow \Q(\alpha) \rightarrow \Q(\alpha,\beta)\) が短いために、どこまでが偶然でどこまでが必然なのか見分けがつきにくいからだ。一般論が見やすいように、\(p\) は文字のままとし、最小分解体は \(3\) 解添加が必要な場合で説明しよう。これまでと同様、添加する解 \(\alpha\), \(\beta\), \(\gamma\) の最小多項式を \(g_{\alpha}(x)\), \(g_{\beta}(x)\), \(g_{\gamma}(x)\) とする。
ガロア群の組成列のうち、着目している隣り合う群が \(G\), \(H\) だとし、対応する体を \(K\), \(K’\) とする。\(H\) は \(G\) の正規部分群で \(\zettaiti{G/H} = p\) は素数となる。\(K’\) は \(K\) の \(p\) 次巡回拡大であるが、\(K\) に何を添加すれば \(K’\) になるかはまだ不明である。
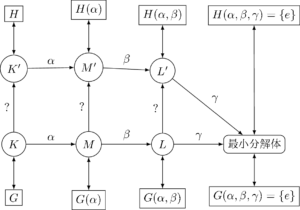
図のように、\(M=K(\alpha)\), \(L=M(\beta)\), \(M’=K'(\alpha)\), \(L’=M'(\beta)\) とする。\(L(\gamma) = L'(\gamma)\) は最小分解体である。対応するガロア群 \(G(\alpha)\) などは図の通り。これらの群はすべて先ほどの例のように \(\sigma_{i}\) のリストの形でわかっているとしてよい。
まず、\(H\) が \(G\) の正規部分群、\(G(\alpha)\) が \(G\) の部分群であることから \(H(\alpha) = H \cap G(\alpha)\) は \(G(\alpha)\) の正規部分群、\(G(\alpha)H\) は \(G\) の部分群で \(H\) はその正規部分群となるが、ここで群の第二準同型定理を思い出すと
\[ G(\alpha) / (H \cap G(\alpha)) \cong (G(\alpha)H) / H \]
である。一方 \((G(\alpha)H) / H\) は \(G/H\) の部分群だが、\(G/H\) は \(p\) 次巡回群だから、その部分群は単位群か \(G/H\) 自身のいずれかだ。以上のことから、\(G(\alpha)/H(\alpha) = G(\alpha) / (H \cap G(\alpha))\) は単位群か \(p\) 次巡回群のどちらかの可能性しかない。
前者なら \(H(\alpha) = G(\alpha)\) だから \(M’=M\) となり、\([M’:K’]\) は \([M:K]\) の \(\frac{1}{p}\) 倍になる(\(\because [M’:K] = [M’:K’]\underbrace{[K’:K]}_{p} = \underbrace{[M’:M]}_{1}[M:K]\))。これが上の例の step1 や step3 で起きていたことだ。
一方後者なら、拡大 \(K \to K’\), \(M \to M’\) が共に \(p\) 次拡大だから、\([M’:K’]=[M:K]\) である(\(\because [M’:K] = [M’:K’]\underbrace{[K’:K]}_{p} = \underbrace{[M’:M]}_{p}[M:K]\))。上の例の step2 はこちらだった。
したがって、どちらになるかは結局 \(G(\alpha) \subset H\) かどうかで判定でき、これによって \(g_{\alpha}(x)\) が変化するかどうかが決まる。\(G(\alpha) \subset H\) の場合は前者になって \(\alpha\) の \(K’\) 上の最小多項式の次数は \(g_{\alpha}(x)\) の次数の \(\frac{1}{p}\) 倍になるから、\(K’\) 上では \(g_{\alpha}(x)\) は \(p\) 個の同次数の因子に既約分解して、\(\alpha\) の最小多項式に変化が起きる。一方 \(G(\alpha) \not\subset H\) で、\(G(\alpha)\) が \(H\) との共通部分をとることで真に縮小する場合は後者になり、体が \(K’\) になっても \(g_{\alpha}(x)\) は既約のままで \(K’\) 上の \(\alpha\) の最小多項式に変化はない。
前者の場合、\(M’=M\) 及びこの両辺に \(\beta\) を添加した \(L’ = L\) もなりたつから、\(M’\) 上の \(\beta\) の最小多項式は \(g_{\beta}(x)\) のまま、\(L’\) 上の \(\gamma\) の最小多項式も \(g_{\gamma}(x)\) のまま。
後者の場合、残る \(g_{\beta}(x)\), \(g_{\gamma}(x)\) のうちどちらが変化するのかわからないが、先ほどと同様の判定を続行できる。今度は、\(G(\alpha,\beta)\) が \(H\) との共通部分をとることによって真に縮小するかどうかを確かめる。\(H(\alpha,\beta) = H \cap G(\alpha,\beta)\) に対して、ふたたび第二準同型定理から
\[ G(\alpha,\beta) / (H \cap G(\alpha,\beta)) \cong (G(\alpha,\beta)H)/H \]
が \(G/H\) の部分群で単位群か \(p\) 次巡回群になるしかなく、\([L’:L]\) は \(1\) か \(p\) のどちらかになるしかない。それぞれに応じて、「\(g_{\beta}(x)\) の次数が \(\frac{1}{p}\) 倍に縮小して \(g_{\gamma}(x)\) はそのままになる」か、「\(g_{\beta}(x)\) は不変なままで必然的に \(g_{\gamma}(x)\) の次数が \(\frac{1}{p}\) 倍に縮小する」かのどちらになるが決まる、といった具合。
このようにして、最小多項式 \(g_{\alpha}(x)\), \(g_{\beta}(x)\), \(g_{\gamma}(x)\) のどれが更新されるかが決定できる。まとめると、次のようになる。
- \(G(\alpha), G(\alpha,\beta), \dotsc\) を求める。step2 以降なら、前 step での \(H(\alpha), H(\alpha,\beta), \dotsc\) がそっくりそのまま使えるので、改めて求める必要はない。
- \(H(\alpha) = H \cap G(\alpha), H(\alpha,\beta) = H\cap G(\alpha,\beta), \dotsc\) を求める。こうやって次々に \(H\) との共通部分を取っていくとき、変化しない最初の箇所を特定する。
- 変化する最後の \(G(\alpha,\dotsc)\) から変化しない最初の \(G(\alpha,\dotsc)\) に対応する体どうしの間に添加された解の最小多項式が、この step で更新される最小多項式になる。
続いて、特定できた最小多項式について、実際に新しい最小多項式を求める手順を述べる。ここでは、それが \(g_{\beta}(x)\) だったとしよう。この場合、\(H(\alpha)\) は \(G(\alpha)\) の真部分群だったが \(H(\alpha,\beta) = G(\alpha,\beta)\) で、\(L’=L\) となっている。そして \(g_{\beta}(x)\) は \(M’\) では \(p\) 個の因子 \(h_{1}(x), h_{2}(x), \dots, h_{p}(x)\) に分解し、その各々は \(H(\alpha)\) で不変になっている。第二準同型定理によって
\[ G(\alpha) / (H \cap G(\alpha)) \cong G/H \]
が \(p\) 次巡回群で、この同型を与える写像を通じて考えると、\(G(\alpha)-(H \cap G(\alpha))\) の元の任意のひとつ \(\sigma\) が \(G-H\) の元にもなっており、\(\sigma\) で決まるそれぞれの同値類が、それぞれの \(p\) 次巡回群の生成元となっている。\(h_{1}(x), h_{2}(x), \dots, h_{p}(x)\) の添字は \(\sigma\) で順次うつっていく順だとしてよい。
これらから、\(\theta_{1}(x), \dots, \theta_{p-1}(x), \theta_{p}(x)\) を作っておく。これまで通り、\(\zeta\) を \(1\) の原始 \(p\) 乗根として
\begin{align*}
\theta_{1}(x) &= h_{1}(x) + \zeta h_{2}(x) + \zeta^{2} h_{3}(x) + \dots + \zeta^{p-1} h_{p}(x) \\
\theta_{2}(x) &= h_{1}(x) + \zeta^{2}h_{2}(x) + (\zeta^{2})^{2} h_{3}(x) + \dots + (\zeta^{2})^{p-1} h_{p}(x) \\
&\vdots \\
\theta_{p-1}(x) &= h_{1}(x) + \zeta^{p-1} h_{2}(x) + (\zeta^{p-1})^{2} h_{3}(x) + \dots + (\zeta^{p-1})^{p-1} h_{p}(x) \\
\theta_{p}(x) &= h_{1}(x) + h_{2}(x) + \dots + h_{p}(x)
\end{align*}
とする。\(\theta_{p}(x)\) は \(\sigma\) で不変で、\(\theta_{i}(x) \; (i=1,\dots,p-1)\) は \(\sigma\) で \(\zeta^{-i}\) 倍になる。
上の例と同じように、\(K\) に添加して最小分解体が単拡大で作れるような原始元 \(u\) を見つける(上で注意した通り、\(\Q\) に対する原始元まで求める必要はない)。以前の記事と同じように、\(\alpha\), \(\beta\), \(\gamma\) の整数係数1次結合
\[ u = m_{1}\alpha + m_{2}\beta + m_{3}\gamma \]
で、\(G\) による作用ですべて異なる値になるようなものを見つければよい。そうすると、上と同じように \(\hat{h}_{1}(x), \dots, \hat{h}_{p}(x)\) が作れ、この添字は \(\sigma\) で順にうつっていく順番だとしてよい。
さらに、そこから \(\hat{\theta}(x)\) を作る。
\[ \hat{\theta}(x) = \hat{h}_{1}(x) + \zeta \hat{h}_{2}(x) + \zeta^{2} \hat{h}_{3}(x) + \dots + \zeta^{p-1} \hat{h}_{p}(x) \]
これは \(\sigma\) による作用で \(\zeta^{-1}\) 倍になる。したがって、\(\hat{\theta}(x)\) の最高次の係数を \(\hat{a}\) として
\begin{equation}
\label{eq:howto-new5-2}
\theta_{i}(x) = \hat{a}^{i} \eta_{i}(x) \quad (i=1,\dots,p-1)
\end{equation}
とおけば、\(\eta_{i}(x)\) は \(\sigma\) で不変である。この \(\eta_{i}(x)\) は、やはりただの係数比較だけで求まる。それを確認するために、現れる係数の範囲をちゃんと調べておこう。なお、簡単のため、「べき根の選び方の不定性によって \(0\) になる可能性もならない可能性もある式」は関わってこないものとする。
まず、\(h_{1}(x), \dots, h_{p}(x)\) の係数は \(H(\alpha)\) で不変だから \(M’\) の元で、したがって \(L’=L=K(\alpha,\beta)\) の元でもある。ということは、
\[ h_{1}(x) = (x-\beta)(x-\text{○}) \dotsm (x-\text{○}) \]
を展開した直後で求まる具体的な係数は \(K(\alpha,\beta,\gamma)\) の元の形をしているが、そこで \(g_{\gamma}(x)\), \(g_{\beta}(x)\), \(g_{\alpha}(x)\) を使って次数下げすれば \(\gamma\) は消え、\(K(\alpha,\beta)\) の元としての係数が具体的に求まるということだ。それを \(\sigma \in G(\alpha)\) で移していっても変わるのは \(\beta\) の部分だけだから、\(h_{2}(x), \dots, h_{p}(x)\) の係数はすべて \(K(\alpha,\beta)\) の元として具体的に求まる。同様に、\(\hat{h}_{1}(x), \dots, \hat{h}_{p}(x)\) の係数は \(H\) 不変だから \(K’\) の元で、従って \(L’=L=K(\alpha, \beta)\) の元でもある。よってこれも展開して次数下げすれば \(K(\alpha,\beta)\) の元としてすべて具体的に求まる。
すると \(\theta_{1}(x), \dots, \theta_{p-1}(x)\), \(\hat{\theta}(x)\) の係数と \(\hat{a}\) はすべて \(K(\alpha,\beta,\zeta)\) の元として具体的に求まる。よって\eqref{eq:howto-new5-2}で定まる \(\eta_{1}(x), \dots, \eta_{p-1}(x)\) の係数も \(K(\alpha,\beta,\zeta)\) の元だが、これらは特に \(H(\alpha)\) でも \(\sigma\) でも不変だから \(G(\alpha)\) でも不変。ということは実は \(K(\alpha,\zeta)\) の元になっている。
したがって、上の例の step2 でやっていたように、\eqref{eq:howto-new5-2}の両辺では実際には \(h_{i}(x)\) と \(\hat{a}^{i}\) を次数下げした後、\(\beta\) の多項式としての最高次の係数の比をとるだけで \(\eta_{i}(x)\) は求められる、ということがわかる。
ここまで来れば、後は上の例とまったく同様にして \(h_{1}(x)\)、つまり \(\beta\) の新しい最小多項式が \(M’\) 係数の多項式として求められる。
コメントを残す