$\newcommand{\pura}{(+)}
\newcommand{\mai}{(-)}
\newcommand{\Ai}{\mathrm{A_{1}}}
\newcommand{\Aj}{\mathrm{A_{3}}}
\newcommand{\Ak}{\mathrm{A_{5}}}
\renewcommand{\kumiawase}[2]{{}_{#1}\text{C}_{#2}}
\newcommand{\diag}{\operatorname{diag}}$
以下は、勤め先でけっこう以前に高校生の模試に出題された問題だ。（題意を変えない範囲で補足・修正した）

正六角形の各頂点を順に $\mathrm{A}_{1}$, $\mathrm{A}_{2}$, $\mathrm{A}_{3}$, $\mathrm{A}_{4}$, $\mathrm{A}_{5}$, $\mathrm{A}_{6}$ とする。動点 P は最初 $\mathrm{A}_{1}$ にいて、$1$ 秒ごとに隣の頂点に同じ確率で移動する。

$6$ 回の移動で初めて P が $\mathrm{A}_{1}$ に戻る確率 $p_{6}$ を求めよ。
正の整数 $k$ に対して、$2k$ 回の移動で初めて P が $\mathrm{A}_{1}$ に戻る確率 $p_{2k}$ を求めよ。
$n$ 回以内の移動で、初めて P が $\mathrm{A}_{1}$ に戻るまでの回数の平均値を $E_{n}$ とする。（$n$ 回以内に $\mathrm{A}_{1}$ に戻らない場合は $0$ 回と見なす）$E = \displaystyle\lim_{k \to \infty} E_{2k}$ を求めよ。

この問題は別に難しくはない。

【解】

対称性により、$p_{6}$ に含まれる「はじめに反時計回りに進んだ分の確率」と「はじめに時計回りに進んだ分の確率」は等しい。よって、前者を求めて $2$ 倍すればよい。

反時計回りの移動を$\pura$で表し、時計回りの移動を$\mai$で表すと、「最初が$\pura$で、6 回の移動で初めて P が $\Ai$ に戻る」ような移動は
$\pura\pura\pura\pura\pura\pura$
$\pura\pura\pura\mai\mai\mai$
$\pura\pura\mai\pura\mai\mai$
の $3$ 通りである。いずれの確率も $\Bigl( \dfrac{1}{2} \Bigr)^{6}$ずつであるから、
\[ \dfrac{p_{6}}{2} = 3 \times \Bigl( \dfrac{1}{2} \Bigr)^{6} \qquad \therefore p_{6} = \dfrac{3}{32} \]
まず、$p_{2}$ を求めてみる。適するのは「$\pura\mai$」「$\mai\pura$」のみで、$p_{2} = 2 \times \Bigl( \dfrac{1}{2} \Bigr)^{2} = \dfrac{1}{2}$ である。P は $\Ai$ から出発するので、偶数回の移動後の位置は $\Ai$, $\Aj$, $\Ak$ のいずれかしかありえないことに注意する。そこで、$2k$ 回の移動を $2$ 回ずつセットにしてまとめ、「$k$ 個のセット」と見ることにする。$p_{2k}$ は
1. はじめのセットで $\Aj$ か $\Ak$ に移り、
2. その後のセットではずっと $\Aj$ と $\Ak$ に留まったり行ったり来たりして、
3. 最後のセットで $\Ai$ に進む
ような確率である。

はじめのセットで $\Ai$ に留まる確率は $p_{2} = \dfrac{1}{2}$ である。対称性より、はじめのセットで $\Aj$ に移る確率と $\Ak$ に移る確率は等しく、それぞれ $\dfrac{1}{2}(1-p_{2}) = \dfrac{1}{4}$ ずつである。

これより、P がどの点から 1 セットで進む場合も、
- 元の点に留まる確率は $\dfrac{1}{2}$
- 反時計回りに 2 つ進んだ点に移る確率は $\dfrac{1}{4}$
- 時計回りに 2 つ進んだ点に移る確率も $\dfrac{1}{4}$
となる。したがって、P が $\Aj$, $\Ak$ にいる場合、どちらにいるかを問わず、1 つのセットで
- $\Ai$ に進む確率は $\dfrac{1}{4}$
- $\Ai$ に進まない（$\Aj$, $\Ak$ に留まるか移る）確率は $1-\dfrac{1}{4} = \dfrac{3}{4}$
である。

これより、
\[ p_{2k} = \Bigl( \underbrace{1- \dfrac{1}{2}}_{\text{(i)の分}} \Bigr) \times \underbrace{\Bigl( \dfrac{3}{4} \Bigr)^{k-2}}_{\text{(ii)の分}} \times \underbrace{\dfrac{1}{4}}_{\text{(iii)の分}} = \dfrac{1}{8} \Bigl( \dfrac{3}{4} \Bigr)^{k-2} \]
となる。ただし、(ii)の分は $k \geqq 2$ の場合しか存在しないので、まとめ
ると
\[ p_{2k} = \begin{cases}
\dfrac{1}{8} \Bigl( \dfrac{3}{4} \Bigr)^{k-2} & (\text{$k \geqq 2$ のとき}) \\
\dfrac{1}{2} & (\text{$k=1$ のとき})
\end{cases} \]
奇数回の移動で P が $\Ai$ に戻ることはありえない。よって、$2k$ 回以内の移動で初めて P が $\Ai$ に戻るのは
- $2$ 回目に初めて戻る
- $4$ 回目に初めて戻る
- $\vdots$
- $2k$ 回目に初めて戻る
のいずれかであるから、$E_{2k} = \displaystyle\sum_{l=1}^{k} 2l \times p_{2l}$ である。

よって、$k \geqq 2$ のとき
\[ E_{2k} = 2 \times p_{2} + \sum_{l=2}^{k} 2l \times \dfrac{1}{8} \Bigl( \dfrac{3}{4} \Bigr)^{l-2} = 1 + \dfrac{1}{4} \underline{\sum_{l=2}^{k}l \Bigl( \dfrac{3}{4} \Bigr)^{l-2}} \]
である。ここで、下線部を $S$ とおくと、$k \geqq 3$ のとき
\[\begin{array}{rrcll}
& S & = & 2 + & 3 \times \Bigl( \dfrac{3}{4} \Bigr) + 4 \times \Bigl( \dfrac{3}{4} \Bigr)^{2} + \dots + k \times \Bigl( \dfrac{3}{4} \Bigr)^{k-2} \\
-) & \dfrac{3}{4}S & = & & 2 \times \Bigl( \dfrac{3}{4} \Bigr) + 3 \times \Bigl( \dfrac{3}{4} \Bigr)^{2} + \dots + (k-1) \times \Bigl( \dfrac{3}{4} \Bigr)^{k-2} + k \times \Bigl( \dfrac{3}{4} \Bigr)^{k-1} \\
\hline
& \dfrac{1}{4} S & = & 2 + & \Bigl( \dfrac{3}{4} \Bigr) + \Bigl( \dfrac{3}{4} \Bigr)^{2} + \dots + \Bigl( \dfrac{3}{4} \Bigr)^{k-2} – k \times \Bigl( \dfrac{3}{4} \Bigr)^{k-1} \\
& & = & 2 + & \dfrac{3}{4} \times \dfrac{1-(3/4)^{k-2}}{1-(3/4)} – k \times \Bigl( \dfrac{3}{4} \Bigr)^{k-1} \\
& & = & 2 + & 3 \biggl( 1- \Bigl( \dfrac{3}{4} \Bigr)^{k-2} \biggr) – k \times \Bigl( \dfrac{3}{4} \Bigr)^{k-1}
\end{array} \]
である。これより
\[ E_{2k} = 1 + \dfrac{1}{4}S = 6 – 3\Bigl( \dfrac{3}{4} \Bigr)^{k-2} – k\Bigl( \dfrac{3}{4} \Bigr)^{k-1} \]
だから、$0 < \dfrac{3}{4} < 1$ に注意すれば
\[ E = \lim_{k \to \infty} E_{2k} = 6 \qquad \square \]

偶奇に着目すれば話が単純になって、高校生でも十分扱える問題になっている。

が、模範解答に書いてあった次のコメントが（私には）衝撃的だった。「実は、正六角形の代わりに正 $m$ 角形にしても、$E=m$ が成立します」

言うまでもなく、上の解は $m=6$ であることに強く依存したものになっている。偶奇性の議論は $m$ が奇数の場合はまったく通用しないし、$m$ が偶数であっても、$m>6$ になるともう「途中では $\Aj$ と $\Ak$ を行ったり来たりするだけ」という単純な話はなりたたなくなってくる。一体どうすれば $E=m$ なんてことが示せるんだ？

………という興味を惹かれてから数年。ここの所、以前見かけて気になっていた問題に、時間がある時に取り組んでみるということを続けていて、それがこの blog の主なネタ元になっているのだが、その一環としてこの問題に取りかかってみた。

実は、解ってしまえばこの問題は極端に難しいわけではなくスッキリ解決するし、ある有名問題にすぐ帰着もできるのだが、情けないことにそれにはまったく気づかず、とりあえずの解決に至るだけでも数週間がかりの悪戦苦闘になってしまった。ぶっ通しで考えていたわけではなくて、主に外出時の電車の中の時間つぶしとして飛び石的な時間の使い方しかしていなかったものの、それでも結構無様なことになってしまった。更にひどいことに、その時点では有名問題へ帰着可能であることに気づいておらず、こうやって blog 記事にまとめようと書きながら調査と考察を進める過程で次々と新事実（※私にとっての）が判明し、書き進める度に「しまったあ、そんな簡単なことにも気づいてなかったのかあああ！」と愕然として大幅書き直しを強いられる、という有様だった。

ここで考えた順に説明したりしたら、意味もなくあちこち寄り道する（そして袋小路にぶち当たる（笑））話になって読む側にとっては迷惑になるばかりだろうから、整理して「どうすればうまく行くか」という話を中心に進めていく。脱線は、必要最小限の話（以前「数学ガール」乱択アルゴリズム編を読んでいたときに個人的に引っかかった問題が、思いがけず解決できたという副産物）に留める。

■ 期待値の計算

以下では $m=7$ の場合を例にとって説明するが、$m$ が他の値の場合もまったく同様に解決する。いちいち $\Ai$ のように書くのが煩わしいので、頂点は単純に番号だけで表す。

$1$ から出発して、初めて $1$ に戻ってくるまでの回数の期待値を $E$ とする。また、$1$ から出発して、初めて $2$ に達するまでの回数の期待値を $F$ とする（途中で $1$ を通過することがあってもよい）。同様に、初めて $3$, $4$, …, $7$ に達するまでの回数の期待値を $G$, $H$, …, $K$ とする。

（対称性より明らかに $F=K$, $G=J$, $H=I$ だが、以下ではそれを明示的に使わない方がむしろやりやすい）

対称性から、例えば $6$ から出発して、初めて $1$ に達するまでの回数の期待値は $G$ と等しい。つまり、「どの点から出発する場合も、反時計回りに $2$ つ進んだ頂点に初めて到達するまでの回数の期待値は $G$ に等しい」わけだ。同様のことが他の値についてもなりたつ。

最初の 1 歩が $2$ に進むか $7$ に進むかで場合分けすると、$E$ を次のように表せる。
\begin{align}
E &= \underbrace{\frac{1}{2}}_{\text{$2$に進む確率}} \times (\underbrace{\underbrace{K}_{\text{$2$から初めて$1$に達するまでの平均回数}} + \underbrace{1}_{すでに1回動いた分}}_{\text{はじめに$2$に進んだときの期待値}}) \notag\\
&\quad + \underbrace{\frac{1}{2}}_{\text{$7$に進む確率}} \times (\underbrace{F+1}_{\text{はじめに$7$に進んだときの期待値}}) \notag\\
\label{eq:circular-randomwalk-1}
&= \frac{K+F}{2} + 1
\end{align}
$F$〜$K$ に対しても同様の立式を行うと
\begin{align}
\label{eq:circular-randomwalk-2}
F &= \frac{1}{2}\times 1 + \frac{1}{2}(G+1) = \frac{G}{2} + 1 \\
\label{eq:circular-randomwalk-3}
G &= \frac{1}{2}(F+1) + \frac{1}{2}(H+1) = \frac{F+H}{2} + 1 \\
\label{eq:circular-randomwalk-4}
H &= \frac{1}{2}(G+1) + \frac{1}{2}(I+1) = \frac{G+I}{2} + 1 \\
\label{eq:circular-randomwalk-5}
I &= \frac{1}{2}(H+1) + \frac{1}{2}(J+1) = \frac{H+J}{2} + 1 \\
\label{eq:circular-randomwalk-6}
J &= \frac{1}{2}(I+1) + \frac{1}{2}(K+1) = \frac{I+K}{2} + 1 \\
\label{eq:circular-randomwalk-7}
K &= \frac{1}{2}(J+1) + \frac{1}{2}\times 1 = \frac{J}{2} + 1
\end{align}
である。

\eqref{eq:circular-randomwalk-1}〜\eqref{eq:circular-randomwalk-7}を辺々足すと
\[ E+F+G+H+I+J+K = F+G+H+I+J+K + 7 \]
なので、両辺で $F$ から $K$ までが打ち消し合って $E = 7$ が得られる。
$\square$

ここでは期待値の無限級数としての収束性などはきちんと調べていないが、これだけでも本質は十分見てとれるだろう。実は本記事の最後に書くように無限性をいい加減にすますのは本当はまずいのだが、ここではこれ以上追及しないことにする。きちんと調べたい方はがんばっていただきたい。

なお「正 $m$ 角形」という仮定をそのまま受け取るなら $m \geqq 3$ ということになってしまうが、当然 $m=2$ の場合にも自然に拡張できて同じ $E=m$ という結果になる。

また、この結論は$\pura$回転と$\mai$回転の確率が等しくなくてもなりたつことがわかる。毎回確率が変わるようだとだめだが、$\pura$と$\mai$の確率がずっと一定のままなら、上の議論からすぐに $E=m$ が得られる。

■ 確率の漸化式

このように、期待値を主役にするとそれほど難しい問題でもなくすっきり解決するのだが、当初私は冒頭に掲げた元問題の解法に引きずられてしまい、確率を主役にしたため難航していた。それでも、私に十分な知識があれば十分解決可能な問題だったはずなのだが、後述するようにその知識を仕入れられたのが一連の考察の終盤になってからだったので、そこまではかなり迷走していた。

確率を主役にすると、こんな議論になる。やはり、$m=7$ の場合を例にとろう。

頂点 $1$ から出発して $n$ 回後までの間 $1$ に行くことなく、かつ $n$ 回後に $2$ にいる確率を $a_{n}$ とする。同様に、
\begin{align*}
b_{n} &= \text{「$n$ 回後までの間 $1$ に行くことなく、かつ $n$ 回後に $3$ にいる確率」} \\
c_{n} &= \text{「$n$ 回後までの間 $1$ に行くことなく、かつ $n$ 回後に $4$ にいる確率」} \\
d_{n} &= \text{「$n$ 回後までの間 $1$ に行くことなく、かつ $n$ 回後に $5$ にいる確率」} \\
e_{n} &= \text{「$n$ 回後までの間 $1$ に行くことなく、かつ $n$ 回後に $6$ にいる確率」} \\
f_{n} &= \text{「$n$ 回後までの間 $1$ に行くことなく、かつ $n$ 回後に $7$ にいる確率」}
\end{align*}
を定める。対称性により $a_{n}=f_{n}$, $b_{n}=e_{n}$, $c_{n}=d_{n}$ がただちにわかるので、以下必要に応じてこの関係も使っていく。

ちょうど $n$ 回で初めて 1 に戻る確率を $Q_{n}$ とすれば、
\[ Q_{n} = \begin{cases}
\underbrace{a_{n-1} \times \frac{1}{2}}_{\text{2から1に戻る}} + \underbrace{f_{n-1} \times \frac{1}{2}}_{\text{7から1に戻る}} = a_{n-1}
& (n \geqq 2) \\
0 & (n=1)
\end{cases} \]
であり、よって
\begin{equation}
\label{eq:circular-randomwalk-13}
E = \displaystyle\sum_{n=1}^{\infty} n Q_{n} = \sum_{n=2}^{\infty} n a_{n-1}
\end{equation}
である。ということは、素朴に考えれば $a_{n}$ の一般項が求められればいい。

確率の漸化式を自然に立式すると
\begin{align*}
a_{n+1} &= \underbrace{b_{n} \times \frac{1}{2}}_{\text{3から2へ}} = \frac{1}{2}b_{n} \\
b_{n+1} &= \underbrace{a_{n} \times \frac{1}{2}}_{\text{2から3へ}} + \underbrace{c_{n} \times \frac{1}{2}}_{\text{4から2へ}} = \frac{a_{n} + c_{n}}{2} \\
c_{n+1} &= b_{n} \times \frac{1}{2} + d_{n} \times \frac{1}{2} = \frac{b_{n} + d_{n}}{2}
\end{align*}
等がなりたち、行列を使って書くと、全体ではこんな式になる。
\begin{equation}
\label{eq:circular-randomwalk-17}
\begin{pmatrix}
a_{n+1} \\ b_{n+1} \\ c_{n+1} \\ d_{n+1} \\ e_{n+1} \\ f_{n+1}
\end{pmatrix} = \begin{pmatrix}
0 & \frac{1}{2} & 0 & 0 & 0 & 0 \\
\frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 & 0 \\
0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 \\
0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\
0 & 0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} \\
0 & 0 & 0 & 0 & \frac{1}{2} & 0
\end{pmatrix}
\begin{pmatrix}
a_{n} \\ b_{n} \\ c_{n} \\ d_{n} \\ e_{n} \\ f_{n}
\end{pmatrix}
\end{equation}
これと初期条件
\begin{equation}
\label{eq:circular-randomwalk-11}
a_{1} = f_{1} = \frac{1}{2}, \quad b_{1}=c_{1}=d_{1}=e_{1}=0
\end{equation}
から各数列が定まる。

一般の $m$ の場合は、\eqref{eq:circular-randomwalk-17}右辺の係数行列は対角線の上下に $\frac{1}{2}$ がズラッと並ぶ
\[ A = \begin{pmatrix}
& \frac{1}{2} &&&&& \\
\frac{1}{2} & & \frac{1}{2} &&&& \\
& \frac{1}{2} & & \frac{1}{2} &&& \\
&& \ddots & & \ddots & \\
&&& \ddots & \ddots \\
&&&& \frac{1}{2} & & \frac{1}{2} \\
&&&&& \frac{1}{2}
\end{pmatrix} \]
の形となる。

無知な私は、当初この行列の $n$ 乗は求まらないだろう、と見切りをつけて別の方針でいろいろ考えていたのだが、その愚かさを打ち砕いてくれたのが「高校数学の美しい物語」三重対角行列の特殊形の固有値は綺麗だった。恥ずかしながら、「三重対角行列」という名称や、それについてのこの性質は今回初めて知った。【2018, 7/16 追記】と思ったら、しばらく前に、学部時代のノートを色々見返す機会があったのだが、実はなんとその中に $2A$（$1$ がズラッと並ぶ形の行列）の固有値・固有ベクトルが書いてあった！何の導出もなくいきなり結果だけが書いてあったのはおそらくその授業が「数値計算」の科目だったからなのだろう。全然覚えてなかった…。試験なしのレポートで成績をつける科目だったので、当時はノートをきちんと復習する機会のなかった科目だったのだろう（とは言っても、仮に試験ありだったとしても、ここまで特殊な知識を、当時の私が記憶に値する事項だと思うとは思えないので、仮に試験対策で一時的に覚えたことはあったとしても、それはすぐ忘れ去っていただろうことはほぼ間違いない）。

この記事はまさしくそのものズバリで、$A$ はそこで言う $T\bigl(0,\frac{1}{2}\bigr)$ であり、そこで書かれているように固有ベクトル
\begin{equation}
\label{eq:circular-randomwalk-8}
\vec{x}_{i} = \begin{pmatrix}
\sin \Bigl( \frac{i\pi}{m} \Bigr) \\
\sin \Bigl( \frac{2i\pi}{m} \Bigr) \\
\vdots \\
\sin \Bigl( \frac{(m-1)i\pi}{m} \Bigr)
\end{pmatrix}
\end{equation}
及び固有値
\begin{equation}
\label{eq:circular-randomwalk-9}
\lambda_{i} = \cos \Bigl( \frac{i\pi}{m} \Bigr)
\end{equation}
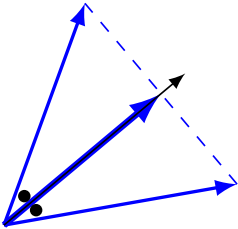
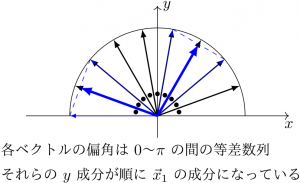
を持っている（$i=1,2,\dots,m-1$）。これは要するに、「偏角が等差数列になっている単位ベクトルの列があるとき、1 つおきに足して $2$ で割ったベクトルは 2 等分線の方向を向き、挟まれている中央のベクトルと重なる。その倍率は $\cos$ で表せる」という当たり前のことが背景だ。

それを、$0$ で始まり $\pi$ の整数倍で終わる等差数列の偏角に対して使うとこうやって $A$ の固有ベクトルと固有値になる、というわけで、どこにも難しい所はない。例えば、次の図は $\vec{x}_{1}$ の成分がどう得られるかを図解したものだ。各ベクトルの偏角を $2$ 倍、$3$ 倍、…とすると $\vec{x}_{2}$, $\vec{x}_{3}$,… の図になる。

\eqref{eq:circular-randomwalk-8}, \eqref{eq:circular-randomwalk-9}が自力で出てこなかった言い訳: 一応、「$A$ は結構きれいな形の行列だから、学部時代の線形代数の教科書等にこんな形の行列の固有値・固有ベクトルを求める例題でも載ってないかな？」ということは探してみたのですが、見つかりませんでした。もっとたくさん買い揃えておくべきでしたね、学部時代の私よ…。似た形の「巡回行列」には目は止まったのですが、（当然ながら）「逆の端から顔を出してる成分がないから巡回行列にはなってないなあ…」ということで、役に立たないと判断して見送りました（結果が解った今となってはやはり「いくら形が似ているとは言え、その微小な違いが今回はやはり効いていて、巡回行列の知識はこの $A$ の $n$ 乗を考える上では役に立たない」とはっきり解るので、見送った判断が正しかったことも解ります）。また、既存の文献に頼るばかりでなく、自分でも「$\det(xI-A)$ が綺麗に求まったりしないだろうか」ということは軽く計算しかかったことはあったのですが、その時はこれが $\cos$ を使って厳密根が表せる多項式（Chebyshev 多項式をちょっと加工したものになりますね）になっている、ということは、恥ずかしながら見抜くに至りませんでした。

では、これを使っても期待値が求められることを計算で確認してみよう。\eqref{eq:circular-randomwalk-9}の $m-1$ 個の固有値は互いに異なるから、\eqref{eq:circular-randomwalk-8}の固有ベクトルは $\mathbb{R}^{m-1}$ の基底になっていて、そのまま $n$ 乗計算に使える。
\[ A( \vec{x}_{1}, \vec{x}_{2}, \dots, \vec{x}_{m-1}) = ( \vec{x}_{1},
\vec{x}_{2}, \dots, \vec{x}_{m-1})
\begin{pmatrix}
\cos\Bigl( \frac{\pi}{m} \Bigr) & 0 & 0 & \dots & 0 \\
0 & \cos\Bigl( \frac{2\pi}{m} \Bigr) & 0 & \dots & 0 \\
& & \ddots & & \\
0 & 0 & 0 & 0 & \cos \Bigl( \frac{(m-1)\pi}{m} \Bigr)
\end{pmatrix} \]
より、$P = ( \vec{x}_{1}, \vec{x}_{2}, \dots, \vec{x}_{m-1})$ とおけば
\begin{align}
A P &= P \diag\biggl( \cos\Bigl( \frac{\pi}{m} \Bigr), \cos\Bigl( \frac{2\pi}{m} \Bigr), \dots, \cos \Bigl( \frac{(m-1)\pi}{m} \Bigr) \biggr) \notag\\
\label{eq:circular-randomwalk-10}
\therefore A^{n} P &= P \diag\biggl( \cos^{n}\Bigl( \frac{\pi}{m} \Bigr), \cos^{n}\Bigl( \frac{2\pi}{m} \Bigr), \dots, \cos^{n}\Bigl( \frac{(m-1)\pi}{m} \Bigr) \biggr)
\end{align}
である。

ここから $a_{n}$ や $Q_{n}$ 等を求めたいと思っているわけだが、\eqref{eq:circular-randomwalk-17}, \eqref{eq:circular-randomwalk-11}から
\[
\begin{pmatrix}
a_{n} \\ b_{n} \\ \vdots \\ f_{n}
\end{pmatrix}
= A^{n-1}
\begin{pmatrix}
a_{1} \\ b_{1} \\ \vdots \\ f_{1}
\end{pmatrix}
= A^{n-1} \cdot \frac{1}{2}
\begin{pmatrix}
1 \\ 0 \\ \vdots \\ 0 \\ 1
\end{pmatrix}
\]
なので、\eqref{eq:circular-randomwalk-10}をそのまま使おうとすると $P^{-1}$ を計算させられることになる。これはできれば避けたい計算なので、いきなり直接的な計算にとりかかる前に、もうちょっとラクができないか検討してみることにする。

まず $A$ は実対称行列だから、その固有ベクトルは直交系をなすように取れる。さらに、今は固有値がすべて異なるので、異なる $\vec{x}_i$ 同士はすべて直交する。これは $^{T}PP$ が対角行列になることを意味するから、$P^{-1}$ は $^{T}P$ と大体同じで、後者を必要に応じてちょっと加工するだけで得られる、というわけだ。さらに $P$ 自身も実は対称行列（なぜならば、$P$ の $i,j$ 成分は $\sin \bigl( \frac{ij \pi}{m} \bigr)$ で $i$, $j$ について対称）だから、結局 $P^{2}$ が対角行列になって、$P^{-1}$ は $P$ と大差ない、ということになる。対角行列 $P^{2}$ の対角成分とは $\lvert \vec{x}_{i} \rvert^{2}$ にほかならない。計算してみよう。
\begin{align}
\lvert \vec{x}_{i} \rvert^{2} &= \sin^{2}\Bigl(\frac{i\pi}{m} \Bigr) +
\sin^{2}\Bigl( \frac{2i\pi}{m}\Bigr) + \dots + \sin^{2}\Bigl( \frac{(m-1)i\pi}{m} \Bigr) \notag\\
&= \frac{1-\cos( 2i\pi/m )}{2} + \frac{1-\cos(4i\pi/m)}{2} + \dots + \frac{1-\cos(2(m-1)i\pi/m)}{2} \notag\\
\label{eq:circular-randomwalk-12}
&= \frac{1}{2}\biggl(m-1 – \Bigl( \underline{\cos \frac{2i\pi}{m} + \cos \frac{4i\pi}{m} + \dots + \cos \frac{2(m-1)i\pi}{m}} \Bigr) \biggr)
\end{align}
この下線部はすぐに $-1$ とわかる（なぜならば: まず、単位円周を $m$ 等分するベクトルの和は対称性から $\vec{0}$ になるが、その $m$ 本のベクトルのうち $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$ を除いた $m-1$ 本の和の $x$ 成分が $i=1$ の時の下線部に等しいから、$i=1$ の場合は OK。$i>1$ の場合も同様に示せる）。よって
\[ \eqref{eq:circular-randomwalk-12} = \frac{1}{2}(m-1-(-1)) = \frac{m}{2} \]
となる。これが $i$ によらない定数なので、結局 $P^{2}$ は
\begin{equation}
\label{eq:circular-randomwalk-14}
P^{2} = \frac{m}{2} I
\end{equation}
となり、$P^{-1}=\frac{2}{m}P$ とわかる。ここまで単純化されれば、もはや $P^{-1}$ という形を表に出さなくてもいい。

\eqref{eq:circular-randomwalk-10}の両辺に右から $P$ をかければ、\eqref{eq:circular-randomwalk-14}によって
\begin{equation}
\label{eq:circular-randomwalk-15}
\frac{m}{2} A^{n} = P \diag\biggl( \cos^{n}\Bigl( \frac{\pi}{m} \Bigr),
\cos^{n}\Bigl( \frac{2\pi}{m} \Bigr), \dots, \cos^{n}\Bigl(
\frac{(m-1)\pi}{m} \Bigr) \biggr) P
\end{equation}
が得られる。

さらに、$Q_{n}$ の導出を見れば、$Q_{n}$ に等しいのは $a_{n-1}$ と言うよりむしろ $\frac{a_{n-1}+f_{n-1}}{2}$ だ。そこで、次のものを計算すればいい。
\begin{align}
\frac{a_{n}+f_{n}}{2} &= \frac{1}{2} (1, 0, \dots, 0, 1)
\begin{pmatrix}
a_{n} \\ b_{n} \\ \vdots \\ f_{n}
\end{pmatrix} \notag\\
\label{eq:circular-randomwalk-16}
&= \frac{1}{2} (1, 0, \dots, 0, 1) A^{n-1} \cdot \frac{1}{2}
\begin{pmatrix}
1 \\ 0 \\ \vdots \\ 0 \\ 1
\end{pmatrix}
\end{align}
これは $A^{n-1}$ の両側を $\frac{1}{2} \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 1 \end{pmatrix}$ で挟んだものだ。よって\eqref{eq:circular-randomwalk-15}から、
$\diag\biggl( \cos^{n}\Bigl( \frac{\pi}{m} \Bigr), \cos^{n}\Bigl( \frac{2\pi}{m} \Bigr), \dots, \cos^{n}\Bigl( \frac{(m-1)\pi}{m} \Bigr) \biggr) (=D(n) \text{ とおく})$ を $\frac{1}{2}P \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 1 \end{pmatrix}$ で挟んだものが求まればよい。

ここで
\[ \frac{1}{2}P \begin{pmatrix}
1 \\ 0 \\ \vdots \\ 1
\end{pmatrix} = \frac{1}{2} (\vec{x}_{1} + \vec{x}_{m-1}) \]
の第 $j$ 成分は
\[ \frac{1}{2} \Bigl( \sin \frac{j\pi}{m} + \sin \frac{(m-1)j\pi}{m} \Bigr) = \begin{cases}
0 & \text{($j$ が偶数のとき)} \\
\sin \frac{j\pi}{m} & \text{($j$ が奇数のとき)}
\end{cases} \]
であるから、$D(n)$ を $\frac{1}{2}P \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 1 \end{pmatrix}$ で挟んだものはこうなる。
\begin{equation}
\label{eq:circular-randomwalk-17-2}
\Bigl( \sin \frac{\pi}{m}, 0 , \sin \frac{3\pi}{m}, 0, \dots \Bigr) D(n)
\begin{pmatrix}
\sin \frac{\pi}{m} \\ 0 \\ \sin \frac{3\pi}{m} \\ 0 \\ \vdots
\end{pmatrix} = \sin^{2} \frac{\pi}{m} \cos^{n} \frac{\pi}{m} + \sin^{2} \frac{3\pi}{m} \cos^{n} \frac{3\pi}{m} + \dotsb
\end{equation}

よって、\eqref{eq:circular-randomwalk-15}で $n$ を $n-1$ に置きかえてから両辺を $\frac{1}{2} \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 1 \end{pmatrix}$ で挟めば、\eqref{eq:circular-randomwalk-16}によって
\begin{align*}
\frac{m}{2} \cdot \frac{a_{n}+d_{n}}{2} &= \text{《\eqref{eq:circular-randomwalk-17-2}右辺で$n$を$n-1$で置きかえたもの》} \\
\therefore \frac{m}{2} Q_{n} = \frac{m}{2} \cdot \frac{a_{n-1}+d_{n-1}}{2} &= \text{《\eqref{eq:circular-randomwalk-17-2}右辺で$n$を$n-2$で置きかえたもの》} \\
&= \sin^{2} \frac{\pi}{m} \cos^{n-2} \frac{\pi}{m} + \sin^{2} \frac{3\pi}{m} \cos^{n-2} \frac{3\pi}{m} + \dots \quad (n\geqq 2) \\
\therefore \frac{m}{2} E = \frac{m}{2} \sum_{n=1}^{\infty} nQ_{n} &=
\sin^{2} \frac{\pi}{m} \sum_{n=2}^{\infty} n \cos^{n-2} \frac{\pi}{m} + \sin^{2} \frac{3\pi}{m} \sum_{n=2}^{\infty} n\cos^{n-2} \frac{3\pi}{m} + \dotsb
\end{align*}
となる。ここで、$\lvert \lambda \rvert < 1$ のとき
\[ S(\lambda) = \sum_{n=2}^{\infty} n \lambda^{n-2} = \frac{2-\lambda}{(1-\lambda)^{2}} \]
（導出過程は省略）となることから
\begin{equation}
\label{eq:circular-randomwalk-30}
\frac{m}{2} E = \sin^{2} \frac{\pi}{m} S\Bigl(\cos \frac{\pi}{m}\Bigr) + \sin^{2} \frac{3\pi}{m} S\Bigl( \cos \frac{3\pi}{m} \Bigr) + \dots
\end{equation}
となって、この和が計算できれば期待値 $E$ が求められることになる。

\eqref{eq:circular-randomwalk-30}右辺は次の形の項の和だ。
\begin{equation}
\label{eq:circular-randomwalk-31}
\sin^{2} \frac{j\pi}{m} S\Bigl(\cos \frac{j\pi}{m}\Bigr) = \sin^{2} \frac{j\pi}{m}\times \frac{2-\cos (j\pi/m)}{\bigl(1-\cos(j\pi/m)\bigr)^{2}} \quad \text{($j$は$m-1$以下の正の奇数)}
\end{equation}
ここでちょっといやなのが、和の項数が $m$ の偶奇に左右されてしまうことだ。前節の考察から、最終的には $E=m$ という綺麗な形になるはずなので、何とかうまい処理で偶奇の場合分けが回避できないか…と思って式を眺めてみると、\eqref{eq:circular-randomwalk-30}左辺に $\frac{m}{2}$ がついているので、$E$ を求めるときには最終的に「$2$ 倍して $m$ で割る」という計算をすることになる。この「$2$ 倍する」という所からすると、ひとつの仮説として「\eqref{eq:circular-randomwalk-30}の右辺は、実は同じものをダブらせて足したものが言わば『本来の姿』なのではないか？」という点がちょっと臭い。

ダメもとでこの仮説を試してみよう。まず\eqref{eq:circular-randomwalk-31}の右辺を $\theta = j\pi/m$ とおいて整理すると、次のように $\cos$ だけを使った形にできる。
\begin{align}
\sin^{2} \theta \frac{2-\cos \theta}{(1 – \cos \theta)^{2}} &= (1- \cos^{2} \theta) \frac{2 – \cos \theta}{(1 – \cos \theta)^{2}} \notag\\
\label{eq:circular-randomwalk-32}
&= \frac{(1 + \cos \theta ) ( 2 – \cos \theta)}{1 – \cos \theta}
\end{align}
\eqref{eq:circular-randomwalk-30}では $j$ を「$m$ 未満の正の奇数」の範囲で足していた。このとき $\cos$ の偏角 $\theta = j\pi/m$ は単位円の上半分に分布していたが、試しに $j$ の範囲を「$2m$ 未満の正の奇数」にしてみよう。つまり $j=1,3,5,\dots,2m-1$ とするわけである。すると $\theta$ は単位円に上下対称に分布するので、基本的に和が $2$ 倍になったことになる。

気をつけなければいけないのは、こうやって和の範囲を広げると、図のように偏角がちょうど $\pi$ になるときの項も余分に足してしまうことだが、うまいことに $\theta=\pi$ のときは\eqref{eq:circular-randomwalk-32}は $0$ になるので和に影響しない。したがって、 $j$ の範囲を「$2m$ 未満の正の奇数」にすることで、和の値はちょうど $2$ 倍になるとわかった（※ $\theta$ がちょうど $\pi$ になることがあるのは $m$ が奇数のときだが、上のように議論すれば $m$ の偶奇は特に気にしなくてもうまく行く）。

今の考察と\eqref{eq:circular-randomwalk-30}から、
\begin{align}
mE &= 2 \sum_{j:\text{$m$未満の正の奇数}} \frac{\bigl(1 + \cos(j\pi/m)\bigr) \bigl( 2 – \cos(j\pi/m)\bigr)}{1 – \cos(j\pi/m)} \notag\\
\label{eq:circular-randomwalk-33}
&= \sum_{j:\text{$2m$未満の正の奇数}} \frac{\bigl(1 + \cos(j\pi/m)\bigr) \bigl( 2 – \cos(j\pi/m)\bigr)}{1 – \cos(j\pi/m)}
\end{align}
で、後は\eqref{eq:circular-randomwalk-33}が計算できればいい。
\begin{align*}
\frac{(1 + \cos\theta ) ( 2 – \cos\theta)}{1 – \cos\theta} &= \frac{2 + \cos\theta – \cos^{2}\theta}{1 – \cos\theta} \\
&= \cos\theta + \frac{2}{1 – \cos\theta}
\end{align*}
であるから
\[ \eqref{eq:circular-randomwalk-33} = \sum_{j:\text{$2m$未満の正の奇数}} \cos \frac{j\pi}{m} + \sum_{j:\text{$2m$未満の正の奇数}} \frac{2}{1 – \cos(j\pi/m)} \]
だが、１つ目の和は単位円を $m$ 等分するベクトルの和の $x$ 成分なので直接 $0$ とわかる。したがって、結局
\begin{equation}
\label{eq:circular-randomwalk-35}
mE = \sum_{j=1,3,5,\dots,2m-1} \frac{2}{1 – \cos (j\pi/m)}
\end{equation}
という所まで整理できた。

$E=m$ になるはずだから、\eqref{eq:circular-randomwalk-35}の右辺は $m^{2}$ になるはずで、実際小さな自然数を代入してみると確かに $m^{2}$ になる（元々の問題設定から、暗黙のうちに $m \geqq 2$ のはずだが、この式の形なら $m=1$ の場合も含めて成立している）。割と綺麗な形の式なので、きっと簡潔で巧妙な式変形があるのだろうが、自力では思いつけなかったので、以下のように複素数表示にモノを言わせて強引に片付けてしまった。

まず、$z=e^{i\theta}$ とおくと $\cos\theta = \frac{1}{2} \Bigl( z + \frac{1}{z} \Bigr)$ だから、
\begin{align}
\frac{2}{1-\cos\theta} &= \frac{2}{1-\frac{1}{2}\bigl( z + \frac{1}{z} \bigr)} \notag\\
\label{eq:circular-randomwalk-34}
&= \frac{4z}{2z-(z^{2}+1)} = -\frac{4z}{(z-1)^{2}}
\end{align}
したがって、$\alpha=e^{\frac{\pi}{m}i}$ とおくと、\eqref{eq:circular-randomwalk-35}は\eqref{eq:circular-randomwalk-34}に $z=\alpha, \alpha^{3}, \dots, \alpha^{2m-1}$ を代入して和を取ったもの。これら $m$ 個の値は、$x^{m}=-1$ の異なる $m$ 個の複素数解である。$z$ がこの $m$ 個のどれであっても、以下の式がなりたつ。
\begin{align}
0 &= z^{m}+1 = z^{m}-1 + 2 \notag\\
&= (z-1)(z^{m-1}+z^{m-2}+ \dots + z + 1) + 2 \notag\\
\therefore – \frac{2}{z-1} &= z^{m-1}+z^{m-2}+ \dots + z + 1 = \sum_{k=0}^{m-1} z^{k} \label{181734_17Sep17}\\
z^{k} &= z^{k}-1 + 1 \notag\\
&= (z-1)(\underbrace{z^{k-1}+ \dots + 1}_{\text{$k=0$のときは$0$}}) + 1 \notag\\
\therefore \frac{z^{k}}{z-1} &= \underbrace{z^{k-1} + \dots + 1}_{\text{$k=0$のときは$0$}} + \frac{1}{z-1} \notag\\
\therefore -\frac{2}{(z-1)^{2}} &= \sum_{k=0}^{m-1} \frac{z^{k}}{z-1} \notag\\
&= \sum_{k=0}^{m-1} \Bigl( \underbrace{z^{k-1} + \dots + 1}_{\text{$k=0$のときは$0$}} + \frac{1}{z-1} \Bigr) \notag\\
&= \sum_{k=0}^{m-1} (\underbrace{z^{k-1} + \dots + 1}_{\text{$k=0$のときは$0$}}) + \frac{m}{z-1} \notag\\
&= \sum_{k=1}^{m-1} (z^{k-1} + \dots + 1) – \frac{m}{2}(z^{m-1} + \dots + 1) \notag\\
\label{eq:circular-randomwalk-37}
\therefore -\frac{4z}{(z-1)^{2}} &= 2\sum_{k=1}^{m-1} (z^{k} + \dots + z) – m (\underbrace{z^{m}}_{-1} + \dots + z)
\end{align}
これに $z=\alpha, \alpha^{3}, \alpha^{5}, \dots, \alpha^{2m-1}$ を代入して和を取ったものが $mE$ である。ここで、\eqref{eq:circular-randomwalk-37}の右辺は $z^{l}$ の形の項ばかりが現れており、かつその大半が $1 \leqq l \leqq m-1$ であることに注意する。この $z^{l}$ に対し $z=\alpha, \alpha^{3}, \alpha^{5}, \dots, \alpha^{2m-1}$ を代入した和をとると
\begin{equation}
\label{eq:circular-randomwalk-36}
\alpha^{l} + \alpha^{3l} + \alpha^{5l} + \dots + \alpha^{(2m-1)l}
\end{equation}
という等比数列の和であり、その公比は $\alpha^{2l}= e^{\frac{2l\pi}{m}i} \ne 1 \quad (\because 1 \leqq l \leqq m-1)$ であるから
\begin{align*}
\eqref{eq:circular-randomwalk-36} &= \alpha^{l} \times \frac{\alpha^{2ml}-1}{\alpha^{2l}-1} \\
&= \alpha^{l} \times \frac{(-1)^{2l}-1}{\alpha^{2l}-1} = 0
\end{align*}
となって消える。よって残る値は $z^{l} \quad (1\leqq l \leqq m-1)$ の形をしていない $(-m)(-1)=m$ の和のみであり、
\[ mE = \underbrace{m + m + \dots + m}_{\text{$m$個}} = m^{2} \]
で、これにより $E=m$ が示された。

【 2017/11/12 追記】
\eqref{181734_17Sep17}の後の変形はこうした方が気が利いてますね。
\begin{align}
\therefore \Bigl(- \frac{2}{z-1} \Bigr)^{2} &= (z^{m-1}+ z^{m-2} + \dots + z + 1)^{2} \notag\\
\therefore \frac{4}{(z-1)^{2}} &= z^{m-1}(1 + z^{-1} + \dots + z^{-(m-1)}) (z^{m-1}+ z^{m-2} + \dots+ z + 1) \notag\\
\therefore -\frac{4z}{(z-1)^{2}} &= -\underbrace{z^{m}}_{-1} (1 + z^{-1} + \dots + z^{-(m-1)}) (1 + z + \dots + z^{m-1}) \notag\\
&= \underbrace{1 + z^{-1+1} + z^{-2+2} + \dots + z^{-(m-1)+m-1}}_{m} + \sum_{j \ne k} z^{-j+k}\label{022901_17Sep17}
\end{align}
これに $z=\alpha, \alpha^{3}, \alpha^{5}, \dots, \alpha^{2m-1}$ を代入して和を取ったものが\eqref{eq:circular-randomwalk-35}である。ここで、\eqref{022901_17Sep17}の $\sum$ 記号の部分に現れる $-j+k$ を $l$ とおくと、$0 \leqq j, k \leqq m-1$ かつ $j \ne k$ により $1 \leqq \lvert l \rvert \leqq m-1$ である。この $z^{l}$ に対し $z=\alpha, \alpha^{3}, \alpha^{5}, \dots, \alpha^{2m-1}$ を代入した和をとると
\begin{equation}
\label{eq:circular-randomwalk-36-2}
\alpha^{l} + \alpha^{3l} + \alpha^{5l} + \dots + \alpha^{(2m-1)l}
\end{equation}
という等比数列の和であり、その公比は $\alpha^{2l}= e^{\frac{2l\pi}{m}i} \ne 1 \quad (\because 1 \leqq \lvert l \rvert\leqq m-1)$ であるから
\begin{align*}
\eqref{eq:circular-randomwalk-36-2} &= \alpha^{l} \times \frac{\alpha^{2ml}-1}{\alpha^{2l}-1} \\
&= \alpha^{l} \times \frac{(-1)^{2l}-1}{\alpha^{2l}-1} = 0
\end{align*}
となって消える。よって残る値は
\[ \eqref{eq:circular-randomwalk-35} = \underbrace{m + m + \dots + m}_{\text{$m$個}} = m^{2} \square \]

ここでは「$E=m$ になるはず」という見通しがあったから\eqref{eq:circular-randomwalk-35}に対してここまで長々とした式変形を粘り強くやり遂げる意思が沸いてきたが、もしそうでなかったら、もっと手前で「この式は綺麗に変形できるものではないだろう」と放棄してしまっていたかもしれない。

■ 有名問題への帰着

さて、上で述べた通り、当初私は $A$ の固有値・固有ベクトルが厳密に求まるとは思っていなかったため、別のアプローチを色々と考えていた。そのとき得られた着想のひとつは、こういうものだった: 最初の $1$ 歩は頂点 $2$ に出るか $m$ に出るかのどちらかしかないが、その後のなりゆきは対称性によって事実上同じ（左右反転しただけ）だから、$2$ に出た後のことが解析できれば十分。さらに「初めて」$1$ に戻るまでのことを考えるので、途中は一切 $1$ に行かないから、結局頂点が環状に並んでいることを考慮する必要はなくて、頂点 $1$ で切り開いてまっすぐ並べ直しても同じことになる。

つまり、$1$ 次元での有限の長さの鎖上で考えたランダムウォークと同じ。両端の頂点 $1$ のどちらかに着いたら終了だから、何のことはない、これは有名な「破産の確率」（ギャンブラー破産問題）そのものである。

そんなことはとっくに気づいていた、という方も多いだろう。それどころか、「それ以外の見方なんか、最初から思いつきもしなかった」という方もたくさんいらっしゃるのではないだろうか（というか、さらに言えばこの「円環型ランダムウォーク」という題材は、ひょっとしたら確率過程をやってらっしゃる方からすれば常識的な有名問題で、本記事のここまでの話もここ以降の話も何の新規性もないつまらない話ではないかと懸念している）。しかしともかく、この問題に取り組んでいたしばらく前の私にとっては、この当たり前の視点さえ「新鮮な発見」であった。なので以下しばらくこの話を続けるが、興味のない方は次の節まで飛ばして頂きたい。

話を戻そう。当初この問題を考えているときに、参考となりそうな資料を web 検索していた時は芳しい成果が上がらなかったのだが、それはその時はまだ適切なキーワードに至っていなかったからだった。こうやって単なる「$1$ 次元有限格子上のランダムウォーク」「破産の確率」であると気づいてしまえば、たちまちのうちにほとんどそのままズバリ答が書いてある資料を見つけ出すことができた。
確率論 II – ランダム・ウォーク
これの最後の方の「9 破産問題」「10 破産問題 – いつ決着がつくか」に詳しい解析がある。導出もちゃんと書いてあるので、ここでは結果を引用するだけにする（この節だけで閉じているので、1〜8節を事前に読んでおく必要はないようだ）。

そこでの、所持金 $0$ の状態（破産）および所持金 $a$ の状態（上がり）が本記事の頂点 $1$ に対応し、10節での $D(n)$（所持金 $n$ の状態から始めて賭けの決着が着くまでの回数の期待値）が、本記事の上の方で出てきた期待値 $F, G, \dotsc$ に対応している。よって $a=m$, $p=q=\frac{1}{2}$ としたときの $D(1)$ が本記事での $K$ で、
\[ K = D(1) = 1(a-1) = m-1 \quad \therefore E= \frac{F+K}{2}+1 = K+1 = m \]
となって $E=m$ が再現できた。（また、$D(n)=n(a-n)$ の式から $G, H, \dotsc$ なども容易にわかる。もちろんこれは\eqref{eq:circular-randomwalk-1}〜\eqref{eq:circular-randomwalk-7}からもすぐ得られるが、そうやって出した値の背景がこの $D(n)$ の式一発でわかってしまうという所が優れている）

また、そこでの $u(z,n)$ や $v(z,n)$ がこちらでの $a_{n}$ 等と関連している（なぜか当該文書内での文字の使い方が一貫していなくて、$u(z,n)$ や $v(z,n)$ では $D(n)$ と違って $n$ は「始めの所持金」ではなく「終了までの回数」であり、始めの所持金は $z$ で表されているのがちょっとわかりにくい）。
\begin{align*}
u(z,n) &= \text{「所持金$z$の状態から始めて、$n$回後に初めて所持金$0$になる確率」} \\
v(z,n) &= \text{「所持金$z$の状態から始めて、$n$回後に初めて所持金$a$になる確率」}
\end{align*}
なので、$a=m$, $p=q=\frac{1}{2}$ とすると本文書での確率は
\begin{align*}
a_{n} &= \text{「$1$から出発して、$n$歩後までに$1$を通ることなく、$n$歩進んだ後に$2$にいる確率」} \\
&= \text{「$2$から出発して、$n$歩後までに$1$を通ることなく、$n$歩進んだ後に$1$にいる確率」} \\
&= \text{「所持金$1$から出発して、$n$回後に初めて所持金が$0$か$a$になる確率」} \\
&= u(1,n) + v(1,n)
\end{align*}
となる（２つ目の等号がなりたつ理由は、動きを時間反転してみればわかる）。するとこの確率は、当該文書中の母関数 $U(z,s)$, $V(z,s)$ を使って表せるはずだ。そこで、当該文書での typo 的なミスを修正した上で、$a_{n}$ の一般項の表式を出しておこう。

当該文書 (10.3) 式は、$n=1$ の場合も含めて成立する（立式段階では安全のため $n \geqq 2$ から出発してもいいのだが、どこかの段階でこれを確かめておかないと、後の方で $U(z,s)$ の漸化式を導くときの変形ができない）。
「母関数の性質」枠内中 (iv) は $U$ の $k$ 階微分の式からプライム取り忘れ。$U’^{(k)}$ ではなく $U^{(k)}$ が正しい。
(10.7) を解いている過程の特性根の表式で、ルート内は $1-4pqs$ ではなく $1-4pqs^{2}$ が正しい。また、当然ながら $2$ 式が同じになってしまっているのはおかしくて、$2$ 行目は左辺は $\lambda_{2}$ で右辺のルートの前の符号は $-$ である。
前項と同様のことが、$V(z,s)$ の方についても言える。

すると、$p=q=\frac{1}{2}$, $a=m$ により
\begin{align*}
\lambda_{1} = \mu_{1} &= \frac{1+\sqrt{1-s^{2}}}{s} \\
\lambda_{2} = \mu_{2} &= \frac{1-\sqrt{1-s^{2}}}{s}
\end{align*}
であって
\begin{align*}
U(z,s) &= \frac{\lambda_{1}^{m-z} – \lambda_{2}^{m-z}}{\lambda_{1}^{m} – \lambda_{2}^{m}} \\
V(z,s) &= \frac{\lambda_{1}^{z} – \lambda_{2}^{z}}{\lambda_{1}^{m} – \lambda_{2}^{m}}
\end{align*}
である（$p=q$ により、$\lambda_{1}\lambda_{2}=1$ であることに注意）。よって
\begin{align*}
u(1,n) &= \frac{1}{n!} U^{(n)}(1,0) \\
&= \frac{1}{n!} \Bigl( \frac{\partial}{\partial s} \Bigr)^{n} U(1,s) \Bigr\lvert_{s=0} \\
v(1,n) &= \frac{1}{n!} V^{(n)}(1,0) \\
&= \frac{1}{n!} \Bigl( \frac{\partial}{\partial s} \Bigr)^{n} V(1,s) \Bigr\lvert_{s=0}
\end{align*}
から
\begin{equation}
\label{eq:circular-randomwalk-38}
a_{n} = \frac{1}{n!} \Bigl( \frac{\partial}{\partial s} \Bigr)^{n} \bigl( U(1,s) + V(1,s) \bigr) \Bigr\lvert_{s=0}
\end{equation}
だということになる。一方、上で固有値・固有ベクトルを使って繰り広げた計算中で、\eqref{eq:circular-randomwalk-15}辺りから先の式を利用すると
\begin{equation}
\label{eq:circular-randomwalk-39}
a_{n} = \frac{1}{m}\Bigl( \sin^{2}\frac{\pi}{m} \cos^{n-1} \frac{\pi}{m} + \sin^{2} \frac{3\pi}{m} \cos^{n-1} \frac{3\pi}{m} + \dots + \sin^{2} \frac{(2m-1)\pi}{m} \cos^{n-1} \frac{(2m-1)\pi}{m} \Bigr)
\end{equation}
なので、\eqref{eq:circular-randomwalk-38}の右辺と\eqref{eq:circular-randomwalk-39}の右辺の値が $m$, $n$ によらず等しい、という非自明な結果が得られたことになる。$U(1,s)$, $V(1,s)$ の微分は、具体的な $n$ に対してさえ結構ハードな計算になるので、手計算で検算するのは私には無理っぽい…。できれば maximaを使って検算したかったのだが、うまく使えずに断念した。簡単にわかるのは

$\lambda_{1}$, $\lambda_{2}$ は $s$ の奇関数
よって $U(1,s)$ は奇関数、$V(1,s)$ の偶奇性は $m$ の偶奇と一致
すると $u(1,n)$ は $n$ が偶数だと $0$, $v(1,n)$ は $n$, $m$ の偶奇が一致すると $0$

程度だ。【追記】ああそうか、期待値は $\frac{\partial U}{\partial s}(1,s) \Bigr\rvert_{s=1}$, $\frac{\partial V}{\partial s}(1,s) \Bigr\rvert_{s=1}$ を通じて計算できますね…。実際には $s\to 1$ の極限をとる必要がありますが、今チョロチョロっとメモ程度の計算で片付けようとしたら意外と面倒だったので、今度時間のある時にちゃんと $E=m$ になるかどうか検算しておきます。
→うまく行きますね。
\[ \frac{\partial U}{\partial s}(1,s)\Bigr\rvert_{s=1} + \frac{\partial V}{\partial s}(1,s) \Bigr\rvert_{s=1} = m-1 \]
となって、これと
\[ a_n = u(1,n) + v(1,n), E = \sum_{n=2}^{\infty} n a_{n-1} = \sum_{n=1}^{\infty} (n+1)a_n \]
を合わせると $E = m-1 + 1 = m$ となっています。一安心。

■ 経路数問題への言い換え

さて、実は「$1$ 次元の有限格子上のランダムウォークと同じ」ということに気づいた後も、結構長い間「破産の確率と同じ」ということまでには気づかなかった（←マヌケ！）。その間は、以下のような「経路数」に関する考察が有力なアプローチだと見て色々考えており、実際 $a_{n}$ の一般項のさらに別の表式も出ていたので、それについても述べておく。これが、本記事冒頭付近で触れた「数学ガール」で引っかかっていた問題の解決につながった考察なのだ。そういう意味では、私の知識が狭くてここまでのような結果が当初見えなかったことは、怪我の功名的な不幸中の幸いの面があった。

まず、$1$ 次元の $2$ と $m$ の間のみのランダムウォークで、$n$ 歩進む時の $2 \to 2$, $2 \to m$ の経路数が求まれば、$a_{n}$ は表せる（※ ここからは $m>2$ としておく）。より正確には、この $1$ 次元の有限の鎖上で、$1$ 回目に $2$ にいるとして、$n$ 回目までに $1$ を一度も通らずに $n$ 回目にまた $2$ にいる経路数が $x_{n}$ 通りあるすると、元の問題では
\[ \text{「$1$から$1$回目に$2$に出て、$n$回目までに一度も$1$に戻らず、$n$回目に$2$にいる確率」} = \frac{x_{n}}{2^{n}} \]
である。

同様に、$1$ 回目に $2$ にいて $n$ 回目に $m$ にいる経路数が $y_{n}$ 通りあるとすれば、元の問題では
\[ \text{「$1$から$1$回目に$2$に出て、$n$回目までに一度も$1$に戻らず、$n$回目に$m$にいる確率」} = \frac{y_{n}}{2^{n}} \]
である。

対称性によって、これらはそれぞれ $1$ から $1$ 回目に $m$ に出た場合の確率にもなっているので、
\begin{equation}
\label{eq:circular-randomwalk-22}
a_{n} = \underbrace{\frac{x_{n}}{2^n}}_{1\to2\to2\text{の確率}} + \underbrace{\frac{y_{n}}{2^{n}}}_{1\to m\to2\text{の確率}} = \frac{x_{n}+y_{n}}{2^{n}}
\end{equation}
となっている。よって、有限長 $1$ 次元ランダムウォークの問題の経路数 $x_{n}$, $y_{n}$ が求まれば、$a_{n}$ の厳密な表記が得られることになる。

この経路数の問題には既視感がある。頂点 $1$ は通らない、ということは、どの時点でも右向き移動の累計回数が左向き移動の累計回数以上であることが最低限必要で、この条件だけならカタラン数でも出てきた。ということは、カタラン数を求めるときの手法が参考になるのではないか…？

早速やってみよう。

◇ カタラン数の求値技法の利用

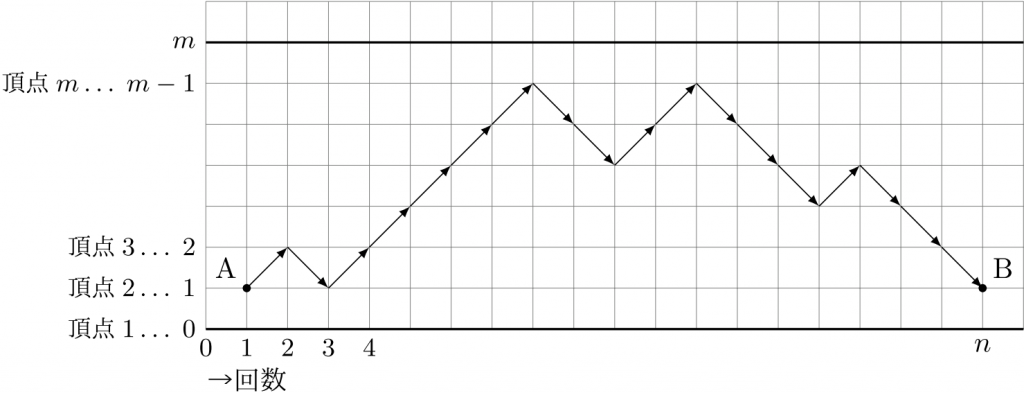
$1$ 次元のランダムウォークの経路は、横軸に回数、縦軸に頂点番号を取れば、図のような $\nearrow$ と $\searrow$ をつなげた折線で表せる。ここでは頂点番号と $y$ 座標が $1$ ずらしてあるので、頂点 $2$ と $m$ の間だけで動くことは、折線が $y=0$ にも $y=m$ にも触れない、ということとして表せる。

まず $x_{n}$ から考えよう。$1$ 回目に $2$ にいて、$n$ 回目にまた $2$ に戻ってくる経路というのは、図のように $\text{A}(1,1)$ から $\text{B}(n,1)$ までの折線に対応する。この折線上の矢印の個数は $n-1$。$\nearrow$ と $\searrow$ の個数は等しくないといけないから、$n-1$ が偶数のときのみこのような折線はありえて、$n=2k+1$ とおける。もし、折線に何の制限もなければ、その本数は図の青線のような $k \times k$ の正方格子を A から B まで進む最短経路の本数で
\begin{equation}
\label{eq:circular-randomwalk-23}
\kumiawase{2k}{k}
\end{equation}
通りである。

しかし、これだと実際には $y=0$ や $y=m$ にぶつかってしまう折線もあるので、不適な折線は除かなければいけない。$y=0$ にぶつかってしまうものの個数については、次のような標準的な数え方があった。

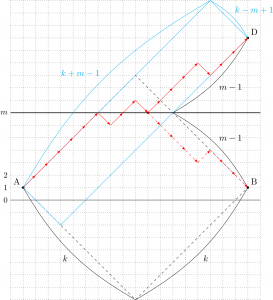
折線が最初に $y=0$ にぶつかる点より手前の部分を、$y=0$ に関して折り返すと、点 $\text{C}(1,-1)$ からその点までの折線になって、それを残った部分とつなげると、C から B までの折線になる。
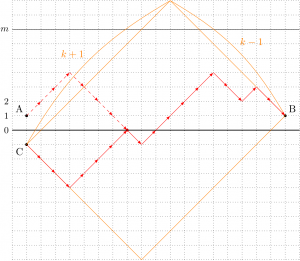
逆に、C から B までの折線をひとつ決めると、初めて $y=0$ とぶつかる点から手前を同じように $y=0$ に関して折り返して、A から B までの折線（のうち $y=0$ にぶつかるもの）が作れる。

以上のことから「A から B までの折線のうち、$y=0$ にぶつかるもの」（このような折線全体の集合を $X$ としておく）と「C から B までの折線」の間には 1 対 1 の対応が作れるので、その個数は同数。後者は、図のオレンジ色の $(k+1) \times (k-1)$ の長方形の格子の C から B までの最短経路として数えることができるので、
\begin{equation}
\label{eq:circular-randomwalk-18}
\underbrace{\#(X)}_{\text{集合$X$の要素数}} = \kumiawase{2k}{k-1}
\end{equation}
通り。（ただし、ここまでの議論は暗黙のうちに $k>0$ を仮定していた。$k=0$ のときは $\text{A}=\text{B}$ で、$y=0$ にぶつかる経路は存在しないので、$0$ 通りとすべきである。したがって、標準的な慣習通り、二項係数について
\begin{equation}
\label{eq:circular-randomwalk-21}
\kumiawase{\square}{\text{負の数}} = \kumiawase{\square}{\text{$\square$より大きい数}} = 0
\end{equation}
という約束を採用することにすれば、\eqref{eq:circular-randomwalk-18}は $k=0$ のときも含めてなりたつ）

カタラン数を求める場合は、ここまでの考察で十分で、「A から B までの折線のうち、$y=0$ にぶつからないもの」の本数は
\[ \eqref{eq:circular-randomwalk-23} – \eqref{eq:circular-randomwalk-18} = \kumiawase{2k}{k} – \kumiawase{2k}{k-1} \quad
\Bigl( = \dfrac{\kumiawase{2k}{k}}{k+1} \Bigr) \]
だった。今回の問題では、さらに「$y=m$ にぶつからない」という条件も考えなければならない。

「A から B までの折線のうち、$y=m$ にぶつかるもの」の集合を $Y$ としよう。このような折線は、「最後に $y=m$ とぶつかる点から後を $y=m$ に関して折り返す」ことによって、「A から $\text{D}(1,2m-1)$ までの折線」と 1 対 1 に対応するので、図よりその本数は
\begin{equation}
\label{eq:circular-randomwalk-19}
\#(Y) = \kumiawase{2k}{k-m+1}
\end{equation}
通りである。

ただし、この図は $k \geqq m-1$ を暗黙のうちに仮定しており、$k < m-1$ のときは $Y$ は空集合である。その場合も約束\eqref{eq:circular-randomwalk-21}によって\eqref{eq:circular-randomwalk-19}は正しい。

さて、これで $y=0$ や $y=m$ に触れてしまう不適な折線 $X$, $Y$ の個数がわかったわけだが、まだ $x_{n}$ を
\[ \eqref{eq:circular-randomwalk-23} – \eqref{eq:circular-randomwalk-18} – \eqref{eq:circular-randomwalk-19} = \kumiawase{2k}{k} – \kumiawase{2k}{k-1} – \kumiawase{2k}{k-m+1} \]
と計算するわけにはいかない。不適な折線の全体は $X \cup Y$ だが、$X \cap Y = \emptyset$ とは限らないからだ。正しくは
\begin{align*}
x_{n} &= \eqref{eq:circular-randomwalk-23} – \#(X \cup Y) \\
&= \kumiawase{2k}{k} – (\#(X) + \#(Y) – \#(X \cap Y)) \\
&= \kumiawase{2k}{k} – \kumiawase{2k}{k-1} – \kumiawase{2k}{k-m+1} + \#(X \cap Y)
\end{align*}
と計算しなければならない。

ところがこの $\#(X \cap Y)$ の計算が難物だ。$X \cap Y$ というのは「A から B への折線で、$y=0$ にも $y=m$ にも触れるもの」の集合だが、当初はこれを次の２つの合計で数えられると思ってしまっていた。

先に $y=0$ に触れ、後から $y=m$ に触れるもの
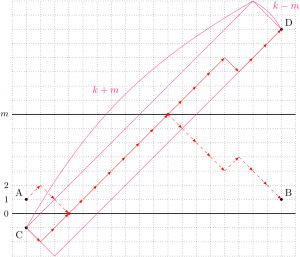C から D への折線と同数で $\kumiawase{2k}{k-m}$ 本
先に $y=m$ に触れ、後から $y=0$ に触れるもの
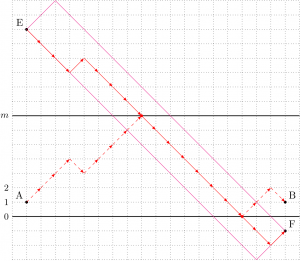E から F への折線と同数で、やはり $\kumiawase{2k}{k-m}$ 本

こう思い込んだまま一度はこの記事を書き始めてしまい、$y_{n}$ も同様の考えに基づく式を出して $a_{n}$ の一般項が求まった…！という話にしかかっていたのだが、念のために maximaで「そうやって求めた値」と「漸化式でちゃんと求めた値」を計算させて比べてみると、$n$ が $2m$ を超える辺りでずれが出始めて、ようやく誤りに気づいた。

とっくにおわかりの方も多いだろうが、上の考えのどこが間違っているかというと、$k$ が大きくなってくると、C→D の折線の中に、$y=0$ で折り返すと、$y=0$ より先に $y=m$ に触れてしまうものが出てくるのだ。E→F の折線も同様で、$y=m$ で折り返すと先に $y=0$ に触れてしまうものも出てくる。つまり、上のように数えてしまうと、本来の $\#(X \cap Y)$ よりも大きい値が出てきてしまう。

これの補正は（ちょっと考えただけでは）困難だ。また別のアプローチを考えてみることにする。

◇ 書き込み方式と鏡像法

今度は、経路数を書き込み方式で書いてみよう。後の話の都合上、これまでの図とは縦と横を入れ替える。やはり $m=7$ の場合を例にとる。

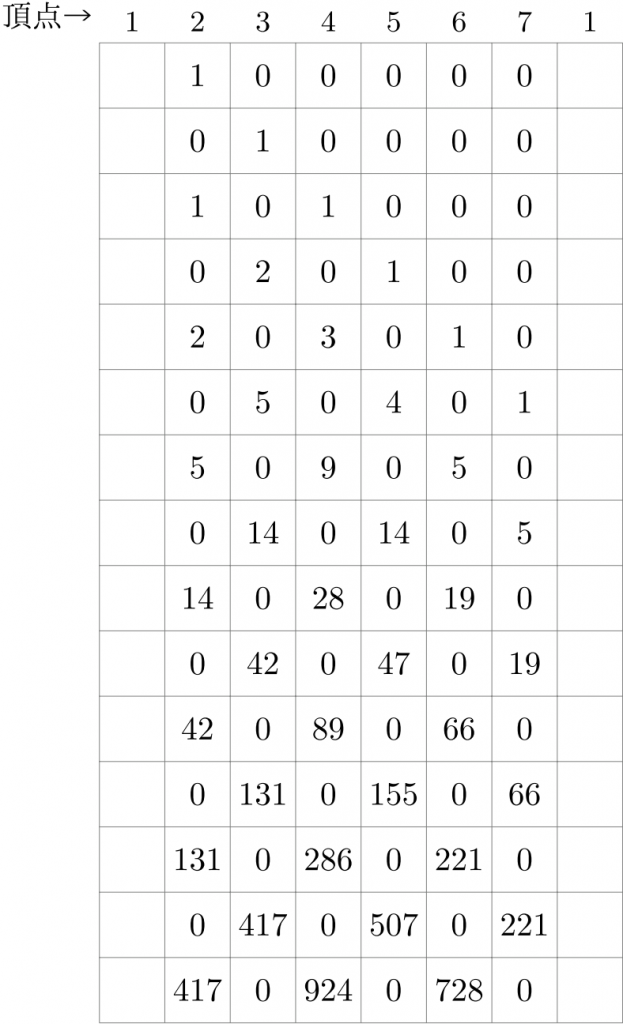
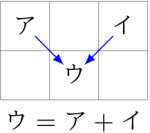
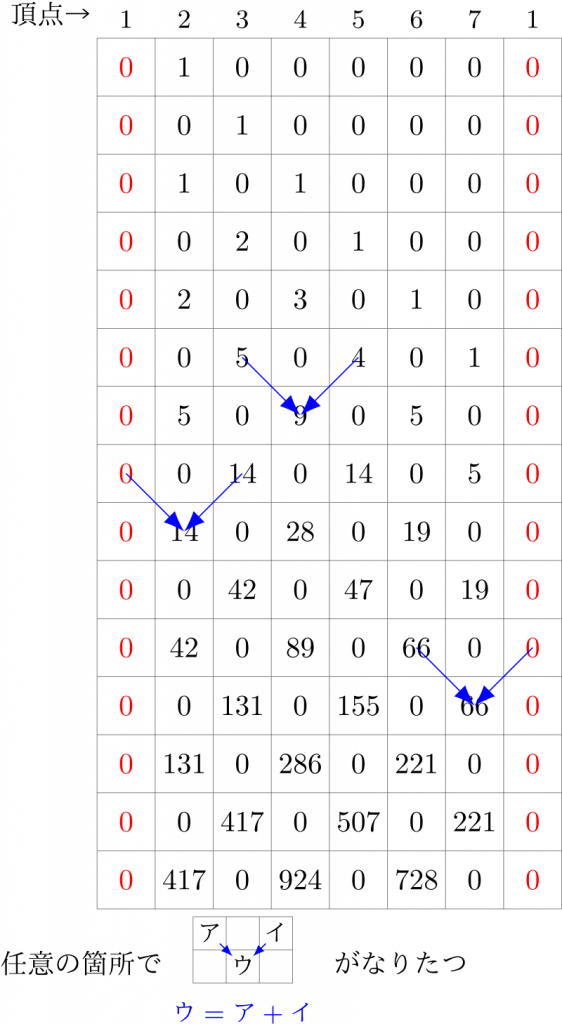
先ほどの図では、格子の「交点」が「各時刻での各頂点」を表していたが、今度はそうではなく、格子線で囲まれた「枠（欄）」が「各時刻での各頂点」を表していることに注意して頂きたい。各欄に書き込まれた数が「その時刻にその頂点に至る経路数」である。最上段が $1$ 回目の経路数で、ここでは頂点 $2$ だけが $1$ 通り、他の頂点は当然 $0$ 通りである。以下、$2$ 段目、$3$ 段目…がそれぞれ $2$ 回後、$3$ 回後…の経路数である。$2$ 段目以降は、Pascal の三角形と類似した法則で決まっていくことがわかるだろう。原則として、「右上」と「左上」の数の和が各マスの数字になる。

違うのは、頂点 $1$ に達しない経路数を数えているので、頂点 $2$ を「ウ」として計算するときは「左上」の「ア」がなくて「イ」がそのまま「ウ」となること、頂点 $7$ も同様になることだ。

これを眺めてみると、頂点 $2$ や $7$ も含めて Pascal の三角形の法則を成立させるのは容易であることに気づく。「頂点 $1$ の経路数は常に $0$ とする」と約束すればいいのだ。

これを見ながら、「そう言えば、Pascal の三角形と言えば、以前Legendre 多項式で表される確率・その２で思いついたり、算数エッセー「新編算数学入門」第70回重ね合わせの原理～「パスカルの三角形の発展問題」について～で読んだりした通り、重ね合わせの原理が成立していたな…。これが何かうまく使えないだろうか」と考えていたところ、次のようなことを思いついた。

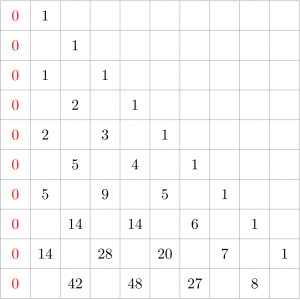
まずは簡単のため、「$y=m$ に達しない」という条件は一旦外し、「$y=0$ に達しない」という条件だけで経路数を考えてみよう。これは、当然ながらカタラン数を考えたときと同じ設定である。左端に並ぶ「境界条件」の $0$ 以外の $0$ は省略して書くと、こんな図になる。

左端の $0$ の隣の列に並ぶ $1,1,2,5,14,\dotsc$ がカタラン数になるわけである。ここで、「重ね合わせによって、左端での境界条件:定数 $0$ を実現できないか？」と考えてみると、それは容易であることにすぐ気づくだろう。最上段の「初期値」$1$ と対称な位置に、ちょうど $-1$ 倍の初期値を置いてやればいいのだ。

つまり、$x=0$ での境界条件を要請する代わりに、Pascal の三角形の法則が $x<0$ も含めて成り立っているとして、最上段の $x= \pm 1$ の所にそれぞれ初期値 $\pm 1$ を置いてやればいい。Pascal の三角形の法則は線形漸化式なので、この場合の解は最上段に $+1$ だけがある時の解と $-1$ だけの解があるときの重ね合わせになるので、$x=0$ では自動的に常に $0$ になるわけだ。

この重ね合わせの原理によって、カタラン数の値はすぐ立式できる。例えば丸をつけたカタラン数 $14$ は、右側の「$+1$」が作る解の Pascal の三角形の値 $\kumiawase{8}{4}$ と、左側の「$-1$」が作る Pascal の三角形の値 $-\kumiawase{8}{3}$ を合わせたものだから、$\kumiawase{8}{4} – \kumiawase{8}{3}$ と立式できる。このように、カタラン数の一般項 $c_{k} = \kumiawase{2k}{k} – \kumiawase{2k}{k-1} = \frac{\kumiawase{2k}{k}}{k+1}$ は、Pascal の三角形の法則の線形性と重ね合わせの原理からも導くことができるのだ。

…これを思いついたときは「おお、なかなかしゃれた導出が見つかったではないか。カタラン数のこういう導出って、結構オリジナルなのでは？よし、blog 記事にもってこいのネタができた（笑）」と悦に入っていたのだが、たまたま同期時に職場で「大学への数学」のバックナンバーをめくっていたら、2004年の栗田さんの連載で紹介されていて、しかもそこの記事によると森重文さんがその時点での数年前にある講演で紹介していてその筋の人々の間で評判になっていた、ということだったので、何のことはない、私の「発見」なんてものは干支まる一回り分以上も遅れたものに過ぎなかった…というオチがついた（笑）。

【2019,8/18 追記】ああ、この話、「解法の探求・確率」新版の「カタラン数」のページで紹介されていたんですね。私が持ってるのは旧版で、そっちだとその部分は別の話（逆ポーランド記法のカッコの付け方の数え方）になっていたので気づいてませんでした。そして森重文さんがこの数え方に気づいていたのは、高校生の時だったのですか（笑）。

さて、この「$x=0$ で $0$ という境界条件をみたすために、対称な位置に $-1$ 倍の初期値を置く」という考え方、どこかで見た覚えはないだろうか。私は、これを思いついたときに、「あ、これ鏡像法じゃん」と思った。

電磁気を学習された方は、静電場の単元で「電荷分布が決まっており、あらかじめ決められた位置に導体面が配置され、さらに個々の導体面の電位も決まっている」という条件のもとでの静電ポテンシャル（電位場） $\phi$ を求めたい時に、特殊な場合には導体を仮想的な点電荷で置き換えることで厳密解が求められることがある（偏微分方程式を解かなくても）…という解法を習った覚えはお持ちでないだろうか。例えば、無限平面の導体と 1 個の点電荷があるときの $\phi$ は、導体面に関して対称な位置に逆符号で同絶対値の点電荷があるとし、導体面を取り去った状態の $\phi$ と同じになる…という奴だ。鏡像法は、Poisson 方程式（の左辺の Laplace 演算子）の線型性（及び、電荷分布と境界条件を指定したときの解の一意性）を利用していたわけだが、上のカタラン数の求め方も根っ子にある考え方は通底していて、Pascal の三角形の法則の線型性（と、解が初期値から一意に決まること）を利用していたわけだ（※ Poisson 方程式が楕円型の偏微分方程式であるのに対し、Pascal の三角形の法則は「時間と共に空間内に影響が伝搬していく」様子を表す拡散方程式や波動方程式（これは当然、放物線型や双曲線型の偏微分方程式）の類似品であることを考えれば、実は両者は結構性質が違っており、同じように扱うのは雑かもしれません。ただ、最初にこの類似性が頭に思い浮かんだときは、そんなことにはまったく考えが及びもせず、頭の中では「よく似ている！」という発見の喜びばかりが先行して渦巻いていました）。

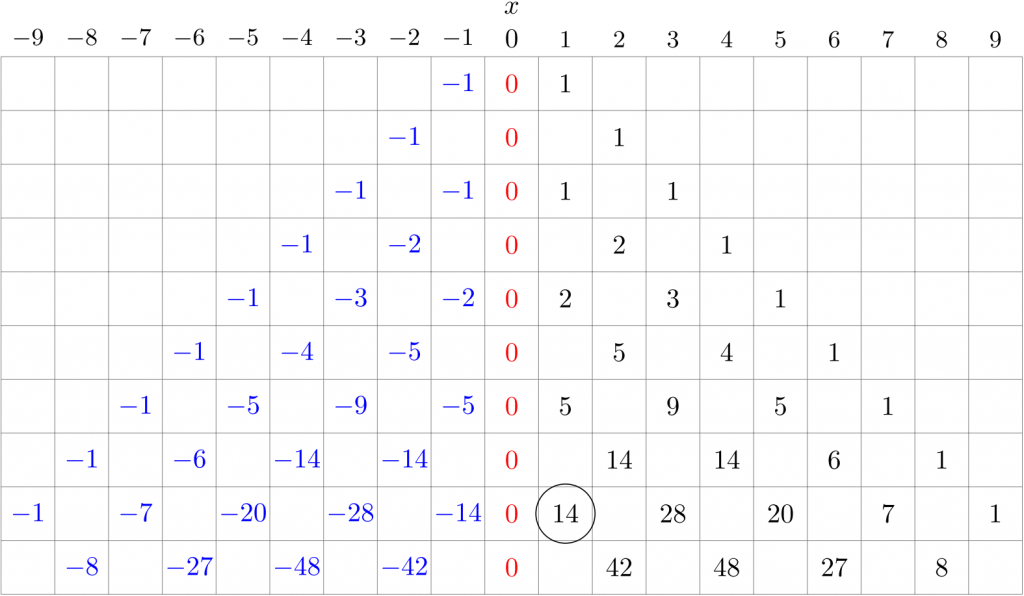
話を元に戻す。カタラン数がこうやって鏡像法の考えで求められるなら、元々考えていた「$y=0$ にも $y=m$ にも触れない経路数」も同じように鏡像法を使って求められないだろうか？

今、「$x=0$ で $0$」という境界条件を再現するために $x=0$ に関して対称な位置に逆符号の電荷、じゃなかった、初期値を置いたが、「$x=0$, $x=m$ の両方で $0$」という境界条件を再現するには、素朴に考えると $x=0$, $x=m$ の両方について対称になるように正負の初期値を配置すればよいはずだ。そうすれば、$x_{n}$ や $y_{n}$ を表す式が手に入ることになる。問題は、カタラン数の時と違って、対称面が $2$ 枚になったので、配置する正負の電荷——もう電荷でいいや——が無限個必要になり、果たして矛盾なくそのような配置を実現できるだろうか？ということを考える必要が出てくるところだ。

「無限個必要になる」というのがピンと来ない方もいるかもしれないので、どういうことか説明しておく。

元々の $x=1$ の $+1$ という電荷以外に、$x=-1$ に置く $-1$ という電荷に対しても、$x=m$ に関して対称な位置に逆符号の電荷を置く必要がある。
すると、そうやって置いた電荷に対しても、$x=0$ に関して対称な位置に逆符号の電荷を置く必要がある。
すると、それらの電荷に対しても、$x=m$ に関して対称な位置に逆符号の電荷を置く必要がある。

以下同様の繰り返しが無限に続くことは容易にわかる。一般に、平面図形で、線対称の対称軸が複数存在し、互いに平行な場合は必ず無限に存在しないといけないことが言えるが、それと同様なことが起きているわけだ。

ともかく、上の考えに従って $+1$, $-1$ の電荷を配置していってみると、どうやらこうなっているらしいことが見えてくる。
\begin{equation}
\label{eq:circular-randomwalk-20}
x= 2sm \pm 1 \text{ に } \pm 1 \text{ の電荷を置く（複号同順）} \quad (s=0, \pm1, \pm2, \dotsc)
\end{equation}
逆に、\eqref{eq:circular-randomwalk-20}のときちゃんと $x=0$, $x=m$ の両方について対称な電荷分布になっているかどうか検証してみよう。まず、$x=\pm1$ に置かれている $\pm1$ の電荷は確かに $x=0$ について対称である。次に、$x=\pm (2m-1)$ に置かれている電荷は $\mp1$（複号同順）となるので、これらも $x=0$ に関し対称。さらに $x= \pm (2m+1)$ に置かれている電荷は $\pm1$（複号同順）だから、これらも $x=0$ について対称だ。以下すべて $x=0$ に関し対称、とわかる。

続いて、$x=m$ に関する対称性を検証しよう。まず、$x=1, 2m-1$ の電荷はそれぞれ $\pm1$ だから確かに $x=m$ について対称。さらに、$x=-1,2m+1$ の電荷はそれぞれ $\mp1$ だからやはり $x=m$ について対称。このように、「足して $2m$ になる 2 つの $x$ 座標」どうしをペアにして考えていくと $x=-2(s-1)m-1, 2sm+1$ の電荷がそれぞれ $\mp1$, $x=-2(s-1)m+1, 2sm-1$ の電荷がそれぞれ $\pm1$ なので、やはりちゃんと対称になっていることがわかる。

と、いうことは。

この無限個の $\pm1$ の電荷——いやさ、初期値配置によって、懸案だった $x_{n}$, $y_{n}$ の表式が得られるはず、ということだ。

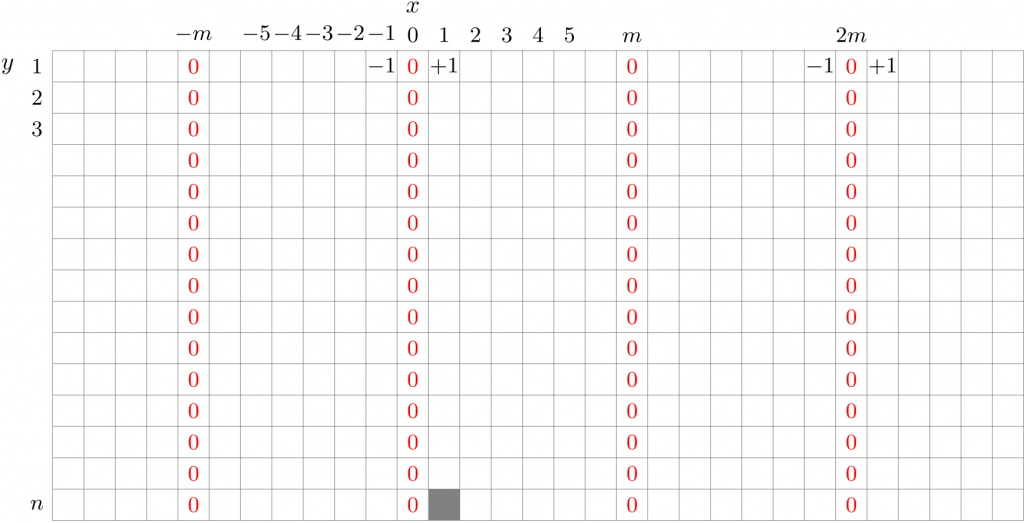
まず $x_{n}$ は、図のグレーの点 $(1,n)$ に、各初期値の点 $(2ms\pm1,1)$ から $\searrow$ と $\swarrow$ で到達できる経路数を符号付きで足し合わせたものになる。$X=2ms\pm1$ とおき、$\searrow$ を $a$ 個、$\swarrow$ を $b$ 個並べるとすると、
\begin{align*}
a+b &= n-1 & a-b &= 1-X \\
\therefore a &= \frac{n-X}{2} & b &= \frac{n+X-2}{2}
\end{align*}
となる。$X=2ms \pm 1$ が奇数だから、$n$ が奇数のときのみ適する $a,b$ が存在し、$n=2k+1$ とおくと
\[ a = \frac{2k+1-(2ms \pm 1)}{2},\quad b= \frac{2k-1+ 2ms \pm 1}{2} \]
である。すなわち、複号の上を取れば
\[ a = k-ms, \quad b= k+ms \]
で、複号の下を取れば
\[ a = k-ms+1, \quad b=k+ms-1 \]
というわけだ。これらから $x_{n}$ への寄与は $\pm \kumiawase{a+b}{a}$ となるので、あとは $s$ に関して和を取るだけだ。

$n$ が偶数の場合も合わせてまとめると、
\begin{equation}
\label{eq:circular-randomwalk-24}
x_{n} = \begin{cases}
0 & (\text{$n$が偶数のとき}) \\
\sum_{s \in \mathbb{Z}} \bigl( \kumiawase{n-1}{k-ms} – \kumiawase{n-1}{k-ms+1} \bigr) & (\text{$n$が奇数のとき; $n=2k+1$})
\end{cases}
\end{equation}
という結果になる。特に、$s=0$ からの寄与がもちろんカタラン数だ。なお、静電場での本当の鏡像法でも、導体面が複数存在する場合には無限個の鏡像で置き換えることにより解が得られる（例えば、ファインマン物理学を見よ）ので、\eqref{eq:circular-randomwalk-24}はそのアナロジーになっている。

\eqref{eq:circular-randomwalk-24}は無限和になっているが、これは形式的なものに過ぎない。$n$ を決めると二項係数が意味を持つ $s$ の個数は常に有限個しかないので、具体的な値を計算する場合は有限和になる。よってこの（形式的）無限和は必ず収束する。

同様にして、$y_{n}$ も形式的無限和で表せる。こちらは、$(2ms\pm1,1)$ から $(m-1,n)$ までの経路数を符号付きで重ね合わせれば得られる。途中の計算は $x_{n}$ と概ね同じなので省略すると、今度は $n-m$ が奇数のときのみ適する経路が存在し、$n-m=2l-1$ とおくと
\begin{equation}
\label{eq:circular-randomwalk-25}
y_{n} = \begin{cases}
0 & (\text{$n-m$が偶数のとき}) \\
\sum_{s \in \mathbb{Z}} \bigl( \kumiawase{n-1}{l+ms} – \kumiawase{n-1}{l+ms-1} \bigr) & (\text{$n-m$が奇数のとき; $n=m+2l-1$})
\end{cases}
\end{equation}
となっている。

これで、$a_{n}$ の一般項が、実質有限和の形式的無限和という形を通しても求まったことになる。それは、\eqref{eq:circular-randomwalk-22}によって
\begin{align}
a_{n} &= \frac{x_{n}+y_{n}}{2^{n}} \notag\\
&= \frac{1}{2^{n}} \left[ \begin{gathered}
\left\{ \begin{aligned}
0 & (\text{$n$が偶数のとき}) \\
\sum_{s \in \mathbb{Z}} \bigl( \kumiawase{n-1}{k-ms} – \kumiawase{n-1}{k-ms+1} \bigr) & (\text{$n$が奇数のとき; $n=2k+1$})
\end{aligned} \right\} +\\
\left\{ \begin{aligned}
0 & (\text{$n-m$が偶数のとき}) \\
\sum_{s \in \mathbb{Z}} \bigl( \kumiawase{n-1}{l+ms} – \kumiawase{n-1}{l+ms-1} \bigr) & (\text{$n-m$が奇数のとき; $n=m+2l-1$})
\end{aligned} \right\}
\end{gathered} \right]
\label{eq:circular-randomwalk-26}\end{align}
のように表される、というわけだ。

これも、上で陥ったような見落としがないかどうか心配だったのだが、再度 maxima を使って、$m=7$ の場合に「\eqref{eq:circular-randomwalk-24}, \eqref{eq:circular-randomwalk-25}による計算値」と「Pascal の三角形の法則と境界条件によって漸化式から計算した経路数」と比較したところ、$n=500$ までは合致していたので、今度こそ正しい式の導出に成功していると思う。

\eqref{eq:circular-randomwalk-26}が、\eqref{eq:circular-randomwalk-38}や\eqref{eq:circular-randomwalk-39}と一致する、ということは、背景を知らなければそう簡単には気づかない関係だろう。

さて、今見たような「無限個の鏡像点を置いた経路数の算出法」も別に本記事のオリジナルの技法というわけではない。
http://www.jams.or.jp/kaiho/kaiho-88.pdf
に「寄稿」として収録されている「Catalan 数の一般化 — 格子経路組合せ論からの Approach —」の式(5)がまさしくここでの $x_{n}$, $y_{n}$ の一般化になっていることに後から気づいた。そこでは 1844 年の L.Ellis からの引用とされているので、上の計算は170年ほど遅れてやっと追いついたものに過ぎない（あと、これもやはり組み合わせ論をやっている方からするとよく知られた何の新規性もない話ではなかろうか、と思っている所である）。

ちょっと脱線するが、実は上記の「Catalan 数の一般化」の PDF を発見・入手したのは今回のことではない。以前 Legendre 多項式で表される確率で、階乗を使ったややこしい和で表される経路数が、なぜか Legendre 多項式の特殊値で表される、という現象に遭遇したときに、その理由がどこかで解明されていないかと類似の式を探し回ったときに見かけて保存しておいた資料だった。その時は、式(15)の次の行がその時のテーマの式と特殊関数の使い方がよく似ていて（少なくとも見かけだけは）、「Legendre 多項式と Chebyshev 多項式の違いはあれ、何か参考にはなるかもしれない」と思って保存しておいた資料だ（結局、その時の一連の考察には本質的には役立てられなかったが）。それを今回ざっと読み返してみた所、式(5)で $x_{n}$, $y_{n}$ の一般化がとっくに出ていたことに気づいてひっくり返った次第だ。

◇ 「数学ガール」のピアノ問題の拡張の解決

さて、こんな具合に求めた $x_{n}$, $y_{n}$ の（和を使った）一般項だが、この導出の最中で、この考え方を使って「数学ガール」乱択アルゴリズム編の「ピアノ問題」を拡張した「制限付きピアノ問題」の解を求められる、ということに気がついた。

この節は、「数学ガール」乱択アルゴリズム編をお持ちでない方にはおそらくわからない内容になってしまうであろうことをお断りしておく。その拡張が何で重要かというと、同書では「ピアノ問題」の一般解を後の方の 3-SAT の乱択アルゴリズムの確率評価に生かしており、その評価は「制限付きピアノ問題」の解がわかっていればより精密化できるはずだったからだ。

「数学ガール」乱択アルゴリズム編の「ピアノ問題」とは、次のような問題だ（同書 p.304 より）。

開始音より低い音を使わず、隣接した音を $a+b$ 個つなぎ、開始音よりも$a-b-1$ 音だけ高い音で終わるメロディの個数はいくらか

同書では、この問題に対して、カタラン数の求め方と同様な解法で、経路数の差として捉え、$2$ つの二項係数の差によって一般解を与えている。そして、この結果は更に後の p.374 で、3-SAT を解く乱択アルゴリズムの性能評価の過程で使われている。これを使って、「ハミング距離が $m$ の状態から始めて、$a^{*}$ に至るまでの途中で、合計でちょうど $i$ 回遠ざかる方に動いてしまう経路数」を求めていることになっている（※ 文字の使い方は「数学ガール」の方に合わせたので、ここでの $m$ はこれまで使っていた $m$ とは別のもの）。

しかし、ハミング距離というものは、定義により $n$ より大きくはならないので、途中で距離が $n$ を超えてしまうような経路は実際には存在しないはずだ。つまり、$m+i>n$ となるような $m$, $i$ に対しては、ピアノ問題の一般解を使うと「本来不適な経路」も算入してしまうため、経路数が過大評価になってしまう。これだと、p.375 最初の不等式は意図している「$P(m,i)$ の下からの評価」になっていない恐れがある（右辺が、$P(m,i)$ の真の値を上回ってしまっているかもしれない）。（※ この不等式には他にも怪しい所があり、実はそれを含めて考えると、結局はこのことを考えなくても $Q(m)$ に対しては正しい評価になっているのかもしれないのだが、それは今回の本題ではないのでおいておく）

距離が $n$ を超える経路を除くということは、ピアノ問題の言葉で言えば「使える音階の高さに上限があるような『制限付きピアノ問題』」を考えるということだ。これは、鍵盤の長さが有限、と考えれば自然なモデルだ。数年前、このことについて著者の結城浩さんに問い合わせた時には「（果たしてそんなものに閉じた形の式で表せる答があるのかどうかは、不勉強で知りません…）」と自己評価していたのだが、本記事の「無限個の電荷による鏡像法」はまさしくその「制限付きピアノ問題」に対する答を与えられる技法になっている。\eqref{eq:circular-randomwalk-23}の上のような図で、「$y=0$ にも $y=m$ にも触れない経路数」を求めようとしているのだから…！そこの図では、経路の終点が点 B であるものを考えていたわけだが、終点の $y$ 座標は調節が効く。なぜならば、\eqref{eq:circular-randomwalk-20}の上の図に翻訳したとき、終点はグレーの点に限定する必要はなく、$(1,n)$〜$(m-1,n)$ のどこにあったとしても、$x_{n}$, $y_{n}$ を求めるときと同様の考え方で経路数は出せるのだから。

途中の計算は省くが、実際に求めてみると、「距離 $m$ から始まって、途中で合計ちょうど $i$ 回だけ遠ざかる向きに進み、距離が一度も $n$ を超えることなく $0$ に到達する経路数」は次のようになった。
\begin{equation}
\label{eq:circular-randomwalk-27}
\sum_{s \in \mathbb{Z}} \Bigl( \kumiawase{m+2i-1}{m+i-(n+1)s-1} – \kumiawase{m+2i-1}{m+i-(n+1)s} \Bigr) = \sum_{s \in \mathbb{Z}} \frac{m-2(n+1)s}{m+2i} \kumiawase{m+2i}{i+(n+1)s}
\end{equation}
この被和項 $\frac{m-2(n+1)s}{m+2i} \kumiawase{m+2i}{i+(n+1)s}$ は、$s=0$ の時確かに「数学ガール」での経路数と一致している。

ここで、「数学ガール」では確率を下から評価するため $i \leqq m$ となる $i$ の経路のみを考えていたことを使うと、\eqref{eq:circular-randomwalk-27}の形式的無限和を具体的な有限和に直せる。\eqref{eq:circular-randomwalk-27}の二項係数が意味を持つような $s$ の範囲を求めると、
\begin{gather}
0 \leqq i+(n+1)s \leqq m+2i \notag\\
\label{eq:circular-randomwalk-28}
\therefore -i \leqq (n+1)s \leqq m+i
\end{gather}
でなければならない。$i \leqq m \leqq n$ を使うと、\eqref{eq:circular-randomwalk-28}より
\[ -n \leqq (n+1)s \leqq 2n \]
となるから、$-1$ 以下の $s$ は不適だし、$2$ 以上の $s$ も不適である。よって、\eqref{eq:circular-randomwalk-27}の和は $s=0, 1$ の項のみ残したものと同じで、
\begin{equation}
\label{eq:circular-randomwalk-29}
\eqref{eq:circular-randomwalk-27} = \underbrace{\frac{m}{m+2i} \kumiawase{m+2i}{i}}_{\text{$s=0$の項。「数学ガール」での元々の評価}} + \underbrace{\frac{m-2(n+1)}{m+2i} \kumiawase{m+2i}{i+n+1}}_{\text{$s=1$ の項による補正。ちゃんと負になっている}}
\end{equation}
である。やる気のある方は、\eqref{eq:circular-randomwalk-29}からさらにStirling の評価式を用いて、「数学ガール」の評価式が改善されるかどうかチャレンジしていただきたい。

■ 無限性による微妙な点の注意

さて、最後に、本記事の最初の方で触れた無限級数の問題について述べておく。この問題では期待値は本来無限級数なので、その取り扱いがいい加減だと知らないところで矛盾が発生していて誤った結果が出てしまっていることがありうる。

例えば式\eqref{eq:circular-randomwalk-1}〜\eqref{eq:circular-randomwalk-7}は元々\eqref{eq:circular-randomwalk-17}の両辺に $n+1$ をかけ、
\begin{equation}
\label{eq:circular-randomwalk-40}
\sum_{n=1}^{\infty} na_{n} = K
\end{equation}
等の関係を背景にして、$n$ について無限和をとることにより得られるものだ。そしてここでは期待値に関する線型性 $E(X+1) = E(X) + 1$ を前提に
\[ \sum_{n=1}^{\infty} (n+1)a_{n} = K+1 \]
といった関係がなりたつとしているわけだが、これと\eqref{eq:circular-randomwalk-40}を見比べると
\begin{equation}
\label{eq:circular-randomwalk-41}
\sum_{n=1}^{\infty} a_{n} = 1
\end{equation}
でなければならない。つまり「頂点 $2$ から出発した後は、いつかは必ず $1$ に辿り着く」、もう少し正確に言えば「頂点 $2$ から出た後、一度も $1$ に戻ることなくずっと $2$ から $m$ までだけを行ったり来たりするだけの確率は、限りなく $0$ に近づく」ということがなりたっていなければならないわけで、\eqref{eq:circular-randomwalk-41}が確認できないうちは\eqref{eq:circular-randomwalk-1}〜\eqref{eq:circular-randomwalk-7}のような立式はできないわけだ。

ランダムウォークについて web で検索すると、取り上げられている題材が「再帰性」（いつかは出発地点に戻ってくる、と言えるかどうか）ばかりなのが少々食傷気味で、当初そうなる理由は「あまり予備知識を必要とせず、適度な計算量で人間の興味に訴える題材としてうってつけのものがそれ以外にほとんどない」ということだろう、と思っていた。しかし、もちろんそれもあるだろうにしろ、それ以外にもこうやって「期待値の線型性（※）に関する素朴な想定がなりたつかどうか」という重要なポイントに関わる話だった、ということに改めて気づいた（そんなことは、やはり確率論に強い方にとっては当たり前すぎるほど当たり前の話だったと思いますが）。（※話の流れ上「期待値の線型性」と書きましたが、むしろ「定数の期待値がその定数と一致するか」というポイントの方が本質的ですね）

巷間に膾炙している文書によると、普通の（無限直線や無限平面、無限 $d$ 次元格子の）ランダムウォークでの再帰確率は、$d=1,2$ では $1$ なのに $d \geqq 3$ では $1$ 未満ということなので、\eqref{eq:circular-randomwalk-41}も決して自明ではない。本記事の問題は「$1$ 次元の」円環格子上のランダムウォークだったから\eqref{eq:circular-randomwalk-41}が言えたわけだが、高次元に何らかの適切な拡張を行った場合、そうでない可能性も十分ありうる、というわけだ。