Legendre 多項式で表される確率 – 五次元世界の冒険

$\newcommand{\floor}[1]{\lfloor #1 \rfloor}
\newcommand{\Bfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor}$
だいぶ以前の話だが、「サイコロを $n$ 個振るときに、1 の目と 6 の目が同数だけ出る確率」について考えたとき、ちょっと面白い非自明な結果が導けたことがある。この確率を $p_{n}$ とすると、実は Legendre 多項式 $P_{n}(x)$ によって
\begin{equation}
\label{eq:legendre}
p_{n} = \frac{1}{\sqrt{3}^{n}} P_{n}
\biggl(\frac{2}{\sqrt{3}}\biggr)
\end{equation}
と表せるのだ。（Legendre 多項式は規格化の選び方で定数倍の違いがありうるが、ここでは
\[ P_{n}(x) = \frac{1}{2^{n}n!} \frac{d^{n}}{dx^{n}}
\bigl\{(x^{2}-1)^{n}\bigr\} \]
で定義され、$P_{n}(1)=1$ で規格化されているものとする）

この式、導いたはいいが結果（と、それをちょっと拡張した式）しかメモっていなかったため、この度久々に過程を再現しようとしてかなり手こずってしまった。何となく、それほど高度な変形をしたわけではなかった感覚が残っているので、当時の私はおそらく「その気になれば再現は難しくないはず」と軽く考えて途中の計算を処分してしまったらしい。ところがいざ取り掛ってみると苦心惨憺。「拡張した式」を手がかりにして、多少は扱いやすい等価な関係式に帰着する所までは行けたのだが、そこから先がにっちもさっちも進まなくなり、最後に「泥臭いしこれまでの計算の感触からしてうまく行く見込みは乏しそうな手だけれども、もうこれくらいしか思いつく手段がない」という方針をダメ元で試してみたところ、思いがけずすんなり計算が進んでやっとこさ示すことに成功した、という有様だった。いやはや、結果だけでもメモっておいてよかった。さもなかったら、（私にとっては）永久に失われた式になってしまった所だった（笑）。

以下では、このような確率を考えようと思ったきっかけと、どのようにしてこのような表式に至ったのか、そしてこの結果からのちょっとした考察等、\eqref{eq:legendre}にまつわることを色々と書いていきたい。

さて、\eqref{eq:legendre}を見てまず気にかかるのは $\sqrt{3}$ なんてものが現れていることだろう。「無理数が出てくるなんておかしくない？$p_{n}$ って明らかに有理数にしかなりようがないよね？」というのが第一感ではないだろうか。それはもっともな感覚だが、今の場合実際に計算してみると $\sqrt{3}$ はうまく打ち消し合ってくれる。$P_{n}(x)$ は、$n$ が偶数なら偶数次の項のみ、奇数なら奇数次の項のみを持つ多項式なので、先頭の $\dfrac{1}{\sqrt{3}^{n}}$ と合わせてそのようになるのだ。つまり、\eqref{eq:legendre}の右辺は一見無理数になりそうな形だが、それは見かけだけで、実際には必ず有理数に収まる式なのである。

$p_{n}$ という確率を考えたきっかけは、当時友人たちと遊びに集まったときに、一人が持ってきたゲームだった。これは様々な成功判定をサイコロで行い、状況によって決まる個数のサイコロを各プレイヤーが振ることになっていた。基本的には出目の合計が大きいほど有利なのだが、特別ルールとして「1 の目が出たら合計値に関わらず失敗」というルールがあった。それだけだと、サイコロの個数が増えると加速度的に自動失敗しやすくなってしまうので、救済措置として「6 の目が出ていれば、その個数分だけ 1 の目の自動失敗を打ち消せる」というルールも備わっていた。

例えば、出目が「2,5,3」なら特別ルールは発動せず単に「合計が 10」という結果になる。「1,5,5」なら合計は 11 だが 1 の目が出ているので結果は「失敗」。「1,6,2」なら 1 の目が出ているが 6 の目も出ているので自動失敗は打ち消され、「合計 9」として扱われる。「1,1,3,6」の場合は、6 の目が 1 個しか出ていないので 1 の目の自動失敗を 1 個しか打ち消せず、「失敗」という結果になる。

さて、しばらくこのゲームで遊んでみると、どうもこの救済措置が期待したほどは働いていないような感じを受けた。振るサイコロの個数が増えると、1 の目が出やすくなる代わりに 6 の目も同じだけ出やすくなるので、事前の予想ではそれらの効果は相殺して単純に「出目の合計が大きくなりやすくなって有利になる」という傾向がだいたいそのまま出てくるだろう、と踏んでいた。ところが実際にある程度試してみた感じでは、その期待よりも自動失敗がしょっちゅう起きる感じで、サイコロの個数の増加が単純に有利さに繋がってくれていない感じが拭えなかった。

そこで私はこのことを確かめるべく、「6 の目が 1 の目を打ち消して自動失敗を免れる確率を、サイコロの個数 $n$ の式として求めてみよう」と考えた。自動失敗を免れるのは「$\text{1 の目の個数} \leqq \text{6 の目の個数}$」の時だが、この確率を直接求めようとすると適合する状態数が多くて大変なので、ちょっと工夫しよう。

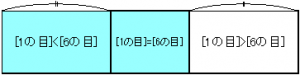
起こり得る結果は
– $\text{[1 の目の個数]} < \text{[6 の目の個数]}$
– $\text{[1 の目の個数]} > \text{[6 の目の個数]}$
– $\text{[1 の目の個数]} = \text{[6 の目の個数]}$
のいずれかだ。このうち、1 つ目と 2 つ目の確率は 1 の目と 6 の目の対等性によって等しくなる。図解すると次の図のようになっている。

図の横幅全体が全確率 $1$ だ。したがって、上記のリストの 3 つ目の確率（図の中央）を $p_{n}$ とおけば、1 つ目と 2 つ目の確率（図の左右）は共に $\dfrac{1-p_{n}}{2}$ となる。求める確率は図の水色の部分だから、
\[ \dfrac{1-p_{n}}{2} + p_{n} = \frac{1+p_{n}}{2} \]
となる。つまり、$p_{n}$ さえ求まれば
\[ \text{自動失敗を免れる確率} = \text{「$\text{1 の目の個数} \leqq \text{6 の目の個数}$」の確率} = \frac{1+p_{n}}{2} \]
として目的の確率がわかる。というわけで、目的は $p_{n}$ を求めることに帰着された。

まず、小さな $n$ に対して具体的に計算してみよう。$p_{1}$ は「サイコロを $1$ 個振るとき、1 の目も 6 の目も出ない確率」だから $p_{1}=\dfrac{4}{6} = \dfrac{2}{3}$ である。また、$p_{2}$ は「サイコロを $2$ 個振るとき、1 と 6 の目が 1 つも出ないか、1 つずつ出る確率」なので $p_{2} = \Bigl( \dfrac{4}{6} \Bigr)^{2} + 2 \times \dfrac{1}{6} \times \dfrac{1}{6} = \dfrac{1}{2}$ となる（「$2 \times$」の部分は、$2$ 個のサイコロのうちどちらが 1 の目でどちらが 6 の目を出すかが $2$ 通りあることから来る）。

$p_{3}$ は「サイコロを $3$ 個振るとき、1 と 6 の目が 1 つも出ないか、1 つずつ出る確率」となるから、$p_{3} = \Bigl( \dfrac{4}{6} \Bigr)^{3} + 3 \cdot 2 \times \dfrac{1}{6} \times \dfrac{1}{6} \times \dfrac{4}{6} = \dfrac{11}{27}$ だ（「$3 \cdot 2 \times$」の部分は、「$3$ 個のサイコロのうち、どの $1$ 個が 1 の目を出し、残りの $2$ 個のうちどちらが 6 の目を出すか」が何通りあるかを算出している）。

一般の $n$ の場合も、同様に考えれば立式できる。1 と 6 の目が共に $k$ 個ずつ出る場合を考えよう。$n$ 個のサイコロのうち、どの $k$ 個とどの $k$ 個が 1 と 6 の目を出すかは $\dfrac{n!}{(k!)^{2}(n-2k)!}$ 通りあって、そのどの場合の確率も $\Bigl(\dfrac{1}{6}\Bigr)^{k} \Bigl(\dfrac{1}{6}\Bigr)^{k} \Bigl(\dfrac{4}{6}\Bigr)^{n-2k} = \dfrac{4^{n-2k}}{6^{n}}$ である。

また、ありうる $k$ の値の範囲は $0 \leqq k \leqq \Bigl\lfloor \dfrac{n}{2} \Bigr\rfloor$ である。ここで、$\floor{a}$ は $a$ 以下の最大の整数を表す。日本の中学・高校数学では $[a]$ と書いてガウス記号というもっともらしい名前で呼ばれることが多い記号だが、海外では余り使われないようなので、ここでは世界標準に合わせた表記にしておく。

よって $p_{n}$ は
\begin{equation}
\label{eq:pn_bysum}
p_{n} = \sum_{k=0}^{\floor{\frac{n}{2}}} \frac{n!}{(k!)^{2}(n-2k)!}
\frac{4^{n-2k}}{6^{n}} = \frac{1}{6^{n}} \sum_{k=0}^{\floor{\frac{n}{2}}}
\frac{n!}{(k!)^{2}(n-2k)!} 4^{n-2k}
\end{equation}
と表される。

\eqref{eq:pn_bysum}を使って、元々考えていた「自動失敗を免れる確率」$\dfrac{1+p_{n}}{2}$ を $0 \leqq n \leqq 7$ の範囲で求めてみると、次のような表になる。
\[
\renewcommand{\arraystretch}{1.5}
\begin{array}{c|cr}
n & \text{確率} & \% \\
\hline
0 & 1 & 100 \\
1 & \dfrac{5}{6} & 83 \\
2 & \dfrac{3}{4} & 75 \\
3 & \dfrac{19}{27} & 70 \\
4 & \dfrac{875}{1296} & 68 \\
5 & \dfrac{425}{648} & 66 \\
6 & \dfrac{14973}{23328} & 64 \\
7 & \dfrac{154581}{244944} & 63
\end{array}
\]
確かに、この範囲では確率が徐々に減っている。振るサイコロが増えるほど、自動失敗に関しては不利になっているわけだ！$5$ 個以上振ると、$3$ 回に $1$ 回は出目の合計と無関係に失敗してしまう。これではおいそれとサイコロを振るわけにはいかない。

では、さらに $n$ が増えるとどうなるか。このまま単調減少を続けるのか、それともどこかで盛り返すのか。できれば、$n \to \infty$ の時の漸近的な挙動が解ると嬉しい。それには、\eqref{eq:pn_bysum}のような和による表現ではなく、$p_{n}$ を直接表す閉じた表現が望ましい。こうして、私は\eqref{eq:pn_bysum}の右辺の和を整理することを目指し始めた。

ここから先、私がどのように考えて\eqref{eq:legendre}に至ったのか、詳しいことは実はよく覚えていない。が、推測を交えて述べると、だいたい次のような経過だったのではないかと思われる。なお、以下では簡単のため $\Bigl\lfloor\dfrac{n}{2}\Bigr\rfloor$ を $N$ と略記する。

まず、\eqref{eq:pn_bysum}に現れる形を文字式に一般化した
\begin{equation}
\label{eq:34-1}
\sum_{k=0}^{N} \frac{n!}{(k!)^{2}(n-2k)!} x^{n-2k}
\end{equation}
という式に着目する。これは、多項定理
\[ (x+y+z)^{n} = \sum_{a+b+c=n} \frac{n!}{a!b!c!}x^{a}y^{b}z^{c} \]
の右辺の和から、$b=c$ であるような項だけを抜粋した形に一致している（$y=z=1$ とすれば）。そこで、「\eqref{eq:pn_bysum}の和が閉じた形に整理できるとしたら、『何かの $n$ 乗』という形がメインとなるのではないか」と推測される。

また、\eqref{eq:34-1}の $x$ のベキ乗の指数 $n-2k$ は $n, n-2, n-4,\dotsc$ と「$n$ からひとつおきに減っていったような数」が並ぶ。ベキ乗の指数がそのようになっている式で、「何かの $n$ 乗」というものが関わっている式というと、ひとつ思い当たるのが Legendre 多項式だ。

そこから、「$p_{n}$ は Legendre 多項式を使うとうまく表せたりするのではないか？」というアイディアが浮かんでくる。もちろん、この段階ではまだ極めて根拠薄弱な「思いつき」レベルの話でしかないが、当時の私はダメ元くらいの軽い気持ちでひとまずこのアイディアを試したのだと思う。

Legendre 多項式は、$(x^{2}-1)^{n}$ を二項定理でバラしてから $n$ 階微分すると、次のような形に書ける。
\begin{align}
\label{eq:34-2}
P_{n}(x) &= \frac{1}{2^{n}} \sum_{l=0}^{N}
\frac{(-1)^{l}(2n-2l)!}{l!(n-l)!(n-2l)!} x^{n-2l} \\
\label{eq:34-3}
&= \sum_{l=0}^{N} \frac{(-1)^{l}(2n-2l-1)!!}{2^{l}l!(n-2l)!} x^{n-2l}
\end{align}
これを見ると、\eqref{eq:34-1}との相性は案外よさそうに思える。和の範囲も $x$ のベキ指数も同じで、分母に現れる $l!(n-2l)!$ という形も共通だ。何とかして係数を合わせる因子をうまく調達できれば、$p_{n}$ は実際に Legendre 多項式を利用して表せてしまうかもしれない。

次の一手だが、私はどうやら割と強引に次のように考えたらしい。「\eqref{eq:34-1}の各項をどう加工すると\eqref{eq:34-2}や\eqref{eq:34-3}の形にもっと近づけられるだろうか？特に、\eqref{eq:34-1}の分母で $k!$ が $2$ 乗されているのが一番大きい障害になりそうだから、これを優先して解消したい。となると、二項定理で出てくる形の $\dfrac{k!}{l!(k-l)!} x^{2(k-l)} (-1)^{l}$ って割と有望じゃないだろうか？これをかけると
\[ \frac{n!}{(k!)^{2}(n-2k)!} x^{n-2k} \times \frac{k!}{l!(k-l)!} x^{2(k-l)} (-1)^{l} = \frac{n!(-1)^{l}}{l!(k-l)!k!(n-2k!)} x^{n-2l} \]
で、\eqref{eq:34-2}にだいぶ近づく。んじゃまあひとまず、\eqref{eq:34-1}をちょっとアレンジした
\begin{equation}
\label{eq:34-4}
\sum_{k=0}^{N} \frac{n!}{(k!)^{2}(n-2k)!} x^{n-2k} (x^{2}-1)^{k}
\end{equation}
という和でも考えてみて、これが $P_{n}(x)$ とどれくらい近くてどれくらい遠いか調べてみるか」

「どうやら…らしい」などというはなはだ頼りない話で申し訳ないが、上の方でも書いた通り、この辺りの詳細な発想は完全に記憶の彼方なのだ。自分でも「こんなにも見込みの薄そうな試行錯誤に、果たして乗り出そうという気になるだろうか？」と疑問に思うくらい適当な考えであることは否めない。だが、書き残してあった結果の式から逆算して、最終的に正しいとわかった式が\eqref{eq:34-4}に近い形なので、今となっては「当時はこう考えた」とでも思わないと\eqref{eq:34-4}が出てくる流れが思いつけない。本当かどうか定かではないが、とりあえずここではこういう流れだったとして話を進める。

小さい $n$ に対して\eqref{eq:34-4}を具体的に計算して、$P_{n}(x)$ と比べてみると、次のようになる。

$n=0, 1$ のとき: 計算過程は省略、$P_{0}(x)=1$, $P_{1}(x)=x$ と一致。

$n=2$ のとき: $N=1$ なので、
\begin{align*}
\eqref{eq:34-4} &= \frac{2!}{(0!)^{2}(2-0)!} x^{2-0} (x^{2}-1)^{0} +
\frac{2!}{(1!)^{2}(2-2)!} x^{2-2} (x^{2}-1)^{1} \\
&= x^{2} + 2(x^{2}-1) = 3x^{2}-2
\end{align*}
で、$P_{2}(x) = \dfrac{3x^{2}-1}{2}$ とは異なる。

$n=3$ のとき: $N=1$ なので、
\begin{align*}
\eqref{eq:34-4} &= \frac{3!}{(0!)^{2}(3-0)!} x^{3-0} (x^{2}-1)^{0} +
\frac{3!}{(1!)^{2}(3-2)!} x^{3-2} (x^{2}-1)^{1} \\
&= x^{3} + 6x(x^{2}-1) = 7x^{3}-6x
\end{align*}
で、$P_{3}(x) = \dfrac{5x^{3}-3x}{2}$ とは異なる。

このように、\eqref{eq:34-4}そのものは $P_{n}(x)$ とは一致しない。が、（やはりまったく記憶にはないのだが、こうやって後付けで推理するに）どうやら私は $n=2,3$ での計算過程から、「分母を適当な $2$ のベキで割ると合うようになるんじゃないか？元々 $P_{n}(x)$ の定義式は $2^{n}$ で割る形だし」と思いついたらしい。

つまり、$n=2,3$ の計算過程の $k=1$ の項 $2(x^{2}-1)$, $6x(x^{2}-1)$は、共に $4=2^{2}$ で割った $\dfrac{2(x^{2}-1)}{2^{2}}$, $\dfrac{6x(x^{2}-1)}{2^{2}}$ に入れ替えれば、$k=0$ の項 $x^{2}$, $x^{3}$ と足した結果は $P_{2}(x)$, $P_{3}(x)$ とぴったり合うようになる。

そのことを手がかりにして、私は「どうせダメ元でやってることだし、今度は和の分母に $2$ のベキを仕込んだ
\begin{equation}
\label{eq:34-5}
\sum_{k=0}^{N} \frac{n!}{2^{2k}(k!)^{2}(n-2k)!} x^{n-2k}
(x^{2}-1)^{k}
\end{equation}
が $P_{n}(x)$ と合うかどうか試してみよう」と考えたのだと思う。たぶん（これまた、本当にそうだったのかどうかの記憶はまったくない）。

【追記】
$(x^{2}-1)^{n}$ を微分するとき、$(x-1)^{n}\cdot (x+1)^{n}$ と積の形にして Leibniz rule を使う方を選べば
\begin{align*}
P_{n}(x) &= \frac{1}{n! 2^{n}} \sum_{k=0}^{n} {}_{n}C_{k}
\frac{n!}{(n-k)!} (x-1)^{n-k} \cdot \frac{n!}{k!} (x+1)^{k} \\
&\fallingdotseq \frac{1}{n! 2^{n}} \sum_{k=0}^{N} {}_{n}C_{k}
\frac{(n!)^{2}}{k!(n-k)!}
\bigl\{(x-1)^{n-k} (x+1)^{k} + (x+1)^{n-k} (x-1)^{k}\bigr\} \\
&= \frac{1}{2^{n}} \sum_{k=0}^{N} \bigl({}_{n}C_{k}\bigr)^{2}
\bigl\{(x-1)^{n-2k} + (x+1)^{n-2k}\bigr\} (x+1)^{k} (x-1)^{k} \\
&= \frac{1}{2^{n-1}} \sum_{k=0}^{N} \bigl({}_{n}C_{k}\bigr)^{2} \sum_{l=0}^{\floor{\frac{n-2k}{2}}} {}_{n-2k}C_{2l}
x^{n-2k-2l} (x^{2}-1)^{k}
\end{align*}
となって、この方が\eqref{eq:34-2}や\eqref{eq:34-3}より\eqref{eq:34-5}に近い形になる（※ ２行目で「$\fallingdotseq$」となっているのは、これだと $n$ が偶数のとき $k=N=\dfrac{n}{2}$ の項を余分に足してしまっているから）。ひょっとしたら、当時の私が\eqref{eq:34-5}を思いついたのは、こちらの形をヒントとしたのかもしれない。

で、今度も小さい $n$ の値に対して実際に\eqref{eq:34-5}を求めてみると………何と、ばっちり $P_{n}(x)$ と合ってしまうのだ！

$0 \leqq n \leqq 3$ に対して\eqref{eq:34-5}が $P_{n}(x)$ と一致するのは不思議ではない。これらに対しては和は $k=1$ までの項しかなくて、「そこまでだったら合うように」\eqref{eq:34-5}を定義してみたに過ぎないからだ。ところが、$n$ を $4,5,6, \dotsc$ と増やして、和が $k \geqq 2$ の範囲に及ぶようになっても、（具体的な計算はここでは書かないが）ずっと
\begin{equation}
\label{eq:legendre2}
\sum_{k=0}^{N} \frac{n!}{2^{2k}(k!)^{2}(n-2k)!} x^{n-2k}
(x^{2}-1)^{k} = P_{n}(x)
\end{equation}
が成立し続けているのである。

これは驚くべき結果だ（少なくとも私にとっては）。これだけ多くの $n$ に対してなりたつなら、すべての $n$ に対して\eqref{eq:legendre2}がなりたつ見込みは俄然高くなった。そしてそれが証明できないかと調べてみた結果、ついに証明に成功したのだ！（………が、例によって当時の証明方針は全然覚えていない）

さて、\eqref{eq:legendre2}の証明はちょっと後回しにして、まずは「\eqref{eq:legendre2}さえ証明できれば、冒頭に挙げた\eqref{eq:legendre}を示すことは難しいことではない」ということを確認しておこう（そのことは、試行錯誤の過程で当時の私は気づいていたはず）。

まず、\eqref{eq:legendre2}の $\dfrac{1}{2^{2k}} x^{n-2k}(x^{2}-1)^{k}$ を\eqref{eq:pn_bysum}の $4^{n-2k}$ の形に結びつけることを考える。
$\dfrac{1}{2^{2k}} (x^{2}-1)^{k} = \biggl(\dfrac{\sqrt{x^{2}-1}}{2}\biggr)^{2k}$ だから、
\begin{align}
\frac{1}{2^{2k}} x^{n-2k}(x^{2}-1)^{k} &= x^{n-2k}
\biggl(\frac{2}{\sqrt{x^{2}-1}}\biggr)^{-2k} \notag\\
&=
\biggl(\frac{2x}{\sqrt{x^{2}-1}}\biggr)^{n-2k} \cdot
\biggl(\frac{\sqrt{x^{2}-1}}{2}\biggr)^{n} \notag\\
\label{eq:34-6}
\therefore \sum_{k=0}^{N} \frac{n!}{(k!)^{2}(n-2k)!} \biggl(\frac{2x}{\sqrt{x^{2}-1}}\biggr)^{n-2k} &= \biggl(\frac{2}{\sqrt{x^{2}-1}}\biggr)^{n} P_{n}(x)
\end{align}
そこで $\dfrac{2x}{\sqrt{x^{2}-1}} = 4$ となるような $x$ を求めると $x =\dfrac{2}{\sqrt{3}}$ である。これを\eqref{eq:34-6}に代入すれば
\begin{equation}
\label{eq:34-7}
\sum_{k=0}^{N} \frac{n!}{(k!)^{2}(n-2k)!} 4^{n-2k} =(2\sqrt{3})^{n} P_{n} \biggl(\frac{2}{\sqrt{3}}\biggr)
\end{equation}
で、この両辺を $6^{n}$ で割ると\eqref{eq:legendre}を得る。

（なお、今と同様の流れによって、
\begin{equation}
\label{eq:34-14}
\sum_{k=0}^{N} \frac{n!}{(k!)^{2}(n-2k)!}t^{n-2k} = \sqrt{t^{2}-4}^{n} P_{n} \biggl(\frac{t}{\sqrt{t^{2}-4}}\biggr)
\end{equation}
も示せる。これが、冒頭で述べた「メモが残っていた、少し一般化した形」である。\eqref{eq:34-14}から逆に、$P_{n}$ のカッコ内が $x$ になるように $x=\dfrac{t}{\sqrt{t^{2}-4}}$ とおいて変形を行うと\eqref{eq:legendre2}に戻る。今回私が\eqref{eq:legendre2}を復元できたのはその流れによる）

という訳で、残った仕事は\eqref{eq:legendre2}の証明だけである。

【\eqref{eq:legendre2}の証明】
\eqref{eq:legendre2}の左辺を $Q_{n}(x)$ とおく。$n=0,1$ では $Q_{n}(x)=P_{n}(x)$ が成り立っている。

Legendre 多項式 $P_{n}(x)$ は、次の漸化式をみたしている。
\begin{equation}
\label{eq:recur}
(n+1) P_{n+1}(x) – (2n+1)x P_{n}(x) + n P_{n-1}(x) = 0 \qquad (n \geqq 1)
\end{equation}
（\eqref{eq:recur}の証明は、例えば「解析概論」$\S$ 36「Legendre の球函数」を見よ）したがって、$Q_{n}(x)$ が同じ形の漸化式
\begin{equation}
\label{eq:recurQ}
(n+1) Q_{n+1}(x) – (2n+1)x Q_{n}(x) + n Q_{n-1}(x) = 0 \qquad (n \geqq 1)
\end{equation}
をみたすことを示せば、すべての $n$ に対し $Q_{n}(x)=P_{n}(x)$ であると言える。

以下 $Q_{n}(x)$ の定義式を\eqref{eq:recurQ}の左辺に代入して整理するが、結構長い計算になるので先にちょっと準備をしておこう。まず $n=2m$ のとき $ \Bigl\lfloor \dfrac{n+1}{2} \Bigr\rfloor = m$, $N=\Bfloor{\dfrac{n}{2}} = m$, $\Bfloor{\dfrac{n-1}{2}} = m-1$ で、一方 $n=2m-1$ のとき $\Bfloor{\dfrac{n+1}{2}} = m$, $N=\Bfloor{\dfrac{n}{2}} = m-1$, $\Bfloor{\dfrac{n-1}{2}}=m-1$ だから、
\begin{equation}
\label{eq:34-9}
\begin{array}{c|c|c|}
& \Bfloor{\dfrac{n+1}{2}} & \Bfloor{\dfrac{n-1}{2}} \\
\hline
\text{$n$ が偶数のとき} & N & N-1 \\
\text{$n$ が奇数のとき} & N+1 & N \\
\hline
\end{array}
\end{equation}
である。

そして\eqref{eq:recurQ}左辺の第２項までをまず取ると
\begin{align}
&\quad (n+1) Q_{n+1}(x) – (2n+1)x Q_{n}(x) \notag\\
\label{eq:34-8}
&= (n+1) \sum_{k=0}^{\floor{\frac{n+1}{2}}}
\frac{(n+1)!x^{n+1-2k}(x^{2}-1)^{k}}{2^{2k}(k!)^{2}(n+1-2k)!} – (2n+1)
\sum_{k=0}^{\floor{\frac{n}{2}}} \frac{n!
x^{n-2k+1}(x^{2}-1)^{k}}{2^{2k}(k!)^{2}(n-2k)!}
\end{align}
だが、ここで第１項と第２項の和の範囲を $0 \leqq k \leqq N$ に揃えよう。第１項の和の部分を
\[ \sum_{k=0}^{\floor{\frac{n+1}{2}}} = \sum_{k=0}^{N} + A \]
と書き直すと、\eqref{eq:34-9}によって $n$ が偶数のときは $A=0$、$n$ が奇数のときは
\begin{align*}
A &= \frac{(n+1)! x^{n+1-2(N+1)} (x^{2}-1)^{N+1}}{2^{2(N+1)} ((N+1)!)^{2} (n+1-2(N+1))!} \\
&= \frac{(2N+2)! x^{0} (x^{2}-1)^{N+1}}{2^{2(N+1)} ((N+1)!)^{2} 0!}
\qquad (\because n=2N+1) \\
&= \frac{(2N+2)!! (2N+1)!! (x^{2}-1)^{N+1}}{2^{2(N+1)} ((N+1)!)^{2}} \\
&= \frac{2^{N+1} (N+1)! (2N+1)!! (x^{2}-1)^{N+1}}{2^{2(N+1)}
((N+1)!)^{2}} = \frac{(2N+1)!! (x^{2}-1)^{N+1}}{2^{N+1} (N+1)!} \\
\therefore (n+1) A &= (2N+2) \times \frac{(2N+1)!!
(x^{2}-1)^{N+1}}{2^{N+1} (N+1)!} \\
&= \frac{(2N+1)!! (x^{2}-1)^{N+1}}{2^{N} N!}
\end{align*}
となる。

すると\eqref{eq:34-8}は、
\begin{equation}
\label{eq:34-10}
\eqref{eq:34-8} = (n+1) A + \sum_{k=0}^{N} \frac{n! x^{n+1-2k}
(x^{2}-1)^{k}}{2^{2k} (k!)^{2} (n+1-2k)!} \bigl\{ (n+1)^{2} – (2n+1)(n+1-2k) \bigr\}
\end{equation}
である。さらに、後の変形の都合上、\eqref{eq:34-10}右辺の $\{\}$ 内を次のよう
に変形しておく。
\begin{align*}
(n+1)^{2} – (2n+1)(n+1-2k) &= (n+1)^{2}-(2n+1)(n+1) + 2k(2n+1) \\
&= -n(n+1) + 2k(2n+1) \\
&= 4k^{2} -(n+1-2k)(n-2k)
\end{align*}

続いて、今度は\eqref{eq:recurQ}左辺の第３項の和の範囲も $0 \leqq k \leqq N$ に揃えよう。今度も
\[ \sum_{k=0}^{\floor{\frac{n-1}{2}}} = \sum_{k=0}^{N} – B \]
としたい所だが、ちょっと注意が必要になる。$n$ が奇数の時は\eqref{eq:34-9}より $B=0$ で何の問題もないのだが、$n$ が偶数の時に\eqref{eq:34-9}に従って $B$ を「$k=N$ の時の $\dfrac{(n-1)!x^{n-1-2k}(x^{2}-1)^{k}}{2^{2k}(k!)^{2}(n-1-2k)!}$ の値」としようとすると、$n=2N$ なので
\begin{equation}
\label{eq:34-12}
B = \frac{(2N-1)!x^{2N-1-2N}(x^{2}-1)^{N}}{2^{2N}(N!)^{2}(2N-1-2N)!} =
\frac{(2N-1)!x^{-1}(x^{2}-1)^{N}}{2^{2N}(N!)^{2}(-1)!}
\end{equation}
となり、分母に「$(-1)!$」という訳の解らないものが出て来てしまい破綻する（$x$ の多項式のはずなのに、$x^{-1}$ という形が解消できない形になってしまっているのもおかしい）。当たり前のことだが、
\begin{equation}
\label{eq:34-11}
\sum_{k=0}^{N-1} f(k) = \sum_{k=0}^{N} f(k) – f(N)
\end{equation}
という変形をしようと思ったら、「$f(k)$ が $k=N$ という値の代入を受け付ける式かどうか」ということを事前にチェックしておかなければならなかったのだ。上の破綻はその当然の義務を怠っていたために起きた不合理である。

そこで、$f(k)$ を予め次のように変形しよう。
\begin{align*}
f(k) &= \frac{(n-1)!x^{n-1-2k}(x^{2}-1)^{k}}{2^{2k}(k!)^{2}(n-1-2k)!} \\
&= \frac{(n-1)!x^{n-1-2k}(x^{2}-1)^{k}(n-2k)}{2^{2k}(k!)^{2}(n-2k)!}
\end{align*}
この変形は、$n$ の偶奇によらず $0 \leqq k \leqq \Bfloor{\dfrac{n-1}{2}}$ のすべての $k$ に対し正しいのはもちろん、最右辺は $n$ が偶数のときに $k=N$ を代入することも可能な形になっている。よって、$f(k)$ をこの形にした上でなら、$n$ が偶数の時に\eqref{eq:34-11}を使うことができ、
\[ B = f(N) =
\frac{(2N-1)!x^{2N-1-2N}(x^{2}-1)^{N}(2N-2N)}{2^{2N}(N!)^{2}(2N-2N)!} = 0\]
となる。つまり、$n$ の偶奇によらず $B=0$ となる、とわかった。

これは要するに、$\dfrac{1}{(-1)!}$ という不合理な形を、形式的に
\[ \frac{1}{(-1)!} = \frac{0\times 1}{0\times (-1)!} = \frac{0}{0!} = 0 \]
と解釈・変形していることに相当する。こう考えると\eqref{eq:34-12}と $B=0$ に整合性があることもわかるだろう。以下でも、その解釈を採用する。

すると
\begin{align}
\text{\eqref{eq:recurQ}左辺} &= (n+1) A + \sum_{k=0}^{N} \frac{n! x^{n+1-2k}
(x^{2}-1)^{k}}{2^{2k} (k!)^{2} (n+1-2k)!} \bigl\{4k^{2} -(n+1-2k)(n-2k)\bigr\} \notag\\
&\qquad\qquad\qquad\qquad + n \sum_{k=0}^{N}
\frac{(n-1)!
x^{n-1-2k}(x^{2}-1)^{k}}{2^{2k} (k!)^{2}
(n-1-2k)!} \notag\\
&= (n+1)A + \sum_{k=0}^{N}
\frac{n! x^{n-1-2k} (x^{2}-1)^{k}}{2^{2k}
(k!)^{2} (n+1-2k)!}
\begin{aligned}[t]
\bigl\{ &\bigl( 4k^{2}-(n+1-2k)(n-2k) \bigr)x^{2} \\
&\qquad + (n+1-2k)(n-2k) \bigr\}
\end{aligned} \notag\\
&= (n+1)A + \sum_{k=0}^{N}
\frac{n! x^{n-1-2k} (x^{2}-1)^{k}}{2^{2k}
(k!)^{2} (n+1-2k)!} \bigl\{ 4k^{2}x^{2} -(n+1-2k)(n-2k)(x^{2}-1) \bigr\} \notag\\
&= (n+1)A + \underbrace{\sum_{k=0}^{N} \frac{4k^{2} n! x^{n+1-2k}
(x^{2}-1)^{k}}{2^{2k} (k!)^{2} (n+1-2k)!}}_{\text{$k=1$ からの和でも同じ}} – \sum_{k=0}^{N} \frac{n! x^{n-1-2k}
(x^{2}-1)^{k+1}}{2^{2k}(k!)^{2}(n-1-2k)!} \notag\\
&= (n+1)A + \sum_{k=1}^{N} \frac{n! x^{n+1-2k}(x^{2}-1)^{k}}{2^{2(k-1)} \bigl\{ (k-1)! \bigr\}^{2} (n+1-2k)!} – \sum_{k=0}^{N} \frac{n!
x^{n-1-2k} (x^{2}-1)^{k+1}}{2^{2k}(k!)^{2}(n-1-2k)!} \notag\\
&= (n+1)A + \sum_{k=0}^{N-1} \frac{n! x^{n-1-2k}(x^{2}-1)^{k+1}}{2^{2k}
(k!)^{2} (n-1-2k)!} – \sum_{k=0}^{N} \frac{n!
x^{n-1-2k} (x^{2}-1)^{k+1}}{2^{2k}(k!)^{2}(n-1-2k)!} \notag\\
\label{eq:34-13}
&= (n+1)A – \underbrace{\frac{n! x^{n-1-2N}(x^{2}-1)^{N+1}}{2^{2N}
(N!)^{2} (n-1-2N)!}}_{\text{$C$ とする}}
\end{align}
となる。（なお、最後から３行目と２行目の１つ目の $\sum$ は $N=0$ の時は $0$ と見なす。最終行は $N=0$ の場合も含めて使える形になっている）

ここで、$n$ が偶数の時は $n=2N$ で
\[ C = \frac{(2N)! x^{-1}(x^{2}-1)^{N+1}}{2^{2N} (N!)^{2} (-1)!} = 0 \]
だから $\eqref{eq:34-13} = (n+1)A – C = (n+1) \times 0 – 0 = 0$ となる。また、$n$ が奇数の時は $n=2N+1$ で
\begin{align*}
C &= \frac{(2N+1)! x^{0} (x^{2}-1)^{N+1}}{2^{2N} (N!)^{2}
0!}
= \frac{(2N+1)!! (2N)!! (x^{2}-1)^{N+1}}{2^{2N} (N!)^{2}} \\
&=\frac{(2N+1)!! 2^{N} N! (x^{2}-1)^{N+1}}{2^{2N} (N!)^{2}}
= \frac{(2N+1)!! (x^{2}-1)^{N+1}}{2^{N} N!}
\end{align*}
なので、
\[ \eqref{eq:34-13} = (n+1)A – C = \frac{(2N+1)!! (x^{2}-1)^{N+1}}{2^{N} N!} – \frac{(2N+1)!! (x^{2}-1)^{N+1}}{2^{N} N!} = 0 \]
でピタリ $0$ となる。

以上で\eqref{eq:recurQ}は証明された！ $\square$

冒頭でも書いたが、最近になってのこの再証明にはさんざん手こずらされた。当初は\eqref{eq:34-14}を直接証明しようとして失敗。そこで\eqref{eq:34-14}から逆算して\eqref{eq:legendre2}を出して「ルートが解消したからこれならだいぶ示しやすくなったはず」とこちらを目標に据えることにした。しかし和の式を色々いじってみるのは、ずいぶん粘ってみたけれど結局ダメで、では、というわけで Legendre 多項式の定義の１つである「自分より低次の多項式との積の、$-1 \leqq x \leqq 1$ での定積分が $0$」を示そうとしてやはり失敗。もう半分投げやりで\eqref{eq:recurQ}を示そうとしてみてやっとのことで成功、という流れだった。

得られた結果から、以下のようなことを考えてみた。いずれも「思いつき」レベルの話に過ぎないので、これらを発展させてくれる方がいれば歓迎である。

まず第一に、Legendre 多項式と言えば誰もが思い出すのが軸対称性である。そこで、確率の意味づけを巧妙に利用し、$p_{n}$ を軸対称性と結びつけて\eqref{eq:legendre}を直接導くアクロバティックな解法というのは存在しないだろうか？普通 Legendre 多項式が軸対称性と関連するときは $P_{n}(\cos \theta)$ という形をとり、引数 $x=\cos\theta$ が $\lvert x \rvert \leqq 1$ の範囲に限られてしまうから、$\dfrac{2}{\sqrt{3}}>1$ となっている\eqref{eq:legendre}と関連付けるのは一見無理そうにも思える。だが、岩波公式 III $\S$ 32 (iii) 辺りを見ると、$P_{n}(x)$ に $\cosh$ が代入されている場合も何やら意味ありげな等式が成立するようなので、軸対称性が $P_{n}(\cosh \theta)$ の形で関わってくる文脈もありうるのではないか。だとしたら、\eqref{eq:legendre}を軸対称性から導く方法も、ないとは言い切れない。

第二に、\eqref{eq:legendre}および\eqref{eq:recur}から
\begin{equation}
\label{eq:34-15}
(n+1)p_{n+1} – \frac{2(2n+1)}{3} p_{n} + \frac{n}{3} p_{n-1} =0
\end{equation}
の成立がわかるが、この漸化式を $p_{n}$ の確率としての意味から直接導くことはできないだろうか？もし\eqref{eq:34-15}が直接導けるなら、そこから逆に\eqref{eq:legendre}を導くということも可能になる。

それから、\eqref{eq:legendre2}が正しいことは漸化式\eqref{eq:recurQ}によって一応わかるのだが、この証明では「なぜ、\eqref{eq:legendre2}みたいな不思議な等式がなりたつのか？」の本質的な理由がさっぱりわかった気にならない。\eqref{eq:legendre2}はいかにもいわくありげな形をしているので、おそらく何かちゃんとした面白い背景があって、漸化式（数学的帰納法）によるのではなくもっと直接的に等式の成立を示せる方法があるのではないか、と思っているのだが…。

【追記】前からお世話になっている、私よりはるかに優秀な方から「Leibniz rule の多項定理版で直接示せる」とご教示頂きました。確かに…！言われてみれば当然そういった方向性へ考察を進めてみるべき状況です。自分の見通しのなさに愕然としますね！

実際、Wolfram Alpha に\eqref{eq:legendre2}の左辺をぶち込むと、シレッと Legendre 多項式 $P_{n}(x)$ だよ、という答を返してくれるので、直接的な式変形で示す方法がある気配は濃厚にする。\eqref{eq:pn_bysum}の和の式を Wolfram Alpha に放り込むと超幾何関数による閉じた（？）形の答が返ってくることからして、\eqref{eq:pn_bysum}や\eqref{eq:34-14}の類の和の形に対しては、どうやら超幾何関数の恒等式が何かある雰囲気なのだが…（おそらく、Wolfram Alpha にはその恒等式がインプットされていて、こちらが与えた式がそれに適用できる形になっている、ということを割り出しているのだろう）。

なお、\eqref{eq:legendre}を求める動機となった「$p_{n}$ の $n \to \infty$ での漸近形」だが、結局よくわからなかった。$x$ を固定したときの $P_{n}(x)$ の $n \to \infty$ での漸近形は、$x=\cos\theta$ の場合は岩波公式 III に載っているのだが、$x>1$ の場合は一体どうなっているのか…（$P_{n}(x)$ を複素積分表示して鞍点法とか使わないとダメ？）とりあえず、漸化式\eqref{eq:34-15}からの解析で、「$n \to \infty$ のとき $p_{n}$ が極限値を持つならそれは $0$ しかありえない」という所までは調べたので、本当に収束するのだとすれば元々の「自動失敗を免れる確率」の極限値は $\dfrac{1}{2}$ ということになるわけだが…。

【2015, 4/1 追記】
$p_{n}$ は $n \to \infty$ のとき $0$ に収束することがわかった。次々回の記事参照。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル