\(\newcommand{\abs}[1]{\lvert #1 \rvert}\)
みなさんお馴染みの \(\varepsilon\)—\(\delta\) 論法。
\begin{equation}
\label{eq:epsilon-delta-1}
\text{どんなに小さな正の数$\varepsilon$に対しても、正の数$\delta$を適切に選べば、$0<\abs{x-a}<\delta$であるすべての$x$に対し$\abs{f(x)-b}<\varepsilon$がなりたつ}
\end{equation}
極限概念を精密化するためには必要不可欠な論法だ。「解りにくい論法」の代名詞的存在として槍玉に挙げられることも多いが、一度理解できてしまえば別にこれと言って難しくはない、ということもよくご存知だろう。度々接するうちにすっかりその用法に慣れ、自分でも数々の成果を導くくらいに習熟した、という方も多いはずだ。
だが人よ、忘るることなかれ。飼い慣らしたと思い込んでいた猛獣は、実は密かに爪を研ぎ、牙を剥く機会を眈々と狙っている(かもしれない)のだ!
■ 論理式による \(\varepsilon\)–\(\delta\) 論法の表現
\(\varepsilon\)–\(\delta\) 論法を学習した方なら、次の形はよくご存知のはずだ。
\begin{equation}
\label{eq:epsilon-delta-3}
\forall \varepsilon>0, \exists \delta>0, 0 < \abs{x – a} < \delta \implies \abs{f(x) – b} < \varepsilon
\end{equation}
言うまでもなくこれは\eqref{eq:epsilon-delta-1}を論理記号を使って書き換えたものだが、初めて\eqref{eq:epsilon-delta-3}を見たとき「\eqref{eq:epsilon-delta-1}の『どんなに小さな』の『小さな』がどこかに行ってしまって、ただの『どんな(\(\forall\))』にすり替わってしまった」ことが引っかからなかっただろうか。\eqref{eq:epsilon-delta-1}では \(\varepsilon\) が極めて微小で、それをより小さくしていく方向のことしか考えていないのに、\eqref{eq:epsilon-delta-3}の「\(\forall \varepsilon>0\)」だとそんなことはお構いなしに、\(\varepsilon\) がとてつもなく大きい場合まで含んでしまっている。そのせいで\eqref{eq:epsilon-delta-1}との同値性が崩れてしまう恐れはないのだろうか——ということは、最初気になった人もいたはずだ。
\(\varepsilon\)—\(\delta\) 論法を修めた人は、これに対する答は当然持っているだろう。\eqref{eq:epsilon-delta-3}の意味を吟味してみれば、結局この形でも「どんなに小さな」とした場合と同じ意味になる。このことが理解できた人は、その後の経験で\eqref{eq:epsilon-delta-3}と類似の構造の論理式を見た場合でも、「これは \(\forall\) が付いていても、実質的には \(\varepsilon\) が微小で、より小さくなっていく場合のみを考えるのと同じことだ」ということは難なく理解できていったことと思う。
\(\varepsilon\)—\(\delta\) 論法に対して、個人的にちょっと感じている不満点は、元々の直感的極限概念
\begin{equation}
\label{eq:epsilon-delta-2}
\text{$x$が$a$に限りなく近づくとき、$f(x)$が$b$に限りなく近づく}
\end{equation}
は動的なビジョンが前面に出ている(と言うか、動的なビジョンのみで構成されていると言っていい)のに対し、\eqref{eq:epsilon-delta-3}の形になるとそのようなビジョンは影を潜め、意味づけを読み解くことでしかその姿を現さないことだ。\(\varepsilon\)–\(\delta\) 論法を学習済みの人にとっては、両者の等価性が頭の中に克明に刻まれていて、\eqref{eq:epsilon-delta-3}の形を見ただけでほとんど無意識のうちに直ちに動的なイメージに翻訳・変換されてしまうので余り意識することはないと思うが、\eqref{eq:epsilon-delta-3}の形そのものにはやはり元々の\eqref{eq:epsilon-delta-2}ほどにストレートな動的概念はなく、静的(少なくとも\eqref{eq:epsilon-delta-2}に比べれば)な装いをしている。そういう意味で、\eqref{eq:epsilon-delta-3}と\eqref{eq:epsilon-delta-2}は本来は概念的に別々のものであって、そこに込められた意味を能動的に読み込み、解釈が橋渡しされることによって初めてその等価性が浮かび上がってくる…という関係にあると言っていいだろう。
■ 一般相対性理論での時空の因果構造
突如話は変わるが、一般相対性理論の基礎方程式である Einstein 方程式は非線形偏微分方程式であるため、解の構造を数学的に厳密に分析することは難しい。しかし、1960〜70年代に Hawking や Penrose らによって、非線形偏微分方程式という難物を正面から相手にしなくても、特異点定理やブラックホールの面積定理・非分裂定理といった注目すべき定理が数学的に厳密に導ける、という発見があった。その基礎になっている「時空の因果構造」の研究の中で、strongly causal という概念が出てくる。
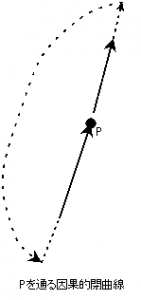 時空の因果構造は、物理法則の無矛盾性のために重要だ。未来へ進んでいく世界線が、ぐるっと回って元の時空点に戻って来てしまうようなことがあった場合、未来と過去が繋がってしまうことになる。これは要するにタイムマシンに乗って過去の自分と出会うということだが、SF 的には面白く想像力が刺激される現象である一方、物理的・数学的にはかなり困った事態を引き起こす。「親殺しのパラドックス」が端的に示す概念上の矛盾がどう解決されるのかわからないのはもちろん、未来と過去がつながってしまうと、運動方程式や物質場の時間発展の微分方程式を初期値問題として解いた場合、未来に向かって解いて行った解の値が、元の時刻に戻ってきたとき、元々与えられていた初期値と一致する保証がなくなってしまう。無矛盾性の要請のため、可能な初期配置は非常に限られたものしか許されなくなったり、場合によってはいかなる初期配置でも矛盾が生じてしまう、ということになりかねない。
時空の因果構造は、物理法則の無矛盾性のために重要だ。未来へ進んでいく世界線が、ぐるっと回って元の時空点に戻って来てしまうようなことがあった場合、未来と過去が繋がってしまうことになる。これは要するにタイムマシンに乗って過去の自分と出会うということだが、SF 的には面白く想像力が刺激される現象である一方、物理的・数学的にはかなり困った事態を引き起こす。「親殺しのパラドックス」が端的に示す概念上の矛盾がどう解決されるのかわからないのはもちろん、未来と過去がつながってしまうと、運動方程式や物質場の時間発展の微分方程式を初期値問題として解いた場合、未来に向かって解いて行った解の値が、元の時刻に戻ってきたとき、元々与えられていた初期値と一致する保証がなくなってしまう。無矛盾性の要請のため、可能な初期配置は非常に限られたものしか許されなくなったり、場合によってはいかなる初期配置でも矛盾が生じてしまう、ということになりかねない。
このような困難を避けるため、時空の因果構造を議論する場合は、通常「未来と過去がつながらない」という条件をつける。さてこの条件だが、単に「未来から過去につながる世界線(閉じた因果的曲線)が存在しない」という条件だけでは、物理的時空に対する制約としては不十分と通常見なされる(先に進む前にちょっと用語の説明をしておく。Lorentz 符号の計量があるとき、\(0\) ベクトル以外のベクトルは自分自身との内積の符号に応じて時間的・ヌル(光的)・空間的の3タイプに分かれるが、このうち時間的・ヌルの2タイプを合わせて因果的という。時空中で常に因果的なベクトルに沿った曲線が因果的曲線。別の言い方をすれば、常に(未来側の)光円錐の内側(側面も含む)に向かって進んでいく曲線が因果的曲線だ。通常の物質も光も、世界線は因果的曲線になる)。時空の性質・構造を数学的に論じる場合、現実世界でその辺に浮いているホコリ等の微小なノイズは無視して理想化された数学的モデルに基づいて議論するわけだから、実際の「ホコリ」によってモデルに微小なずれが加わっただけで破綻するような時空は、物理的には不適な範疇に入れなければならない。したがって、因果構造について考えるときは、「閉曲線に限りなく近い因果的曲線」を持つ時空も除外しなければならない。そのような曲線が存在すると、微小な「ホコリ」によるごくわずかな変化でも「実際に閉じた因果的曲線」が生じてしまうと考えられるからだ。この「閉曲線に限りなく近い因果的曲線」を持たない、ということを言い表そうとしたものが strongly causal という条件だ。
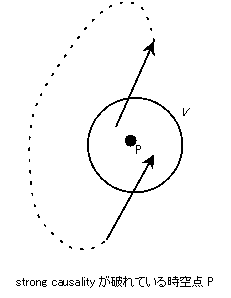 時空点 P で strong causality が破れているとは、次のことが成り立つことを言う:
時空点 P で strong causality が破れているとは、次のことが成り立つことを言う:
\begin{equation}
\label{eq:epsilon-delta-4}
\text{Pを含むどんなに小さい(開)近傍$V$を取っても、$V$の中から出て行って、再度$V$に戻ってくる因果的曲線が存在する。}
\end{equation}
そして、strong causality が破れているような時空点を持たない時空は strongly causal であるという(閉じた因果的曲線を持たないのに strongly causal でないような実例は簡単には思いつきにくく、「そんな時空は存在しないのでは?」と思う方も少なくないだろう。簡単な実例は自然さを犠牲にしないと作れないため、この分野をかじったことのない人がいきなり思いつくのは難しいが、参考文献 [1] p.197 や [2] p.193 に例が挙がっている)。※ 「strong」の語の由来は、単なる「閉じた因果的曲線が存在しない」というだけの弱い(weak)条件ではない、ということなのだろう。
さて、\eqref{eq:epsilon-delta-4}が \(\varepsilon\)—\(\delta\) であることは明白だろう。そこで、ちょっと次の問題に取り組んで頂きたい。\eqref{eq:epsilon-delta-4}を論理式を使った形に書き直すとどうなるだろうか?ちょうど、\(\varepsilon\)—\(\delta\) 論法を日本語の文として表した\eqref{eq:epsilon-delta-1}を、論理式の組み合わせで表した\eqref{eq:epsilon-delta-3}に書き直したように。「(開)近傍」や「因果的曲線」を論理式で簡潔に表現するのは難しいが、そこは無理に論理式に直さなくても構わない。考えてほしいポイントは、「\(\forall\)」と「\(\exists\)」をどのような形で使うかだ。
結果はおそらく、こんな形になったのではないだろうか。
\begin{equation}
\label{eq:epsilon-delta-5}
\forall V \owns \text{P}, \exists \lambda, \text{$\lambda$は$V$と$2$回以上交わる}
\end{equation}
ここで、\(V\) は近傍(開集合)、\(\lambda\) は因果的曲線とする。このくらいの書き直しは、\(\varepsilon\)—\(\delta\) 論法に慣れていれば朝飯前、という感覚だろう。
ところがこれではまずいのだ。
P の近傍 \(V\) として、時空全体をとってみよう。そうすると、\(V\) と \(2\) 回以上交わる曲線などあるはずがない。つまり、\eqref{eq:epsilon-delta-5}を strong causality の破れと定義してしまうと、破れている点など存在し得ないことになり、ありとあらゆる時空が strongly causal になってしまう、ということだ。つまり、\eqref{eq:epsilon-delta-5}では\eqref{eq:epsilon-delta-4}が表そうとしている概念を正しく表現できていないのだ。
これに対する解決策は、再度\eqref{eq:epsilon-delta-4}に戻って意味を考え直すとすぐ思いつくだろう。第2案はこうではないだろうか。
\begin{equation}
\label{eq:epsilon-delta-6}
\exists V \owns \text{P}, \exists \lambda, \text{$\lambda$は$V$と$2$回以上交わる}
\end{equation}
\(\forall\) が \(\exists\) に変わってしまったが、「閉曲線に限りなく近い因果的曲線」とは要するに「P の近傍から一旦離れたはずの因果的曲線が再度 P の近傍まで戻ってきてしまう」というものなのだから、\(\forall\) と \(\exists\) の違いは実は本質的ではない———そう考えれば\eqref{eq:epsilon-delta-6}に行き着く。
が、残念ながらその考えは誤りだ。
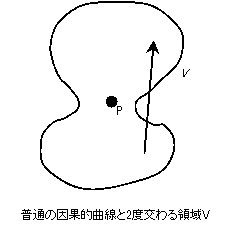 とっさに考えると十中八九\eqref{eq:epsilon-delta-6}としてしまうだろうが、今度は P の近傍 \(V\) として、図のようなひょうたん型の領域を取ってみよう。すると、ごく普通の因果的曲線が \(V\) と \(2\) 回交わってしまう。よって\eqref{eq:epsilon-delta-6}が定義だとすると、今度はありとあらゆる時空点 P で strong causality が破れていることになり、ひいては strongly causal な時空などない、ということになってしまう。やはり \(V\) については「\(V\) がどんな形をしていても…」という定式化をしないと、strong causality の破れという特殊な因果的条件を表すのは難しいわけだ。「\(\exists V\)」では失敗する所以である。(※ なお上の例で、ひょうたん型であることは本質ではなく、\(V\) の境界の一部が(滑らかな)時間的超曲面になっていれば同じことになる)
とっさに考えると十中八九\eqref{eq:epsilon-delta-6}としてしまうだろうが、今度は P の近傍 \(V\) として、図のようなひょうたん型の領域を取ってみよう。すると、ごく普通の因果的曲線が \(V\) と \(2\) 回交わってしまう。よって\eqref{eq:epsilon-delta-6}が定義だとすると、今度はありとあらゆる時空点 P で strong causality が破れていることになり、ひいては strongly causal な時空などない、ということになってしまう。やはり \(V\) については「\(V\) がどんな形をしていても…」という定式化をしないと、strong causality の破れという特殊な因果的条件を表すのは難しいわけだ。「\(\exists V\)」では失敗する所以である。(※ なお上の例で、ひょうたん型であることは本質ではなく、\(V\) の境界の一部が(滑らかな)時間的超曲面になっていれば同じことになる)
ここまで来ると、\eqref{eq:epsilon-delta-4}の正しい定式化というのが、当初思ってもみなかった手強い問題であることがわかってきたのではないだろうか。そう。すっかり自家薬籠中の物にしたとばかり思っていた \(\varepsilon\)—\(\delta\) 論法。それが突如として従順な装いをかなぐり捨て、夢にも思っていなかった難題として目の前に立ちふさがってきたのだ!
果たして、この問題はどうすれば解決できるのだろうか。改めて考えてみて頂きたい。
———腰を据えてじっくり取り組んでみると、次のことがわかってくるだろう。これは\eqref{eq:epsilon-delta-4}の「どんなに小さい」の「小さい」を無視せずにきちんと取り入れなければいけない事案なのだ、ということが。\eqref{eq:epsilon-delta-5}のように「小さい」を無視して単なる「\(\forall\)」にすると、\(V\) をどんどん大きくしていくことも許容されてしまい、そうすると大きすぎる近傍、例えば「時空全体」を \(V\) として取ることで破綻してしまうわけだ。
何ということだ。\(\varepsilon\)—\(\delta\) 論法の学習過程で「気にしなくていい瑣末な問題」という理解に達し、「解決済み」のラベルを貼って引き出しの片隅に放り込んでおいたはずの「どんなに『小さい』」問題が、こんな辺境の地(という感覚だろう、大抵の人は)で強敵として甦ってこようとは。
ではそろそろ答合わせの時間だ。一般相対論の教科書で因果構造の章を持つものや、この問題について論じている学術論文には、もちろんきちんとした正しい定式化が載っている。時空点 P で strong causality が破れている、ということは、厳密には次のように定義される。
P の近傍 \(O\) として、こういうものが存在する: \(O\) に含まれるどんな P の近傍 \(V\) に対しても、\(V\) と \(2\) 回以上交わる因果的曲線が存在する
論理記号を使って書くと
\begin{equation}
\label{eq:epsilon-delta-7}
\exists O \owns \text{P}, O \supset \forall V \owns \text{P}, \exists \lambda, \text{$\lambda$は$V$と$2$回以上交わる}
\end{equation}
となる。ただし、\(O, V\) は近傍(開集合)で、\(\lambda\) は因果的曲線である(※ 文献に実際に書いてあるのは、P で strong causality が「成立する」方の条件、つまり\eqref{eq:epsilon-delta-7}の否定が書いてあることが多いようだ。ここでは本記事の話の流れに沿って、strong causality が「破れる」条件に直して書いてある)。
つまり、考え方はこうだ。\(V\) として大きすぎる近傍を許すと破綻してしまうので、\(V\) の「大きさ」には上限をつける。その上限が \(O\) だ。P の近傍として、あらかじめ定まっている \(O\) という近傍よりも小さなすべての近傍に対して○○○がなりたつ…という形にすることで、「どんなに『小さい』」の「小さい」をきちんと定式化することができる、というわけである。そのためには、論理記号が「\(\exists O\), \(\forall V\), \(\exists \lambda\)」と立て続けに \(3\) 個も必要になるわけだ。通常 \(\varepsilon\)—\(\delta\) 論法では「\(\forall\), \(\exists\)」の順で \(2\) つで済んでいたというのに。
本記事では\eqref{eq:epsilon-delta-4}, \eqref{eq:epsilon-delta-5}, \eqref{eq:epsilon-delta-6}, \eqref{eq:epsilon-delta-7} と順を追ってきたので、\eqref{eq:epsilon-delta-7}の \(O\) の役割についての疑問はわかないだろう。しかし、途中経過抜きでいきなり\eqref{eq:epsilon-delta-7}に出くわしたら、\(O\) が何の意味を持っているのか、すぐにはわからなかったのではないだろうか。何を隠そう、私がそうだった。相当以前の話になるが、輪講で [1] を読んでいて strongly causal の概念が出てきた時、初見では「この \(O\) は一体何で出てきてるんだろう?こんなの不要で、単に\eqref{eq:epsilon-delta-5}にすればいいだけじゃないの?」としか思えなかった。結局、輪講の時点で \(O\) の意義が読み取れていた人は私も含め誰も居なかった。事情がわかったのは、結構後になってからの話である。
また、交流があったとある大学の研究室の定例セミナーで時空の因果構造がテーマになっていた回で、発表者は strongly causal(の破れ)の定義を\eqref{eq:epsilon-delta-5}にしてしまっていた。話が終わった後で発表者に「元の文献では\eqref{eq:epsilon-delta-7}の形になっていたが、なぜ\eqref{eq:epsilon-delta-5}にしたのか」と確認した所、見事に上とまったく同じ流れを辿った。(つまり「どっちでも同じことになるよ」「いやそれだと \(V\) を時空全体に取ってしまうとうまく行かない」「そうか…じゃあ\eqref{eq:epsilon-delta-6}にすればいいのでは」「ところがそれだと \(V\) をひょうたん型に取るとやっぱりだめ」「…あれ?」「つまり\eqref{eq:epsilon-delta-7}の \(O\) ってのはちゃんと意味があって、これを取っちゃうわけにはいかないんだよ」という流れ)
専門分野の1つに相対論を抱えている研究室の大学院生でさえ \(O\) の意義が読み取れず、\eqref{eq:epsilon-delta-5}が\eqref{eq:epsilon-delta-4}の正しい定式化になると思い込んでしまっていたくらいなのだから、予備知識のまったくない方にとっては、これは間違えるのが当たり前なくらいの問題だと言っていいだろう(などと色々偉そうなことを書いてしまったが、これは理論物理出身だからこそそう思うだけで、実は数学プロパーの人からすると「どんなに『小さい』」の「小さい」を考えに入れないといけない、なんてことは、その解決法も含めてありふれた話なのかもしれない。もしそうだったら、コメント欄で優しく教えてください(笑))。
「\eqref{eq:epsilon-delta-4}の正しい定式化」にこれほどの困難を来す理由は、本記事の始めの方で書いた「直感的極限概念\eqref{eq:epsilon-delta-2}と、\(\varepsilon\)—\(\delta\) 論法による精密化\eqref{eq:epsilon-delta-3}は概念上は別個の話だ」ということと、本質的な部分は共通しているのではないか、と私は思っている。概念的には別、という齟齬があるからこそ、形をなぞっただけの単なる「直訳」\eqref{eq:epsilon-delta-5}ではうまく行かず、より根源的な部分まで遡って「結果的に等価になる論理式」\eqref{eq:epsilon-delta-7}を構築しなければならなくなる———それが、今回の話のポイントだったのではないだろうか。こういうことからも、私には\eqref{eq:epsilon-delta-2}と\eqref{eq:epsilon-delta-3}の等価性は予めそれら自身のうちに封入されたものではなく、外的に後づけで付与されるものだ、と思えてしかたないのだ。
最後に、ものすごく野暮な話ながら、「\eqref{eq:epsilon-delta-2}と\eqref{eq:epsilon-delta-3}の間ではなぜ「どんなに『小さな』」の「小さな」があってもなくても同じ話になったのか」のもう少し掘り下げた説明を書いておく。本記事の前半部分では割とぼかした書き方で『\eqref{eq:epsilon-delta-3}の意味を吟味してみれば、結局この形でも「どんなに小さな」とした場合と同じ意味になる』と誤魔化しているが、そんなことをした理由は、ぼかさず書いてしまうと\eqref{eq:epsilon-delta-4}の書き換えが\eqref{eq:epsilon-delta-5}ではまずい理由がバレバレになってしまうし、\eqref{eq:epsilon-delta-7}の形に到達する上での大きなヒントになってしまうからだ。ご容赦を願いたい。自分で考える楽しみを奪われたくない方は、ここで読むのをストップしてくださいますよう。
と言っても大した話ではない。\eqref{eq:epsilon-delta-3}のうち、「\(\forall \varepsilon>0\)」を除いた残り
\begin{equation}
\label{eq:epsilon-delta-8}
\exists \delta>0, 0 < \abs{x – a} < \delta \implies \abs{f(x) – b} < \varepsilon
\end{equation}
を取り出してみると、これは「\(\varepsilon\) に対する条件としては、\(\varepsilon\) が大きいほど単調に成立しやすくなっていく」ようなものになっている。例えば\eqref{eq:epsilon-delta-8}が \(\varepsilon=1\) に対して成立するなら、\(1\) より大きい \(\varepsilon\) すべてに対しても\eqref{eq:epsilon-delta-8}の成立が自動的に保証される(\(\varepsilon=1\) の時と同じ \(\delta\) を取ればよい)。そんな風に、\eqref{eq:epsilon-delta-8}は、ある(正の)\(\varepsilon\) についてなりたつことがあったら、それよりも大きい値のすべての \(\varepsilon\) に対しなりたつ形だ。この単調性がポイントで、そのおかげで「\(\forall \varepsilon>0\), \eqref{eq:epsilon-delta-8}」という命題の真偽は、\(\varepsilon>0\) が「より小さく」なっていく場合の挙動(のみ)にかかっているわけである。
ところが\eqref{eq:epsilon-delta-5}になると、「\(\forall V\owns \text{P}\)」を除いた残り「\(V\) と \(2\) 回以上交わる因果的曲線 \(\lambda\) が存在する」には \(V\) に関する類似の単調性はない。このため、「どんなに『小さい』」の「小さい」を無視するわけにはいかなくなっている、というわけだ。
参考文献:
[1] Robert M. Wald, “General Relativity”, The University of Chicago Press, 1984
[2] S. W. Hawking and G. F. R. Ellis, “The large scale structure of space-time”, Cambridge University Press, 1973
コメントを残す