基本平行四辺形格子の面積

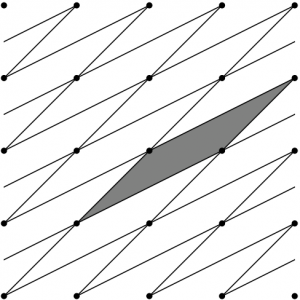
「\(xy\) 平面上で、4 つの頂点がすべて格子点の平行四辺形が、内部にも周上にも格子点を持たなければ面積が \(1\) になる」ことを示す。平行四辺形の面積公式 \(\lvert ad-bc \rvert\) は使わない。

仮定をみたす平行四辺形と合同（裏返さない）な平行四辺形を辺がぴったり揃うように並べて \(xy\) 平面を覆い尽くす斜め格子を作ると、どの平行四辺形についても仮定の性質がなりたつ。つまり \(xy\) 平面上のどの格子点も、それらの平行四辺形の頂点になるしかない。特に、\((0,0)\) や \((0,1)\) も頂点である。

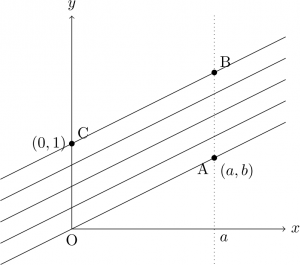
これらの格子上で、原点 O の右隣の格子点（普通は２つある。そのどちらでもよい）を \(\text{A}(a,b)\) とする（\(a\) は正の整数となる）。\((0,1)\) を C とし、平行四辺形 OABC ができるように点 Bをとる。

格子を作る直線群のうち、OA と平行なものに着目する。これらの直線上には、格子点が \(\text{OA}=\sqrt{a^{2}+b^{2}}\) 間隔で並ぶので、OA と BC の間を通るものはいずれも平行四辺形 OABC の内部にちょうど 1 つの格子点を持つ（\(\because\) これらの直線による平行四辺形 OABC の切り口の長さはいずれも OA に等しく、かつ辺 OC 上と AB 上には両端以外の格子点はない）。また、平行四辺形 OABC 内にそれら以外の格子点はない。

それらの格子点の \(x\) 座標は \(1, 2, \dots, a-1\) のいずれか。逆に、直線\(x=1, x=2, \dots, x=a-1\) 上には、平行四辺形 OABC 内に 1 つずつ格子点がある（\(\because\) これらの直線による平行四辺形 OABC の切り口の長さはちょうど\(1\) で、かつ辺 OA, BC 上には両端以外の格子点はない）。

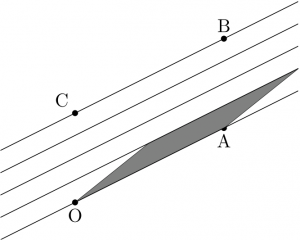
よって、OA と BC の間の直線群はちょうど \(a-1\) 本。直線群は等間隔で走っているから、これらが平行四辺形 OABC を \(a\) 等分する。よって、等分されたひとつ分の面積は
\[ \frac{\text{平行四辺形OABC}}{a} = \frac{1 \times a}{a} = 1 \]
である。なお、ここまでの議論は暗黙のうちに \(a>1\) と仮定していたが、この結果は \(a=1\) の場合も含めてなりたつ。

一方、この等分されたひとつ分の面積が元々の基本平行四辺形の面積を等積変形したものであるから、題意は示された。\(\square\)

前回書いた通り、別に自慢しようと思って書いているわけではない。成書を当たれば同じ方針のものはいくらでも出てくるだろう。実際、これはだいぶ以前の「大学への数学」で Weyl の一様分布定理の初等的な証明の紹介記事中で使われていた議論を一部取り出して修正したものに過ぎない。それに、面積公式 \(\lvert ad-bc \rvert\) を使えばもっと簡単に示せることで、面積公式は特に使用を避けるべき理由など見当たらない基本的な事実（少なくとも、高校生以上にとっては）だから、面積公式を使わないからと言ってそのことに特段意義があるわけでもない。ただ、あまり見かけない証明なので、参考のために披露しておこうと思っただけである。