\(\DeclareMathOperator{\Gal}{Gal}
\newcommand{\lnsg}{\mathrel{\vartriangleleft}}
\newcommand{\field}[1]{\mathbb{#1}}
\newcommand{\Q}{\field{Q}}
\newcommand{\K}{\field{K}}
\newcommand{\tmod}[1]{\text{mod}\; #1}
\newcommand{\zettaiti}[1]{\lvert #1 \rvert}\)
ガロア理論による方程式の可解性について理解できた私にとって、次の目標となったのは、志賀本の p.101 で、ガロアが到達した成果として挙げられていた次の話を理解することだった。
\(f(x)=0\) を有理数体 \(\Q\) 上で既約な素数 \(p\) 次の方程式とする。このとき \(f(x)=0\) が代数的に解かれるための条件は、\(f(x)\) の最小分解体 \(\K\) が、\(f(x)=0\) の解 \(\alpha_{1}, \alpha_{2}, \dots, \alpha_{p}\) の任意の \(2\) つ \(\alpha_{i}, \alpha_{j}\) を \(\Q\) に添加して得られることである: \(\K=\Q(\alpha_{i}, \alpha_{j})\)
これについてはこれまで参照してきた文書中には言及がなく、自力でもどうやったものかさっぱり見当がつかずに困っていた。ようやく割と最近になって、「ガロア論文の古典的証明」がこれに触れていることを知り、がんばって読み始めたのだが、肝心の部分に(私には)理解不能な点や、ギャップが(私にとっては)大きすぎて埋められない箇所が多く、残念ながら解決とは行かなかった(とは言え、後述する「1次式で表される群」がキーポイントになる、ということは見て取れて、それが後で結構大きく効いたので、その点は感謝したい)。
「やはり、ガロアの論文に沿って解説を進めたちゃんとした成書を買って読むしかないか…」と思っていたところ、以前も触れたある方に「体とガロア理論」藤﨑源二郎(岩波基礎数学選書、岩波書店)にその証明があると教えて頂き、先日個人的な伝手によってその本をお借りすることができた(ちょっと紛らわしいが、教えてくれた方と貸してくれた方は別人)。そこには見事な証明が書かれており、ついにその証明も理解することができた!これで一連の個人的動機に基づく学習も一段落させることができた。
【 2017,11/6 追記 】「ガロアの時代 ガロアの数学〈第2部〉数学篇」のカスタマーレビューを見ると、この本にも載っていたみたいですね。
さて、藤﨑本の理解を深めようとその証明をじっくり吟味したり、整理したりしているうちに、部分的には実質的な重複があったり、もうちょっと簡素化できそうな部分もあることがわかってきた。藤﨑本はなるべく依存性の少ない議論を可能にするために(であろう、恐らく)、証明の大半を有限群論の枠内のみで完結させており、そのため有限群論の補題をたくさん用意して証明する、という流れになっている(もちろん、それらの補題は今テーマにしている定理の証明のためだけにあるわけではなく、別の定理の証明でも利用しているようだし、補題それ自身に有限群論の成果として有用性があるので列挙されているという面も大きいのだろう)。しかし、今の我々のように「方程式の可解性をガロア理論を通じて調べる」ということを主題にしている立場からすると、その議論の一部はガロア理論の成果を利用すればすぐに出てくる、という部分もあったりするのだ。
そこで、自分の理解を整理・確認するため、そして何より自己満足のために(笑)、藤﨑本の証明を自分なりに整理・一部再構成したものを以下にまとめておくことにする。
まず、我々が証明したい主定理は以下の通りである(藤﨑本 p.249 定理 3.69)。なお、表記についてはここまでメインテキストとしてきた「ガロア理論入門ノート」に合わせたり、予備知識を必要としない形に書き直したりしている。
【定理】
\(K\) を標数 \(0\) の体とし、\(f(X)\) を \(K\) 係数、素数 \(p\) 次の既約多項式とする。\(f(X)\) の根を \(\alpha_{1}, \dots, \alpha_{p}\) とし、\(L=K(\alpha_{1}, \dots, \alpha_{p})\) を \(K\) 上の \(f(X)\) の最小分解体、方程式 \(f(X)=0\) の \(K\) に関するガロア群を \(G=\Gal(L/K)\) とする。この時、次の3つは同値。(I) \(f(X)=0\) は \(K\) に関して代数的に可解。つまり、\(G\) は可解群。
(II) \(G\) を根の添字 \(1, \dots, p\) に対する置換群と見たとき、あらかじめ根 \(\alpha_{1}, \dots, \alpha_{p}\) の番号を適当に振り直しておけば、\(G\) のどの元の作用も \(\tmod{p}\) に関する \(1\) 次式 \(ax+b\) で表される。(つまり、\(\sigma \in G\) に対して \(\sigma(x) \equiv ax+b \pmod{p} \quad (x=1,\dots, p)\) となるような整数 \(a\), \(b\) がどの \(\sigma\) に対しても取れる。なおこのとき、\(\sigma^{-1}\) が存在することから \(a \not\equiv 0 \pmod{p}\) である)
(III) \(f(X)\) の任意の(異なる)\(2\) 根 \(\alpha_{i}\), \(\alpha_{j}\) を \(K\) に添加するだけで \(L\) が得られる: \(L=K(\alpha_{i}, \alpha_{j}) \quad (i \ne j)\)
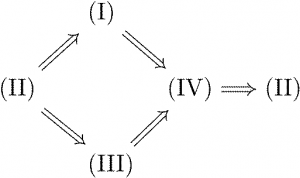
詳細に入る前に、証明の大まかな構造を概観しておく。藤﨑本の証明は「\(\text{(I)} \implies \text{(II)}\)」「\(\text{(II)} \implies \text{(III)}\)」「\(\text{(III)} \implies \text{(I)}\)」の3つを示すという構成になっているが、そのうち「\(\text{(III)} \implies \text{(I)}\)」の後半は実質上「(II) を示すことで (I) を示す」という内容になっており、また (III) から (II)(に当たること)を示す部分は途中から「\(\text{(I)} \implies \text{(II)}\)」と共通化・簡素化できる内容になっている。
また、(I)(II)(III) のうち、形式上最も強いのは (II) であり、\(\text{(II)} \implies \text{(I)}\) と \(\text{(II)} \implies \text{(III)}\) は比較的容易に示せる。手間がかかるのは (II) を示すことで、藤﨑本では \(\text{(I)} \implies \text{(II)}\) も \(\text{(III)} \implies \text{(II)}\) も有限群論のやや高度な定理・補題を駆使して、ごく僅かな手がかりをかき集めて強い結論を引き出すという構成になっている。
そこで、以下では次のように証明の構成を変更してお届けする。
- 第4項
(IV) \(G\) は位数 \(p\) の正規部分群を持つ
を加え、(I)〜(IV) がすべて同値であることを証明することに目標を変更する。 - まず、「\(\text{(II)} \implies \text{(I)}\)」と「\(\text{(II)} \implies \text{(III)}\)」を証明する。
- 続いて、
- \(\text{(IV)} \implies \text{(II)}\)
- \(\text{(I)} \implies \text{(IV)}\)
- \(\text{(III)} \implies \text{(IV)}\)
の順に証明する。
では順に見て行こう。なお、「ガロア理論入門ノート」でカバーされていない予備知識をいくつか使うので、それは逐一挙げていくことにする。それらの証明は、ここでは触れない。
- \(\text{(II)} \implies \text{(I)}\) ここでは、予備知識として次のことを使う。
\(p\) が素数のとき、\(a \not\equiv 0 \pmod{p}\) である \(a\) は \(\tmod{p}\) での「逆数」を持つ。つまり \(ab \equiv 1 \pmod{p}\) となる \(b\) が存在する。
証明はここでは省略。興味のある方は素数を法とする合同式の性質に当たって欲しい。フェルマーの小定理を使ってよければ、逆数を \(a^{p-2}\) という具体的な形で書くこともできる。
\(\tmod{p}\) での、\(1\) 次の係数 \(\not\equiv 0\) の \(1\) 次式の全体が、合成に関してなす群を \(A\) とする(上に引用した性質から、このような \(1\) 次式の逆変換も同じ形の \(1\) 次式で表せることがわかり、群をなすことが言える。また、\(\tmod{p}\) で考えているので、\(1\) 次式の係数(定数項含む)は実質的に有限通りの違いしかないので、\(A\) は有限群となる)。
仮定 (II) より、\(G\) は \(A\) の部分群と同型なので、\(A\) が可解群であることを示せば (I) が言える。
まず、\(A\) の \(1\) 次式のうち、定数ずらしの \(x+b\) の形をしたものの全体を \(B\) とすると、\(B\) は \(A\) の部分群である。また、\(A\) の \(1\) 次式のうち、定数項 \(\equiv 0\) の \(ax\) の正比例の形のもの全体を \(C\) とすると、\(C\) も \(A\) の部分群である。\(B\), \(C\) はともに可換群である(ここでは使わないが、\(B\), \(C\) は巡回群にもなっている。\(B\) は、\(1\) ずらす \(1\) 次式 \(x+1\) を繰り返し合成すれば \(B\) のどの \(1\) 次式も作れるからただちに巡回群とわかる。一方、\(C\) が巡回群であることを示すには、素数を法とする合同式の更なる性質「\(p\) がどんな素数でも \(\tmod{p}\) での原始根が存在する」を要するが、その証明はここでは触れない)。
また、\(1\) 次式 \(ax+b\) は \(C\) の \(a\) 倍変換 \(ax\) と \(B\) の \(+b\) 変換 \(x+b\) の合成で作れるから、\(A = BC\) である。
\(B\) が \(A\) の正規部分群であることを示す。\(A\) の元は \(gh \quad (g \in B, h \in C)\) と書けるので示すべきことは \(ghB(gh)^{-1} = ghBh^{-1}g^{-1} \subset B\) だが、\(g \in B\) より \(hBh^{-1} \subset B\) を示せば十分。よって \(\sigma \in B\) に対し \(h\sigma h^{-1} \in B\) が言えればよい。
\(\sigma\), \(h\) を表す \(1\) 次式をそれぞれ \(x+b\), \(ax\) とおくと、\(h\sigma h^{-1}\) は \(a^{-1}x\), \(x+b\), \(ax\) の合成で表され、その \(1\) 次式は
\[ a(a^{-1}x+b) = x+ab \]
となって定数ずらし変換だから、\(B\) に属する。すなわち \(h\sigma h^{-1} \in B\) が言えた。すると、
\[ A/B = BC/B \cong C \quad (\because B \cap C = \{e\}) \]
で、\(B\), \(C\) ともに可換群なので \(A\) は可解群。\(\square\)※ 「\(A/B \cong C\)」というのは、「定数項の違いを無視すれば、\(1\) 次式の合成は \(1\) 次の係数の積のみで表される」ということで、実は当たり前の話。
※ 実は「\(A\) が可解」を示すだけなら、わざわざ \(B \cap C = \{e\}\) に言及して \(BC/B \cong C\) を確かめなくても、\(BC/B\) が \(C\) の部分群と同型、というだけで十分なのか…。まあそこまですると却って理解しづらくなる気もするし、これでいいか。
- \(\text{(II)} \implies \text{(III)}\) 根の番号を振り直すと \(G\) の変換は添字に関する \(1\) 次式で表されるので、異なる \(2\) 根 \(\alpha_{i}\), \(\alpha_{j}\) を固定するような \(G\) の変換は恒等変換に限られる。よって、\(K(\alpha_{i}, \alpha_{j})\) に対応するガロア群は単位群 \(\{e\}\) だから、ガロア理論の基本定理より \(L=K(\alpha_{i}, \alpha_{j})\) である。\(\square\)
- \(\text{(IV)} \implies \text{(II)}\) ここでは、予備知識として次のことを使う。
大きさ(位数)が素数の群は必ず巡回群になる
これは
\(G\) の部分群 \(H\) の大きさ(位数)\(\zettaiti{H}\) は \(G\) の大きさ(位数)\(\zettaiti{G}\) の約数になる
ことを利用して示せる。いずれもここでは証明は述べないが、有限群論の最も基本的な定理なので、類書を当たれば必ず載っているはず(なお、後者はガロア群とその部分群に限定すれば、\([L:L^{G}] = [L:L^{H}] [L^{H}:L^{G}]\) から従う \(\zettaiti{G} = \zettaiti{H} [L^{H}:L^{G}]\) によって言える)。
仮定 (IV) の正規部分群を \(N\) とする。\(p\) が素数なので、\(N\) は大きさ(位数)\(p\) の巡回群で、単一の元 \(\rho\) によって \(N=\langle \rho\rangle\) と生成される。
\(N\) を \(\{1, \dots, p\}\) に対する置換群として見たとき、あらかじめ根の番号を適当に振り直せば、\(\rho\) は巡回置換 \(\rho = (1 \; 2\; \dots \; p)\) だとしてよい。このとき \(\rho\) は \(\tmod p\) で \(+1\) する変換
\[ \rho(x) \equiv x+1 \pmod{p}\]
として表され、\(N\) の元は \(x+b \pmod{p}\) の形の \(1\) 次式で表される。\(N\) が \(G\) の正規部分群なので、\(g \in G\) に対して \(g\rho g^{-1} \in N\) だから、\(g\rho g^{-1} = \rho^{a}\) とおける。
すると \(g\rho = \rho^{a}g\) なので、
\begin{align}
g\rho (x) &= \rho^{a}g (x) & (x=1,\dots, p) \notag\\
\label{eq:32-1}
\therefore g(x+1) &\equiv g(x) + a \pmod{p} & (x=1,\dots, p)
\end{align}
\(a\) が \(x\) によらない定数なので、\eqref{eq:32-1}より \(g(1), g(2), \dots, g(p)\)は \(\tmod{p}\) で公差 \(a\) の等差数列になる。よって
\[ g(x) \equiv ax+b \pmod{p} \quad (x=1,\dots, p) \]
と表せる。\(\square\)※ 藤﨑本では \(N\) とは別に「\(p\) を固定する \(G\) の部分群」を \(H\) と置き、要素数を数えるとか「原始置換群」というものの性質を利用するなど高度な議論を行って \(G=NH\) を導く…という流れになっているが、目的が (II) を示すことだけならその辺りの議論はほぼスキップできる、という次第。
- \(\text{(I)} \implies \text{(IV)}\) 「可換な正規部分群がある」「その位数は \(p\)」という流れで示す。
ここでは、以下の予備知識を使う。一般に、群 \(G\) に対して交換子群を \(\mathcal{D}(G) = [G, G]\) とおき、\(\mathcal{D}\) の作用の繰り返しを
\[ \mathcal{D}^{k}(G) = \mathcal{D}(\mathcal{D}^{k-1}(G)), \mathcal{D}^{0}(G) = G \]
によって定める。このとき、列
\[ G = \mathcal{D}^{0}(G) \supset \mathcal{D}^{1}(G) \supset \mathcal{D}^{2}(G) \supset \mathcal{D}^{3}(G) \supset \dots \]
が有限回で単位群 \(\{e\}\) に達することと \(G\) が可解群であることは同値。一般に、\(N\) が群 \(G\) の正規部分群のとき、\(\mathcal{D}(N) = [N, N]\) も \(G\) の正規部分群。
実際にはこれらのうち一部分だけを組み合わせるだけで以下の議論には十分だが、それだとその発想がどういう背景から出てきたのかさっぱり見て取れない流れになってしまいそうなので、上のような形で触れておくことにする。
step.1 可換な正規部分群の存在
\(G\) の極小な正規部分群(単位群ではなく、それより真に小さな \(G\) の正規部分群は単位群しかないような正規部分群)の \(1\) つを \(N\) とする(\(1 < \zettaiti{G} < \infty\) よりそのような \(N\) は必ず存在する)。\(G\) が可解だから部分群 \(N\) も可解で、よって交換子群 \(\mathcal{D}(N)\) は \(N\) の真部分群。また \(N \lnsg G\) より \(\mathcal{D}(N) \lnsg G\)。すると \(N\) の極小性から \(\mathcal{D}(N) = [N, N] = \{e\}\) でなければならない。よって \(N\) は可換群(次のようにしてもいい。\(G\) の可解性から従う有限列
\[ G = \mathcal{D}^{0}(G) \supset \mathcal{D}^{1}(G) \supset \dots \supset
\mathcal{D}^{r}(G) \supset \mathcal{D}^{r+1}(G) = \{e\} \]
は、帰納的にすべて \(G\) の正規部分群であり、単位群になる直前の \(\mathcal{D}^{r}(G)\) を \(N\) とおけば、これは可換でもある)。step.2 \(N\) は根の集合 \(\{\alpha_{1}, \dots, \alpha_{p}\}\) に対して推移的に作用する
\(f(X)\) の任意の \(2\) 根 \(\alpha\), \(\beta\) に対し、\(\alpha\) を \(\beta\) に移すような \(N\) の元があることを示す。それは、\(N\) に対応する中間体 \(M\) 上で \(f(X)\) が既約であることと同値(なぜならば、\(\Gal(L/M)=N\) によって
\[ \text{$\alpha$ を $\beta$ に移すような $N$ の元がある} \iff
\text{$\alpha$, $\beta$ は $M$ 上で共役} \]
であり、\(f(X)\) の任意の \(2\) 根が \(M\) 上で共役ということは \(f(X)\) が \(M\) 上で既約ということだから)。\(N\) が \(G\) の正規部分群だったから、\(M\) は \(K\) の(有限次)正規拡大。すると、次の補題から、\(f(X)\) は \(M\) 上既約(後述)。
【補題】
\(f(X)\) は \(K\) 上既約な多項式(素数次とは限定しない)、\(L\) は \(f(X)\) の \(K\) 上の最小分解体、\(M\) は \(K\) と \(L\) の中間体で、\(K\) の正規拡大とする。このとき、\(f(X)\) の \(M\) 上での既約因子はすべて同じ次数。【証明】\(f(X)\) の根 \(\alpha\), \(\beta\) の \(M\) 上の最小多項式をそれぞれ \(d_{1}(X)\), \(d_{2}(X)\) とする。\(\Gal(L/K)\) の元で \(\alpha\) を \(\beta\) に移すものを \(\sigma\) とする(\(f(X)\) が \(K\) 上既約なのでそのような \(\sigma\) は存在する)。
\(d_{1}(\alpha)=0\) に \(\sigma\) を作用させると \({d_{1}}^{\sigma}(\sigma(\alpha)) = {d_{1}}^{\sigma}(\beta) = 0\) となる。ここで、\({d_{1}}^{\sigma}(X)\)は \(d_{1}(X)\) の各係数を \(\sigma\) で移したものである。
中間体 \(M\) が \(K\) の正規拡大であることから \(\sigma(M)=M\) なので、\({d_{1}}^{\sigma}(X)\) は \(M\) 係数である。よって \({d_{1}}^{\sigma}(X)\) は \(d_{2}(X)\) で割り切れる。従って次数について \(d_{2} \leqq d_{1}\) がなりたつが、\(\alpha\), \(\beta\) を入れ替えて同様の議論を行えば逆向きの不等号も言えるので、結局 \(d_{1}\), \(d_{2}\) の次数は等しい。(補題の証明終わり)
補題によって、\(M\) 上では素数 \(p\) 次の \(f(X)\) が同じ次数の既約因子の積に分解するので、\(f(X)\) は既約なままか、\(1\) 次式の積に分解し尽くすかのどちらかしかない。後者の場合 \(M=L\), \(N=\{e\}\) となってしまって矛盾。よって \(f(X)\) は \(M\) 上既約。\(\square\)
step 3. \(N\) の単位元以外の元はすべての根を動かす
\(N\) の元のうち、\(f(X)\) のいずれかの根を固定するものは単位元 \(e\) しかないことを示す。\(\sigma \in N\) が根 \(\alpha\) を固定するとする。\(\beta\) を他の任意の根として、\(\alpha\) を \(\beta\) に移す \(N\) の元を \(\tau\) とすると(step 2. によってそのような \(\tau\) の存在が保証される)、\(\tau\sigma\tau^{-1}\) は \(\beta\) を固定する。ところが \(N\) は可換だったので \(\tau\sigma\tau^{-1}=\sigma\)。つまり \(\sigma(\beta)=\beta\) である。よって \(\sigma\) は任意の根を固定するので、\(\sigma = e\)\(\square\)
step 4. \(\zettaiti{N}=p\)
\(N\) に対応する中間体を \(M\) とする。\(f(X)\) の根 \(\alpha\) に対し、\(\Gal(L/M(\alpha))\) は \(N\) の部分群で \(\alpha\) を固定するが、step 3. よりそれは単位群 \(\{e\}\) である。よって \(M(\alpha)=L\) であるから、
\[ \zettaiti{N} = [L:M] = [M(\alpha):M] = p \]
である。\(\square\)この step 1.〜4. は藤﨑本に沿って進めたもので、有限群論の枠内で書かれた議論を一部代数方程式のガロア理論の話に焼き直したものだが、ガロア理論の成果をうまく利用すればもう少し簡素化できそうな気がするものの、非才の私にはそれは無理だった。
この \(\text{(I)} \implies \text{(IV)}\) の話はおそらく「素数 \(p\) 次の既約な方程式がべき根で解ける場合は、最後のべき根は必ず \(p\) 乗根になる」ということが言えて、それに対応するのだろうが、その線で step 1.〜4. を圧縮・簡素化するのはどうもうまく行かなかった。ガロア自身が示していたからにはおそらくそこまで高度な知識は必要としないのだろうが、一体どうすればいいのやら。
【2014, 11/8】 step.1 については一応群論の知識を使わずに解決できた。
- \(\text{(III)} \implies \text{(IV)}\)「位数 \(p\) の部分群がある」「それは正規部分群」という順に証明する。step 1. \(G\) の構造分析
\(G\) の中で、「固定される根を持つ元」と「すべての根を動かす元」がどのように分布しているのか調べる。\(G\) の元のうち、\(f(X)\) の根 \(\alpha_{i}\) を固定するもの全体の部分群 \(\Gal(L/K(\alpha_{i}))\) を \(G_{i}\) とする(\(i=1,\dots,p\))。
\begin{align*}
[L:K] &= [L:K(\alpha_{i})][K(\alpha_{i}):K] \\
\therefore \zettaiti{G} &= \zettaiti{G_{i}} \times p
\end{align*}
より
\begin{equation}
\label{eq:32-4}
\zettaiti{G_{i}} = \dfrac{\zettaiti{G}}{p}
\end{equation}
である。さらに、仮定 (III) から、異なる \(2\) 根 \(\alpha_{i}\), \(\alpha_{j}\) を共に固定する \(G\) の元は \(e\) のみだから、
\begin{equation}
\label{eq:32-5}
G_{i} \cap G_{j} = \{e\} \quad (i \ne j)
\end{equation}
である。よって、\(S=G_{1} \cup \dots \cup G_{p}\) と置いて「固定される根を持つ \(G\) の元の個数」を数えると
\begin{align*}
\zettaiti{S} &= 1 + \sum_{i=1}^{p} (\zettaiti{G_{i}} – 1) \quad (\because
\eqref{eq:32-5}) \\
&= 1 + \Bigl( \dfrac{\zettaiti{G}}{p} – 1 \Bigr) \times p
\quad (\because \eqref{eq:32-4})\\
&= \zettaiti{G} + 1 – p \\
\therefore \zettaiti{G} &= \zettaiti{S} + (p-1)
\end{align*}よって、\(G\) は「すべての根を動かす元」をちょうど \(p-1\:(>0)\) 個持っている。step 2. \(G\) は位数 \(p\) の部分群を持つ
step 1. の、すべての根を動かす元の1つを \(\rho\) とする。\(\rho\) を根の添字に対する置換と見て、共通要素を持たない巡回置換の積の形に表しておく。
\[ \rho = (a \dots b) (c \dots d) \dotsm (g \dots h) \]
仮定より、この右辺には \(1\) から \(p\) までのすべての数が現れる。また、長さが \(1\) の巡回置換は現れない。右辺の巡回置換の任意の1つ、例えば \((a \dots b)\) を選び、その長さを \(l\) とする。すると、\(\rho\) を \(l\) 乗すると \({\underbrace{(a \dots b)}_{\text{長さ $l$}}}^{l}\) は単位元になって消えてしまうから
\[ \rho^{l} = (c \dots d)^{l} \dotsm (g \dots h)^{l} \]
である。すると \(\rho^{l}\) は \(l \geqq 2\) 個の根を固定する \(G\) の元だから、単位元 \(e\) である。これより、残りの要素 \((c \dots d)^{l}, \dots, (g \dots h)^{l}\) もすべて単位元になる。よって巡回置換 \((c \dots d), \dots, (g \dots h)\) の長さはすべて \(l\) の約数にならなければいけない。始めに \((a \dots b)\) を選ぶとき、\(\rho\) の巡回置換の中で最短のものを選ぶことができるから、今の議論からすべての巡回置換の長さは \(l\) に等しくなければならない。すると
\[ \rho = \overbrace{\underbrace{(a \dots b)}_{\text{長さ $l$}}
\underbrace{(c \dots d)}_{\text{長さ $l$}} \dotsm \underbrace{(g
\dots h)}_{\text{長さ $l$}}}^{\text{長さの和は $p$}} \]
となって、\(l\) は素数 \(p\) の約数である。これと \(l>1\) より \(l=p\)、すなわち \(\rho\) は長さ \(p\) の単一の巡回置換である。これより、\(G\) は位数 \(p\) の巡回群 \(N= \langle \rho \rangle\) を部分群に持つ。\(\square\)step 3. \(N\) は \(G\) の正規部分群
\(N\) の元のうち、\(e\) 以外の \(\rho, \rho^{2}, \dots, \rho^{p-1}\) の \(p-1\) 個はいずれも「すべての根を動かす」ような \(G\) の元だから、step 1. の \(p-1\) 個の「空席」は丁度これらで埋まっている。
\(\forall g \in G\) に対し、\(g\rho g^{-1}\) はすべての根を動かすから、前段落で示したことから、これは \(\rho^{1}, \dots, \rho^{p-1}\) のどれか。つまり \(g \rho g^{-1} \in N\) よって \(N=\langle\rho\rangle\) は \(gNg^{-1} \subset N\) をみたすから、\(N\) は \(G\) の正規部分群。\(\square\)
※ この step 2. は有限群の Cauchy の定理を使えば直ちに得られる(\(G\) は素数 \(p\) 次の既約な \(f(X)\) のガロア群なので \(\zettaiti{G}\) は \(p\) の倍数だから)。ただ、ガロアは Cauchy の定理は使っていなかったはずで、その上 Cauchy の定理はわりと大掛かりな証明か、さもなければ技巧的な証明を要するので、ここでは使用を避けて、代わりに仮定 (III) を活用することで無理なく位数 \(p\) の部分群の存在を導いてみた(これがガロアの行った議論と同じかどうかはわからないけれど)。
コメントを残す