\(\newcommand{\kumiawase}[2]{{}_{#1}\text{C}_{#2}}\)
今年も Mathpower の数学の決闘の問題を1問思いついて、提出してみたのですが、今年は選題する側に回ってしまったので、私の問題は没ということになってしまいました(笑)。無念を晴らすために、ここで公開することにします。
問題
 多項式 \(f(p)\) を
多項式 \(f(p)\) を
\begin{equation}
\label{eq:mathpower2018-1}
f(p) = \sum_{k=0}^{2018} \kumiawase{2018+k}{k} p^{2019}(1-p)^{k}
\end{equation}
によって定めます。ただし、\(\kumiawase{n}{r}\) は二項係数です。
\(\dfrac{f'(2)}{2^{2018}\kumiawase{4037}{2018}}\) を求めてください。
この図は何のためについているのか…ということがヒントです。
解答
まず、\(0<p<1\) の場合を考える。\(f(p)\) は
\(1\) 回の対戦では確率 \(p\) で勝つ相手と繰り返し対戦したときに、自分が先に \(2019\) 勝を挙げる確率
である(\(2019\) 勝目を挙げる直前の負け数 \(k\) を、\(k=0\) から \(k=2018\) まで排反な場合分けをして足し合わせると\eqref{eq:mathpower2018-1}になる)。
この確率は、次のように言い換えることもできる。
\(1\) 回の対戦では確率 \(p\) で勝つ相手に、\(4037\) 番勝負で勝ち越す確率
したがって \(f(p)\) は次のようにも表せる。
\begin{equation}
\label{eq:mathpower2018-2}
f(p) = \sum_{k=2019}^{4037} \kumiawase{4037}{k} p^{k} (1-p)^{4037-k}
\end{equation}
これは、\(4037\) 回の対戦で勝ち数 \(k\) が \(2019\) 以上になる確率を、排反な場合分けで足し合わせたものである。
\(\eqref{eq:mathpower2018-1}=\eqref{eq:mathpower2018-2}\) となる理由の補足
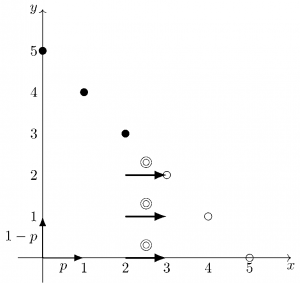
\(5\) 番勝負に縮小して考える。\(1\) 回の対戦での勝ち・負けにそれぞれ→・ ↑を対応させて、対戦結果に応じて原点から移動させると、\(5\) 回対戦した結果は図の○か●のいずれかになる(○が勝ち越し、●が負け越し)。
原点から○か●に到達する経路のすべてを全体集合としよう。すべての経路は排反である。\eqref{eq:mathpower2018-2}は○に達する経路の確率の和に相当し、一方\eqref{eq:mathpower2018-1}は◎印のいずれかの矢印を通る経路の確率の和に相当する。
○に達する経路はすべて◎の矢印のどれかを通る。逆に、◎を通る経路はどれも○に達する。したがって、○に達する経路の全体と◎を通る経路の全体は一致するので、それらの確率の和である\eqref{eq:mathpower2018-1}と\eqref{eq:mathpower2018-2}は等しい。
\eqref{eq:mathpower2018-1}と\eqref{eq:mathpower2018-2}のそれぞれの右辺は、\(0<p<1\) の任意の \(p\) に対して等しいので、多項式として一致する。
したがって、任意の \(p\) に対して\eqref{eq:mathpower2018-2}を使ってよく、
\begin{align*}
f'(p) &= \sum_{k=2019}^{4037} \kumiawase{4037}{k} \bigl\{ k p^{k-1}(1-p)^{4037-k} – (4037-k) p^{k}(1-p)^{4036-k} \bigr\} \\
&= \sum_{k=2019}^{4037} \bigl\{ k \kumiawase{4037}{k} p^{k-1}(1-p)^{4037-k} – (4037-k) \kumiawase{4037}{4037-k} p^{k} (1-p)^{4036-k} \bigr\}
\end{align*}
ここで、\(r>n\) や \(r<0\) のときに \(\kumiawase{n}{r}=0\) と定めれば \(n \geqq 0\) の任意の \(n\), \(r\) に対して
\[ r \kumiawase{n}{r} = n \kumiawase{n-1}{r-1} \]
がなりたつことに注意すると
\begin{align}
f'(p) &= \sum_{k=2019}^{4037} \bigl\{ 4037 \kumiawase{4036}{k-1} p^{k-1}(1-p)^{4037-k} – 4037 \kumiawase{4036}{4036-k} p^{k} (1-p)^{4036-k} \bigr\} \notag\\
\label{eq:mathpower2018-3}
&= 4037 \sum_{k=2019}^{4037} \bigl\{ \kumiawase{4036}{k-1} p^{k-1}(1-p)^{4037-k} – \kumiawase{4036}{k} p^{k} (1-p)^{4036-k} \bigr\}
\end{align}
である。\eqref{eq:mathpower2018-3}の中括弧内が \(k\) に関する階差型になっていることから和が計算できて、
\begin{equation}
\label{eq:mathpower2018-4}
f'(p) = 4037 \kumiawase{4036}{2018} p^{2018}(1-p)^{2018}
\end{equation}
である。
よって
\begin{align*}
f'(2) &= 4037 \kumiawase{4036}{2018} 2^{2018} \\
\therefore \frac{f'(2)}{2^{2018}\kumiawase{4037}{2018}} &= \frac{4037 \kumiawase{4036}{2018}}{\kumiawase{4037}{2018}}
= \boxed{2019}
\end{align*}
考察など
元ネタは、またしても東京出版「大学への数学 解法の探求・確率」です。発展編「破産の確率」の最後の所で
\[ f(p) = p^{4} + \kumiawase{4}{1}p^{4}(1-p) + \kumiawase{5}{2}p^{4}(1-p)^{2} + \kumiawase{6}{3}p^{4}(1-p)^{3} \]
を \(p=0.5\) の近くで \(1\) 次近似した結果が出ていますが、自分で微分してみると
\[ f'(p) = 140p^{3}(1-p)^{3} \]
とやけにきれいな形の式になったので、「これは偶然ではなく何か背景があるのではないか?」と調べているうちに気づいたことを問題にしました。
上で、\eqref{eq:mathpower2018-1}と\eqref{eq:mathpower2018-2}が一致することを意味づけで示しました。ここで使った「○敗する前に○勝する」と「○回対戦して、○勝以上挙げる」の間の言い換えは、受験数学的にはそこそこ重要な立式テクニックではあって、実際「解法の探求・確率」中の別のページでもしばしば顔を出しています。ただ、「\(\eqref{eq:mathpower2018-1}=\eqref{eq:mathpower2018-2}\)」という形ではあんまり有名ではないのではないでしょうか?要するに、負の二項分布 \(\text{NB}(2019,p)\) の累積分布関数と、普通の二項分布 \(\text{Bi}(4037,p)\) の累積分布関数を \(1\) から引いたものが(細かい違いを除けば、本質的には)一致するということですが、こういう一般的な形で系統的に成立するということは、私はつい先日気づいたばかりです。
なお、図を参考にすると、確率の意味づけによらない式変形だけで\eqref{eq:mathpower2018-1}を \eqref{eq:mathpower2018-2}に変形することもでき、その方針なら \(p\) の範囲を一旦 \(0<p<1\) に制限する、ということをしなくても答が出せます。興味のある方は考えてみてください。
また、二項分布の確率分布関数を \(p\) で微分すると\eqref{eq:mathpower2018-3}のように階差型になる、というのもその時初めて気づいたのですが、ひょっとするとこれも私が知らなかっただけの有名事実なのでしょうか?
あと、\eqref{eq:mathpower2018-4}は \(4037\) の因子を除くと \(\kumiawase{4036}{2018} p^{2018}(1-p)^{2018}\) で、これは「\(4036\) 回対戦して \(2018\) 勝 \(2018\) 敗の確率」つまり「\(4037\) 番勝負が最終戦までもつれる確率」です。そのちょうど \(4037\) 倍になる、ということに何か意味がありそうな気もしますが、今の所うまい意味づけで直接\eqref{eq:mathpower2018-4}を導く道は見つけられていません。「こうすればできるよ!」といううまい手がありましたら、コメント欄を通じて教えて頂ければと思います。
\begin{equation}
\label{eq:mathpower2018-toi-1}
\int_{p}^{1} \frac{z^{k-1}(1-z)^{n-k}}{B(k,n-k+1)}dz = \sum_{x=0}^{k-1} \kumiawase{n}{x} p^{x}(1-p)^{n-x}
\end{equation}
(\(n\) は自然数、\(k\) は \(1\) から \(n\) までの自然数)
当該箇所では、\eqref{eq:mathpower2018-toi-1}を示す道筋は、左辺を \(k\) の関数 \(I(k)\) とおき部分積分によって \(\{I(k)\}\) の階差型漸化式を導く…という流れによっています。途中で、\((n-k+1)B(k,n-k+1) = \frac{1}{\kumiawase{n}{k-1}}\) となることも使っています。
\eqref{eq:mathpower2018-toi-1}の両辺を \(1\) から引くと
\begin{equation}
\label{eq:mathpower2018-toi-2}
\int_{0}^{p} \frac{z^{k-1}(1-z)^{n-k}}{B(k,n-k+1)}dz = \sum_{x=k}^{n} \kumiawase{n}{x} p^{x}(1-p)^{n-x}
\end{equation}
で、\eqref{eq:mathpower2018-toi-2}の右辺は\eqref{eq:mathpower2018-2}右辺の一般化、\eqref{eq:mathpower2018-toi-2}の左辺を \(p\) で微分したものが\eqref{eq:mathpower2018-4}右辺の一般化です。したがって、\eqref{eq:mathpower2018-toi-2}(あるいは\eqref{eq:mathpower2018-toi-1})は本記事で導いた関係と本質的には同じもので、それは「ベータ分布と二項分布の関係」だ、という背景をこの本が明らかにしている、と見られますね。
別解
\eqref{eq:mathpower2018-2}に変換せず、\eqref{eq:mathpower2018-1}のまま計算することも不可能ではありません。
\begin{align}
f'(p) &= \sum_{k=0}^{2018} \kumiawase{2018+k}{k} \bigl\{ 2019 p^{2018} (1-p)^{k} – k p^{2019} (1-p)^{k-1} \bigr\} \notag\\
\therefore f'(2) &= \sum_{k=0}^{2018} \kumiawase{2018+k}{k} \bigl\{ 2019 \cdot 2^{2018} (-1)^{k} – k\cdot 2^{2019}(-1)^{k-1} \bigr\} \notag\\
\label{eq:mathpower2018-5}
\therefore \frac{f'(2)}{2^{2018}} &= \sum_{k=0}^{2018} \kumiawase{2018+k}{k} (-1)^{k} (2019 + 2k)
\end{align}
ここで、\(g(k) = \kumiawase{2018+k}{2019} (-1)^{k}\) とおいてみると
\begin{align*}
g(k+1) – g(k) &= \kumiawase{2019+k}{2019} (-1)^{k+1} – \kumiawase{2018+k}{2019} (-1)^{k} \\
&= \frac{(-1)^{k+1}}{2019!} \bigl\{ \underbrace{(2019+k)(2018+k) \dots (1+k)}_{2019\text{個}} + \underbrace{(2018+k)(2017+k) \dots (1+k)k}_{2019\text{個}} \bigr\} \\
&= \frac{(-1)^{k+1}}{2019!} \underbrace{(2018+k) \dots (1+k)}_{2018\text{個}} (2019+k + k) \\
&= \frac{(-1)^{k+1}}{2019} \kumiawase{2018+k}{2018} (2019+2k)
\end{align*}
である。\(\kumiawase{2018+k}{k} = \kumiawase{2018+k}{2018}\) に注意すると\eqref{eq:mathpower2018-5}が階差の和に書けて、
\begin{align*}
\frac{f'(2)}{2^{2018}} &= -2019 \sum_{k=0}^{2018} \bigl\{ g(k+1) – g(k) \bigr\} \\
&= -2019 \bigl\{ g(2019) – g(0) \bigr\} \\
&= -2019 (\kumiawase{4037}{2019}(-1)^{2019} – \kumiawase{2018}{2019}(-1)^{0}) \\
&= 2019 \kumiawase{4037}{2018} \\
\therefore \frac{f'(2)}{2^{2018}\kumiawase{4037}{2018}} &= \boxed{2019}
\end{align*}
コメントを残す