\(\newcommand{\kumiawase}[2]{{}_{#1}\text{C}_{#2}}\require{color}\newcommand{\tintred}{red!40}\newcommand{\tintblue}{blue!40}\newcommand{\tintgreen}{green!40}\)
http://6504.teacup.com/aozoram/bbs/4127 で、面白い問題が紹介されていたので取り組んでみた。
http://6504.teacup.com/aozoram/bbs/4127 (3)の一般化
横軸を歩数、縦軸を座標(\(Z\) の値)とする座標平面上の経路で表すと、「\(\nearrow\)」と「\(\searrow\)」を \(n\) 個つなげた経路となる。確率は \(\dfrac{\text{経路数}}{2^{n}}\) なので経路数の問題に帰着できる。
経路の1対1対応
\(M_{n}=k\) の経路と \(T_{n}=k\) の経路の間に1対1対応が作れる。
\(T_{n}=2\) の経路→ \(M_{n}=2\) の経路
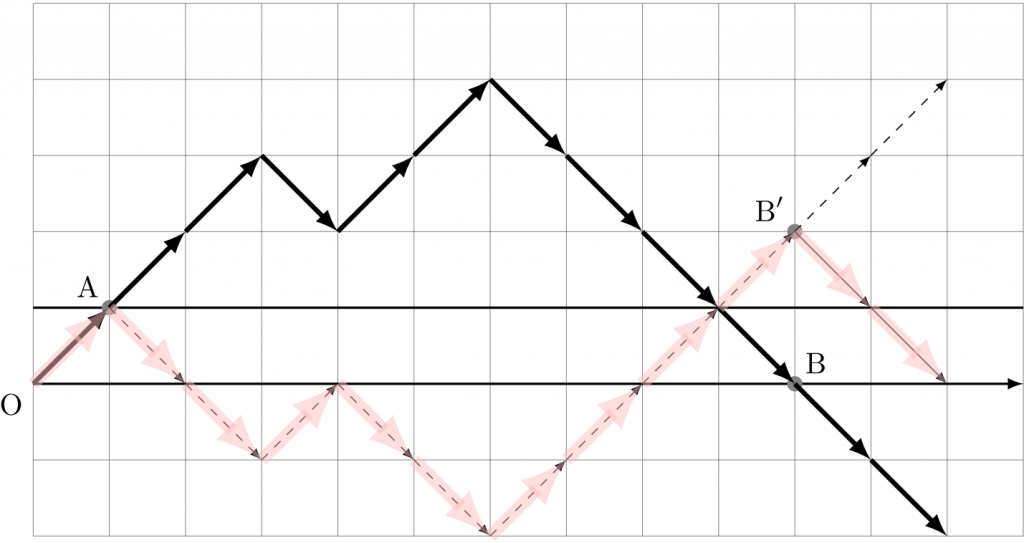
\(T_{n}=2\) の経路(図の黒の太線の矢印による折線)では \(0 \leqq Z \leqq 1\) の「帯」を \(2\) 回横切るわけだが、「横切った直後の点」に着目。図では A, B がそれらの点。
まず、最初の点 A から後の経路を上下反転(「\(\nearrow\)」と「\(\searrow\)」を入れ替え)した経路を作る。これで破線の矢印による経路ができる。このとき B は \(\text{B}’\) にうつっているが、\(\text{B}’\) から後の経路を再度上下反転する。すると細線の矢印による経路ができる。
こうやって作ってきた経路を繋いだ経路(図のピンク)は \(M_{n}=2\) の経路になっている。
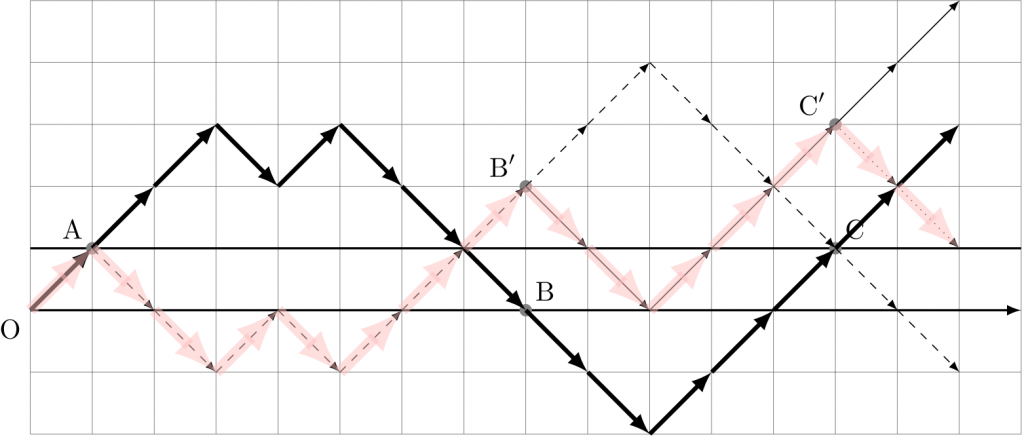
\(T_{n}=3\) の経路→ \(M_{n}=3\) の経路
\(T_{n}=3\) の経路についても同様に「横切った直後」の点 A, B, C を定め、それぞれの点(のうつり先)から後の経路を次々上下反転していくことで、\(M_{n}=3\) の経路が作れる。反転後にうつった点 \(\text{A}, \text{B}’, \text{C}’\) は、できあがった \(M_{n}=3\) の経路でそれぞれ「初めて高さ \(1\) に達した点」「初めて高さ \(2\) に達した点」「初めて高さ \(3\) に達した点」になっている(この関係は先ほどの \(T_{n}=2\) の経路と \(M_{n}=2\) の経路でも同じ)。
このようにして、\(T_{n}=k\) の経路から \(M_{n}=k\) の経路が作れる。これは、http://6504.teacup.com/aozoram/bbs/4130 の \(\omega \mapsto \omega’\) の写像とまったく同じ対応になっている。
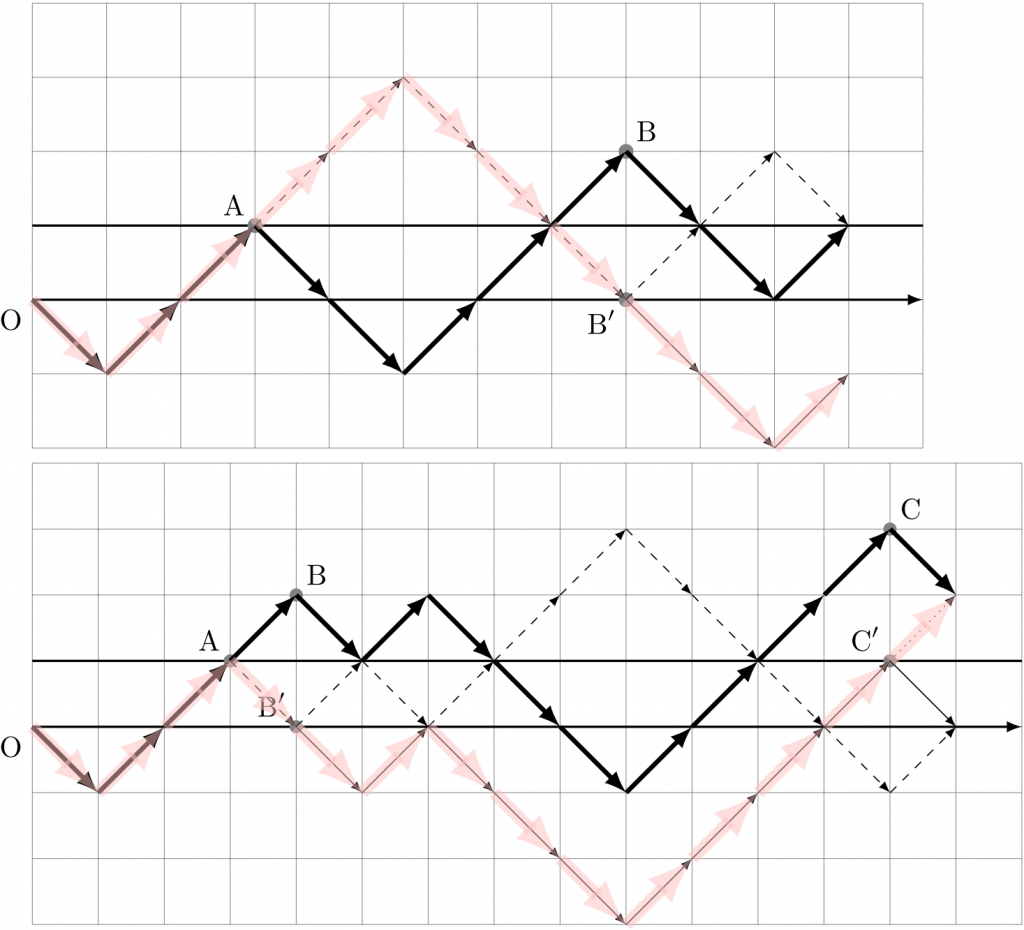
\(M_{n}=k\) の経路→\(T_{n}=k\) の経路
\(M_{n}=k\) の経路で、「初めて高さ \(1\) に達する点」「初めて高さ \(2\) に達する点」…を A, B, C,… とし、「A から後の経路を上下反転」「B(がうつった先)から後の経路を上下反転」「C(がうつった先)から後の経路を上下反転」…としていくと、\(T_{n}=k\) の経路ができる。
こうなる理由は次の通り。\(M_{n}=k\) の経路で、「A から B まで」や「B から C まで」などのそれぞれの部分は、次の特徴を持っている:「それぞれの出発点以下の高さをずっと進み続け、最後の 1 歩でのみ出発点より \(1\) だけ高い点に到達する」よって、上下を折り返すことによって、「A から \(\text{B}’\) まで」は「ずっと A 以上の高さを進み続け、最後の 1 歩でのみ A より \(1\) だけ低い点に到達する」という経路にうつるし、「\(\text{B}’\) から」の経路は「ずっと \(\text{B}’\) 以下の高さを進み続け、最後の 1 歩でのみ \(\text{B}’\) より \(1\) だけ高い点に到達する」ような経路にうつる。
その繰り返しなので、A, \(\text{B}’\), \(\text{C}’, \dotsc\) は \(Z=0\) と \(Z=1\) の上に交互に並んでいき、\(M_{n}=k\) の経路は \(T_{n}=k\) の経路にうつることになる。
\(T_{n}=k\) の経路が \(M_{n}=k\) の経路にうつる理由も同様。
このようにして、\(M_{n}=k\) の経路と \(T_{n}=k\) の経路の1対1の対応がつくので、経路数が一致し、確率も等しくなる。
\(M_{n}=k\) の経路数
これは http://aozoragakuen.sakura.ne.jp/probability/suiho2/node1.html のようなうまいカウント法を見つけられなかったので、別のやり方で…。
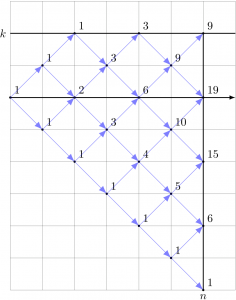
\(M_{n} \leqq k\) となる経路数を数えるには、図のように原点から出発し、高さが \(k+1\) に達しない経路数を書き入れ、横座標が \(n\) のライン上の経路数を加えればよい。この経路数は Pascal の三角形の法則(を横にしたもの)に従って足し合わされる。上の例の場合、
\[ \text{[$M_{n} \leqq k$ の経路数]} = \colorbox{\tintblue}{\(1+6+15+19+9\)} \]
である。
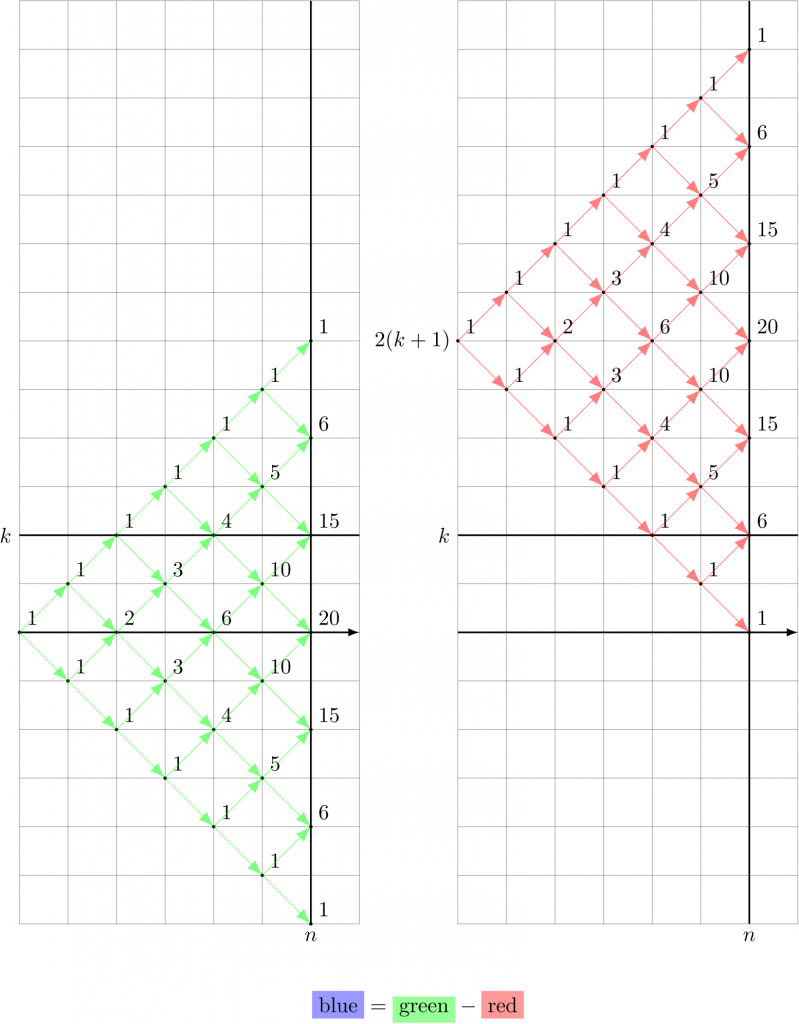
上の図の経路数は、下図左のように制限なしで普通に作った Pascal の三角形の経路数から、不適な経路数を引いても得られる。不適な経路は高さ \(k+1\) に達するものだから、初めて高さ \(k+1\) に達した点より前を上下反転して折り返すと、下図右のように点 \((0,2(k+1))\) から出発する経路数として表せる。
【2017, 11/22 追記】そうか、ここ、\(k+1\) に達した点の「前」を折り返すより、「後」を折り返した方がすっきり行きますね。そうすれば、わざわざ Pascal の三角形を 2 つ用意する必要はなくて、1 つの Pascal の三角形でかたがつく話になります。どうせ横座標 \(n\) で高さが \(k\) 以下になる経路数しか見る必要がないので、そういう経路を折り返せば横座標 \(n\) での高さが \(k+2\) 以上になる…と考えれば以下の計算も容易です。結果として http://aozoragakuen.sakura.ne.jp/probability/suiho2/node1.html の解との差がどんどん縮まってきますが…。
したがって、\(M_{n} \leqq k\) の経路数は、横座標が \(n\) での緑と赤の経路数のうち、高さ \(k\) 以下の範囲で「緑の経路数の合計」と「赤の経路数の合計」の差をとったものでもある。すなわち
\[ \text{[$M_{n} \leqq k$ の経路数]} = \colorbox{\tintgreen}{\(1+6+15+20+15\)} – (\colorbox{\tintred}{\(1+6\)}) = 15 + 20 + 15 \]
となる。
上図の場合、
\[ \text{[$M_{n} \leqq k$ の経路数]} = \colorbox{\tintgreen}{\(1+6+15+20\)} – (\colorbox{\tintred}{\(1+6\)}) = 15 + 20 \]
となっている。
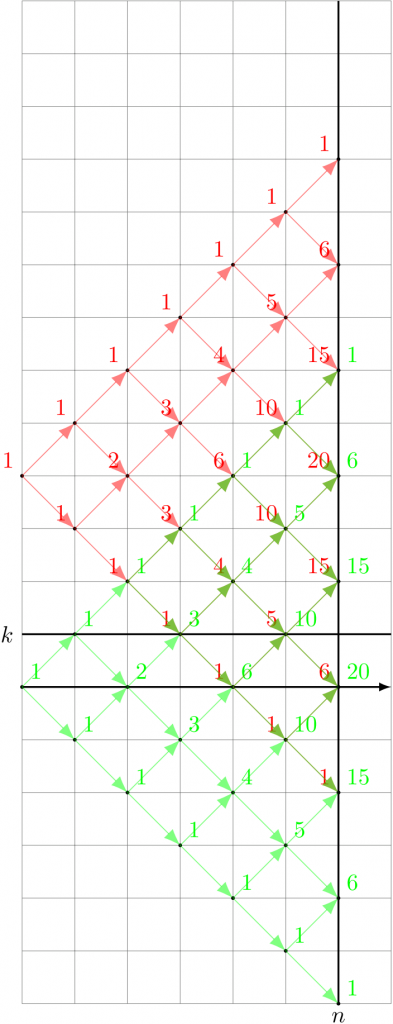
赤の Pascal 三角形を下に \(2(k+1)\) だけ平行移動すると緑の Pascal 三角形と同じになるので、次のようになる(ここで「経路数」というのはすべて「横座標が \(n\) の点」での値について言っている)。
\begin{gather*}
\colorbox{\tintred}{[赤の高さ $k$ 以下の経路数]} = \colorbox{\tintgreen}{[緑の高さ $-k-2$ 以下の経路数]} \\
\begin{split}
\therefore \text{[$M_{n} \leqq k$ の経路数]} &= \colorbox{\tintgreen}{[緑の高さ $k$ 以下の経路数]} – \colorbox{\tintred}{[赤の高さ $k$ 以下の経路数]} \\
&= \colorbox{\tintgreen}{[緑の高さ $k$ 以下の経路数]} – \colorbox{\tintgreen}{[緑の高さ $-k-2$ 以下の経路数]} \\
&= \colorbox{\tintgreen}{[緑の高さ $-k-1$ 以上 $k$ 以下の経路数]} \quad (k \geqq 0)
\end{split} \\
\begin{split}
\therefore \text{[$M_{n} = k$ の経路数]} &= \text{[$M_{n} \leqq k$ の経路数]} – \text{[$M_{n} \leqq k-1$ の経路数]} \quad (k \geqq 1) \\
&= \colorbox{\tintgreen}{[緑の高さ $-k-1$ の経路数]} + \colorbox{\tintgreen}{[緑の高さ $k$ の経路数]} \quad (k \geqq 1)
\end{split}
\end{gather*}
Pascal の三角形の対称性から、結局
\[ \text{[$M_{n} = k$ の経路数]} = \colorbox{\tintgreen}{[緑の高さ $k+1$ の経路数]} + \colorbox{\tintgreen}{[緑の高さ $k$ の経路数]} \]
で、この結果は \(k=0\) の場合も含めて正しい。
どの \(n\) に対しても、高さ \(k\), \(k+1\) にはどちらか一方にしか経路数は割り当てられないから、「割り当てられている方の経路数」が \(M_{n} = k\) の経路数であり、いずれにしろ \(1\) 個の \(\kumiawase{n}{\square}\) の形で表される。
\(\kumiawase{n}{r}\) の高さは \(n-2r\) だから、
\begin{align*}
n-2r = k &\iff r = \frac{n-k}{2} \\
n-2r = k+1 &\iff r= \frac{n-k-1}{2}
\end{align*}
で、\(n\), \(k\) の偶奇が一致するときは前者、一致しないときは後者になる。どちらの場合でも \(r= \Bigl\lfloor \dfrac{n-k}{2} \Bigr\rfloor\) と表せるので、
\[ \text{[$M_{n} = k$ の経路数]} = \kumiawase{n}{r} = \kumiawase{n}{\lfloor \frac{n-k}{2} \rfloor} \]
である。
この値を、\(n\) を固定して \(k=0,1,2,\dots\) に対する数列として見ると、
- \(n\) が偶数のとき
\[ a,b,b,c,c,d,d, \dotsc \]
という形の数列 - \(n\) が奇数のとき
\[ a,a,b,b,c,c, \dotsc \]
という形の数列
になっている。
※ なるほど、こうやって考えが整理されると、http://aozoragakuen.sakura.ne.jp/probability/suiho2/node1.html の数え方も理解が深まる。あっちは、\(M_{n} \geqq k\) となる経路数を、最終高さが \(k\) 以上か \(k\) 未満かで排反に分割して数えるとああなるんだ。\(k\) 以上のものはそのまま素直に緑の経路数で、一方 \(k\) 未満のものは最初に高さ \(k\) に達した点から先を上下折り返して、到達高さを \(k+1\) 以上の緑の経路数に翻訳して求めている。この考え方の場合、「\(k\) 以上か \(k\) 未満か」で場合分けする(とうまく行く)、というのが、言われないとなかなか気づきにくいかなあ。
コメントを残す