合同式で理解する正規部分群・その３

\(\DeclareMathOperator{\Ker}{Ker}
\DeclareMathOperator{\Img}{Im}
\)
前回、前々回の続きとして、今度はもう１つの同型定理を合同式と同値類で扱ってみる。

【定理】 \(G\) を群、\(M\), \(N\) を \(G\) の正規部分群とし、\(M \supset N\) とすると、\((G/N)/(M/N) \cong G/M\)

つまり、左辺を普通の分数であるかのように扱って「約分」してよい、というわけである。具体例を挙げよう。対称群 \(S_{4}\) は正規部分群として交代群 \(A_{4}\) とクラインの４元群 \(V_{4}\) を持ち、しかも \(V_{4}\) は \(A_{4}\) の部分群でもある。このとき、一番小さい群で残り２つを割った \(S_{4}/V_{4}\), \(A_{4}/V_{4}\) はそれぞれ \(S_{3}\), \(A_{3}\) と同型だったが、それらの「比」\(S_{3}/A_{3}\) が始めの２つの「比」\(S_{4}/A_{4}\) と同型になっている、というのが定理の言っていることになる。
\[ (S_{4}/V_{4}) / (A_{4}/V_{4}) \cong S_{3}/A_{3} \cong S_{4}/A_{4} \]
\(S_{3}/A_{3}\) と \(S_{4}/A_{4}\) はどちらも積を演算とする群 \(\{1,-1\}\) と同型なので、これは確かになりたっている。

普通、この同型定理を証明するときは、準同型定理
\[ G/\Ker f \cong \Img f \]
に帰着するために、上手く準同型写像を定めてやる、という流れをとる（ようだ）。もちろんそれは「簡潔」で「美しい」証明なのだが、しかしやはりその証明を「読む」立場の人からすれば、何が何やらさっぱりわからないままに終わってしまう話になっている。この定理はどんな意味があって、どういう描像で捉えることができて、その準同型写像の定義の仕方はどんな見通しの下に構想されたのか…といったことが皆目見当も付かないまま、無理矢理手を引かれて薮の中を最短コースで突っ切らされたも同然だからだ。

そこで、ここではもっとゆっくり、周りの景色を眺め、積極的に寄り道をしながら、この同型定理の意味や背景といったものに接していこう。

【第１段階】

まずは、結論の式 \((G/N)/(M/N) \cong G/M\) は一旦おいておいて、前回の１つ目の同型定理から得られる知見を確かめておこう。\(M\) が \(G\) の部分群なので、前回の１つ目の同型定理を \(H=M\) として適用できる。

今の場合 \(M \supset N\) なので、「\(M\) を同値類に分類する \(M\) の正規部分群」は \(M \cap N = N\)、つまり \(N\) そのものである。前回の同型定理では「\(N\) のうち、\(H\) の外にはみ出した部分」を削る必要があったが、今回は元々はみ出した部分がないので、最初から \(N\) 全体が \(M\) に対しても正規部分群になっているというわけだ。

このことの意義の１つは、\(N\) による同値類と \(M\) の関係が次の図のようになっている、ということである。これを確かめることが【第１段階】の目標になる。

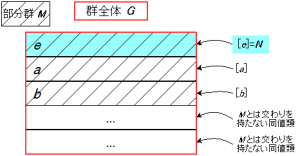
この図が言ってることはこうだ。

前回の同型定理のように、いちいち \(M\) からはみ出した部分を削って \([a]’\) という新しい集合を作ったりしなくても、\(M\)と交わりを持つ同値類 \([e], [a], [b], \dotsc\) が無加工で \(M\) を分類・分割する同値類としてそのまま使える。

この「はみ出さない」という性質、つまり
\begin{equation}
\label{eq:26-1}
a \in M \implies [a] \subset M
\end{equation}
は、我々の「群の合同式」を使って自然に示せる。\eqref{eq:26-1}を示すには、\(a \in M\) かつ \(a \equiv b\) なら \(b \in M\) となることを示せばよい。まず、\(a \equiv b\) より \(b = an \; (n \in N)\) とおける。すると、\(N \subset M\) より \(n \in M\) でもあるから、\(a \in M\) とあわせると
\[ b = \underbrace{a}_{\text{$M$の要素}} \underbrace{n}_{\text{$M$の要素}}
\]
となって \(b \in M\) が言えた。なぜならば、\(M\) は群をなすから、\(M\) の要素どうしの積はやはり \(M\) の要素になるからである。（なお、元々 \(M\) と交わりを持たない同値類が存在し得ることは前回の同型定理と同様。その様子は図からも明らかだろう）

【第２段階】

【第１段階】で着目した「\(N\) が \(M\) に対しても正規部分群になっている」という性質の意義を更に考えてみる。これは、\(M/N\) という商群が構成できるということを意味している。この商群は上の図だと \([e], [a], [b]\) という３つの同値類を要素とする集合で、
\[ M/N = \{[e], [a], [b]\} \]
が群になっているということである。一方商群 \(G/N\) は同値類 \([a]\) 全体の集合
\[ G/N = \{[e], [a], [b], \dotsc\} \]
がなす群だったから、\(M/N\) は \(G/N\) の部分集合だ。それが群にもなっているということは、\(M/N\) は \(G/N\) の部分群ということである。さて、この部分群は果たして正規部分群だろうか？【第２段階】ではこれを確かめてみよう。

正規部分群の定義として、ここまでの我々の流儀をここでも採用すると、確かめるべきことは「\(x \in G/N\), \(y \in M/N\) に対して、
\begin{equation}
\label{eq:26-2}
yx = xy’ \quad (y’ \in M/N)
\end{equation}
となる \(y’\) がとれるかどうか」である。

\(x\), \(y\) のとり方より \(x=[g], y=[m] \; (g \in G, m \in M)\) とおけるので、\eqref{eq:26-2}の左辺から式変形を始めると
\begin{equation}
\label{eq:26-3}
yx = [m][g] = [mg]
\end{equation}
である。ここで、\(M\) が \(G\) の正規部分群であることから \(mg = gm’ \; (m’ \in M)\) とおけるので、\eqref{eq:26-3}は以下のように変形を続行できる。
\begin{equation}
\label{eq:26-4}
[mg] = [gm’] = [g][m’]
\end{equation}
ここで、\(m’ \in M\) より \(y’=[m’]\) とおくと \(y’ \in M/N\) である。よって\eqref{eq:26-4}は更に
\[ [g][m’] = xy’ \quad (y’ \in M/N) \]
と「\eqref{eq:26-2}の右辺」に変形できる。これと\eqref{eq:26-3}\eqref{eq:26-4}から、\eqref{eq:26-2}の成立が示せた。よって、\(M/N\) は \(G/N\) の正規部分群である。

（ちょっと余談。他に前回の同型定理からわかることはあるだろうか。結論の式 \(H/(H \cap N) \cong (HN)/N\) は、今の場合は \(M/N \cong (MN)/N\) となるが、\(M \supset N\) より \(MN=M\) となるため結局 \(M/N \cong M/N\) となる。両辺が一致する自明な関係に帰着してしまったので、残念ながらこれと言った成果は得られない。つまり、前回の同型定理は、今の状況設定では、結論よりも途中の考察の方が実りある成果につながっているということになる）

【第３段階】

さて、そうすると、群 \(G/N\) にも、その正規部分群 \(M/N\) に基づく合同式や同値類を定めることができる。もちろん、\(M/N\) が生み出す合同式や同値類は \(N\) が生み出すそれらとは違うものだから、同じ記号を使って表すわけにはいかない。そこで、新しい合同式と同値類は、新しい記号を使って \(x \sim y\) や \(\langle x\rangle\) のように書くことにしよう。新旧の記号の違いを簡単に表でまとめてみる。
\[
\begin{array}{c|c|c}
\text{合同式} & a \equiv b & x \sim y \\
\text{両辺は何の要素？} & a,b \in G & x, y \in G/N \\
\text{正規部分群} & N & M/N \\
\text{同値類} & [a] & \langle x\rangle
\end{array}
\]
\(x,y \in G/N\) は \(x=[a], y=[b]\) のようにおけるので、「\(x \sim y\)」は「\([a] \sim [b]\)」と書け、「\(\langle x\rangle\)」は「\(\langle [a]\rangle\)」と書くことができる。

新しい同値類についての商群はどのように書けるだろうか。商群というのは「\(\text{親の群}/\text{正規部分群}\)」という書き方をするので、この場合は当然「\((G/N)/(M/N)\)」が商群である。つまり、新しい同値類 \(\langle x\rangle = \langle[a]\rangle\) は \((G/N)/(M/N)\) という集合の元ということになる。群 \(G/N\) とその商群 \((G/N)/(M/N)\) の関係を図示しておこう。

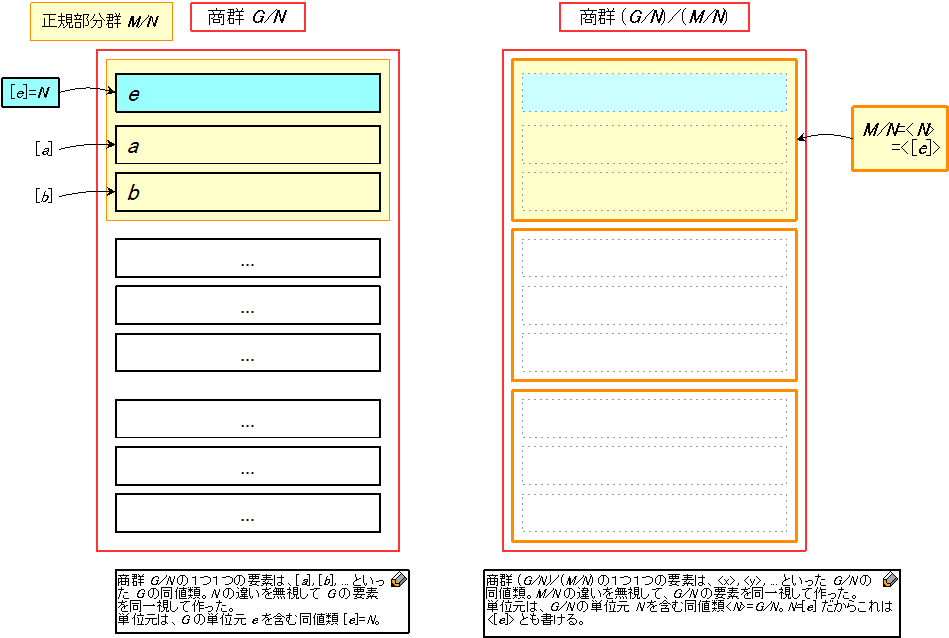
まだ色々と混乱している人も多いと思うので、図ではわかりにくい \(G/N\), \((G/N)/(M/N)\) の違いを式で書いておく。まず、繰り返しになるが \(G/N\) は
\[ G/N = \{[e], [a], [b], \dotsc\} \]
という「同値類 \([a] \; (a \in G)\) を要素とする集合」だ。その \([a]\), \([b]\) の１つ１つは「\(a\) と \(\equiv\) で合同な \(G\) の要素全体」で、その形は
\[ [a] = \{a, a’, \dotsc\} \quad (a, a’, \dotsc \in G) \]
といった \(G\) の部分集合（※ 群とは限らない）である。一方 \((G/N)/(M/N)\) は
\[ (G/N)/(M/N) = \{\langle x\rangle, \langle y\rangle, \dotsc\} \]
という「同値類 \(\langle x\rangle \; (x \in G/N)\) を要素とする集合」。この同値類 \(\langle x\rangle\) は「\(x\) と \(\sim\) で合同な \(G/N\) の要素全体」であるから、その形は
\[ \langle x\rangle = \{ [p], [q], \dotsc, \} \quad ([p], [q], \dotsc \in
G/N) \]
という「\([p]\) の形の同値類を要素とする集合」になっており、\(\langle x\rangle\), \(\langle y\rangle\) の１つ１つは \(G/N\) の部分集合になっている。
\[
\begin{array}{c|c|c}
& G/N & (G/N)/(M/N) \\
\hline
\text{集合の形} & \{[a], [b], \dotsc\} & \{\langle x\rangle, \langle
y\rangle, \dotsc\} \\
\text{要素の形} & [a] & \langle x\rangle \quad (= \langle[p]\rangle) \\
\text{要素は何の部分集合？} & G & G/N \\
\text{要素はどんな集合？} & [a] = \{a, b, \dotsc\}
& \langle x\rangle =\{[p], [q], \dotsc\} \\
& \text{（$a$と$\equiv$で合同な要素全体）} & \text{（$[p]$と$\sim$で合同な要素全体）}
\end{array}
\]
また、正規部分群を \(N=\{e=n_{1}, n_{2}, n_{3}, \dotsc\}\) とするとき、同値類 \([a]\) は「\(a\) に \(N\) の要素１つ１つをかけたものの集合」で
\[ [a] = \{a=an_{1}, an_{2}, an_{3}, \dots\} \]
と書けた。今、\(M=\{e=m_{1}, m_{2}, m_{3}, \dots\}\) とすれば、今度の正規部分群は \(M/N = \{[e]=[m_{1}], [m_{2}], [m_{3}], \dots\}\) だから、新しい同値類は
\begin{align*}
\langle x\rangle = \langle [p]\rangle &= \{[p]=[p][m_{1}], [p][m_{2}],
[p][m_{3}], \dotsc\} \\
&= \{[p] = [pm_{1}], [pm_{2}], [pm_{3}], \dotsc\}
\end{align*}
のようになることに注意しておく。

【第４段階】

さて、仮定により \(M\) もまた \(G\) の正規部分群なので、\(M\) による合同式や同値類というものも新たに考えることができる。「またかよ！」と思う方も多いだろう。実際、３種類もの異なる合同式・同値類をいちいち区別して的確に使い分けるのは困難なので、ここでは \(G\) を \(M\) による同値類で分類・分割した商群 \(G/M\) のイメージ図だけを掲げておく。

さて、これを見て「何かに似ている」と感じなかっただろうか。そう、さっきの \((G/N)/(M/N)\) とよく似た雰囲気の図ではないか？

これを見ると、いよいよ定理の最終目標だった \((G/N)/(M/N) \cong G/M\) のイメージが何となく湧いてきたのではないだろうか。そう、この図が示唆する類似性は単なるイメージではなく、「群として同型」という完全な１対１対応がつけられるのである。これが、本記事冒頭で掲げた定理の意味するところなのだ。

では、この対応関係を証明するために、もう少し詳しく見てみよう。まず、これらは似ているからと言って、イコールで結べるわけではない。実際、図で、左右それぞれの色塗り部 \(M/N\), \(M\) の関係は、
\begin{align*}
M/N &= \{[e], [a], [b]\} \\
M &= [e]\cup [a]\cup [b]
\end{align*}
だ。どちらも重なりのない同値類 \([e]\), \([a]\), \([b]\) を「材料」に作られてはいるが、その作られ方が異なっている。まずは、同様の関係が と にも成立することを示そう。

これは、【第３段階】の最後に触れたことを使うとわかりやすい。今の例では \(M/N = \{[m_{1}], [m_{2}], [m_{3}], \dotsc,\} = \{[e], [a], [b]\}\) としていたから、\((G/N)/(M/N)\) の要素は
\[ \langle[p]\rangle = \{[p], [pa], [pb]\} \]
という形に書けるわけだが、この右辺に現れる３つの要素の和集合は
\begin{equation}
\label{eq:26-5}
[p] \cup [pa] \cup [pb]
\end{equation}
となって、これは \(G/M\) の元である。なぜならば、例えば \([pa]\) だったら
\[ [pa] = \{pa=pan_{1}, pan_{2}, pan_{3}, \dotsc\} \]
となっていて、これは \(p\) を \([a]=\{a=an_{1}, an_{2}, an_{3}, \dotsc\}\) の１つ１つの要素にかけた集合であり、同様のことを考えれば\eqref{eq:26-5}は「\(p\) を \(M=[e] \cup [a]\cup [b]\) の１つ１つの要素にかけた集合」になっているからだ。

以上から、
\begin{align*}
&= \{[p], [pa], [pb]\} \\
&= [p] \cup [pa] \cup [pb]
\end{align*}
のように書け、両者の間に対応関係が作れることがわかる。

最後に、このようにして作られた
\begin{equation}
\label{eq:26-6}
\{[p], [pa], [pb]\} \leftrightarrow [p] \cup [pa] \cup [pb]
\end{equation}
という対応が、群の同型写像になっていることを確かめれば一件落着である。

【第５段階】

\eqref{eq:26-6}が群の同型写像になっていることを示すには、次の３つを確かめればよい。
(a) 準同型になっている。
(b) 全射になっている。
(c) 単射になっている。
まず、(b) の全射になっていることはよい。\((G/N)/(M/N)\) の要素はすべて \(\{[p], [pa], [pb]\}\) の形に書けるし、\(G/M\) の要素はすべて \([p] \cup [pa] \cup [pb]\) の形に表せるからだ。

続いて、(a) の準同型になっていることを確かめよう。\((G/N)/(M/N)\) の２つの要素 \(\{[p], [pa], [pb]\}\), \(\{[q], [qa], [qb]\}\) の積を、それぞれの代表元 \([p]\), \([q]\) の積を通じて計算すると
\[ [p][q] = [pq] \]
だから、求める積は \([pq]\) を代表元とする同値類
\begin{equation}
\label{eq:26-7}
\{[pq], [pqa], [pqb]\}
\end{equation}
である。

一方、\(G/M\) の対応する２つの要素 \([p] \cup [pa] \cup [pb]\), \([q]\cup [qa] \cup [qb]\) の積を求めてみると、今度の代表元は \(p\), \(q\) が取れるから、求める積は \(pq\) を代表元とする同値類
\begin{equation}
\label{eq:26-8}
[pq] \cup [pqa] \cup [pqb]
\end{equation}
である。

\eqref{eq:26-7}, \eqref{eq:26-8}は見事に\eqref{eq:26-6}によって対応しているので、確かに準同型性もなりたつ。

最後に、(c) の単射の確認だが、準同型性が示されたので、これは「単位元に対応するのが単位元だけ」を示せば十分。よって、

\(\{[p], [pa], [pb]\} = M/N\) となるのは \([p]\cup [pa] \cup [pb] = M\) のときだけ

を示せばよいが、この仮定がなりたつなら
\[ \{[p], [pa], [pb]\} = \{[e], [a], [b]\} \]
なので、
\[ [p]\cup [pa] \cup [pb] = [e] \cup [a] \cup [b] = M \]
となって示された。\(\square\)

途中からは合同式はほとんど影をひそめて、もっぱら同値類ばかりが幅を利かせる話になってしまった。この辺りは「合同式で理解する〜」というタイトルにやや偽りありになってしまったことをおわびする。これは私の見通しが甘かったせいで、期待して読まれた方には申し訳ない。