前回の続きである。「群の合同式」を用いた同型定理の証明に移ろう。群論で「同型定理」と言われる定理はいくつかあるが、ここで料理するのは次の定理である。なお、この記事では群演算の記号「\(\star\)」は省略し、単に積として書き並べる。
【定理】 \(G\) を群、\(H\) を \(G\) の部分群、\(N\) を \(G\) の正規部分群とすると、\(H \cap N\) は \(H\) の正規部分群であり、\(H/(H \cap N) \cong (HN)/N\)
\(HN\) が \(G\) の部分群になることと、\(N\) がその正規部分群になることの証明は省略するが、これも合同式の考え方を使ってすっきり解決できる。以下と結構重なる部分もあるので、興味のある方は考えてみるといいだろう（別に難しくはない）。
【証明】 まず、\(N\) が正規部分群なので、\(G\) に合同式「\(\equiv\)」が定義でき、\(G\) が図のように同値類 \([a]\) に分類・分割できる。前回の図と同様、同値類は横長の箱 
で表され、その各々が「合同な要素どうしの集まり」になっている。
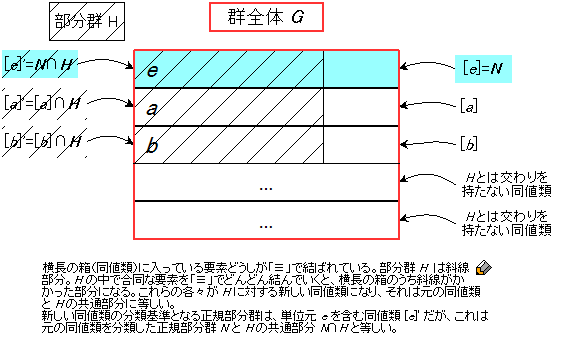
この合同式「\(\equiv\)」を使って、群 \(H\)（図では斜線部で表されている）も同値類に分類・分割してみよう。この図では横長の箱 が合同な要素の集まりになっているので、\(H\) の中だけで合同な要素を「\(\equiv\)」でどんどん結んでいくと、元々の箱 のうち斜線がかかった部分 
ができる。
この斜線付きの箱 の各々が \(H\) を \(\equiv\) で分類した新しい同値類である。これらは、元の同値類と区別するために \(‘\) を付けて \([a]’\) のように表すとしよう。図より、\(a \in H\)のとき
\[ [a]’ \subset [a], \quad [a]’= [a] \cap H \]
は明らかだろう。つまり、斜線付きの箱 \([a]’\) は、斜線なしの箱 \([a]\) の「\(H\) の外にはみ出した部分を削ぎ落としたもの」になっている（なお、\(a \not\in H\) のときは \([a]’\) は定義されない（できない））。
新しい同値類による \(H\) の分類・分割も、ちゃんと \(H\) の正規部分群によってなされていることは容易に確認できる。なぜなら、合同関係 \(\equiv\) は \(H\) が登場するより前から正規部分群 \(N\) によって定義されており、「\(\equiv\) を等号と同じように扱える」という関係
\[
\begin{array}{rrcl}
& a &\equiv& b \\
\star )& c &\equiv& d \\
\hline
& a c &\equiv& b d
\end{array}
\]
は新しい同値類 \([a]’\) を使うかどうかとは無関係に成立するからだ。このため、斜線付きの箱でも代表元の選び方によらず積の属する同値類が決まって、
\[ [a]’ [b]’ = [ab]’ \]
がなりたつ。よって、合同関係 \(\equiv\) は \(G\) だけでなく \(H\) に対してもちゃんとその正規部分群による合同を定めている。その「\(H\) に対する正規部分群」とは「単位元 \(e\) と \(H\) の中で合同な要素全体」、つまり
\[ [e]’ = [e] \cap H = N \cap H \]
である。すなわち、
\(G\) の正規部分群 \(N\) から、部分群 \(H\) の外にはみ出した部分を削り落とした \(N \cap H\) が、\(H\) の \(\equiv\) に関する正規部分群になっている
というわけである。
したがって、この場合の商群
\[ \text{異なる同値類 $[a]’$ 全体の集まり $\{[a]’, [b]’, \dotsc\}$} \]
は \(H/(H \cap N)\) と表される集合である。
さて、図のように、斜線なしの箱は一般には \(H\) と共通部分を持たないものもある。よって、斜線付きの箱から斜線なしの箱へは自然な対応 \([a]’ \mapsto [a]\) が必ずつくのと違って、斜線なしの箱から斜線ありの箱への自然な対応は存在しないこともある。このため、\(H\) の商群 \(H/(H \cap N)\) と \(G\) の商群
\[ G/N = \{[a], [b], \dots\} \]
の間には自然な１対１の対応関係はつかない（つくとは限らない）。
とは言え、写像 \([a]’ \mapsto [a]\) は単射になることは図からすぐわかるし、その上 \([a]'[b]’ = [ab]’\) より準同型写像になっている（積をとってから写しても、写してから積をとっても同じ）ので、その値域は \(H/(H \cap N)\) と同型な群である。ではその値域とはどんな集合だろうか。
図の例では、今考えている値域は
\begin{equation}
\label{eq:25-1}
\{[e], [a], [b]\}
\end{equation}
である。なぜなら、斜線付きの箱から自然な対応がつく斜線なしの箱の全体が \([e]\), \([a]\), \([b]\) の３つだからだ。これは、３つの斜線なし箱を合併した大きな箱 \([e] \cup [a] \cup [b]\) を \(\equiv\) によって漏れもダブリもなく分類し尽くしたものだから、値域\eqref{eq:25-1}は「\(([e] \cup [a] \cup [b])/N\)」と表せる。
一般には、「大きな箱」は \([a] \; (a \in H)\) すべての合併になるので、
\[ \bigcup_{a \in H}[a] = \bigcup_{a \in H} \{an \mid n \in N\} = \{an \mid
a \in H, n \in N\} = HN \]
である。よって、求める値域とは \((HN)/N\) にほかならない。
以上により \(H/(H \cap N) \cong (HN)/N\) がなりたつ。\(\square\)
コメントを残す