\(\newcommand{\field}[1]{\mathbb{#1}}
\newcommand{\Z}{\field{Z}}
\)
群について学ぶとき、正規部分群は避けては通れないものだ。しかし、群論の大抵の解説や教科書的なものでの正規部分群の定義・説明は大変解りにくいものになっている、と私は感じる。それは、正規部分群の「標準的な定義」をそのまま定義として採用してしまっているからだ。標準的な定義というのはこうだ。
群 \(G\) の部分群 \(H\) が
\[ \forall h \in H, \forall g\in G,\quad ghg^{-1} \in H \]
をみたすとき、\(H\) は \(G\) の正規部分群であるという。
あるいは、次の形を取ることもよくある。
群 \(G\) の部分群 \(H\) が
\[ \forall g\in G,\quad gH=Hg \]
をみたすとき、\(H\) は \(G\) の正規部分群であるという。
しかしこんな書き方をされても、初めて正規部分群というものに接する人にとっては何が何やらさっぱりわからない。単なる「部分群」だったら非常に明快でわかりやすい概念だったのに、頭に「正規」がついた途端にさっぱりイメージの湧かない、意味不明なシロモノになってしまって大変にギャップが大きい。
もちろん、気の利いた文献ではその意味・意義というものを、具体例を交えて色々と説明してくれるし、その記述が十分上手で程なく読者が「正規部分群」というものの意義やイメージを的確に掴めるようになるものもあるのだが、しかしそういう書き方をするのなら、何も標準的な定義から入る必要はないのではないか。そうやって紙数を十分に費やす余裕があるのなら、まずは、正規部分群の意義が感じられるような舞台設定や道具立てを、豊富な具体例とともに準備しておき、その後定義に入ればよい。定義も、別に標準的な定義に縛られる必要はなく、用意した舞台や道具立てに沿った形で行っておき、後から「実は標準的な定義はこうなっていて、それと我々の定義はこれこれこのように一致する」という話をすれば十分だ。その方が、読者にとっても書き手にとってもずっと幸せになれるはずだ。
もちろん、標準的な定義にも「色々と準備を必要とせず、最小限の材料だけで到達できる簡潔な定義になっている」というメリットはある。「結局、正規部分群とは何なのか」のエッセンスを追究し、余分なものを削ぎ落とした結果がこのような形にまとめられているので、「必要最小限まで絞ると、たったこれだけで本質を表現できる」ということを味わう上では優れた定義だ。しかしそういう長所を長所として捉えることができるのは、正規部分群というものについて既に十分な運用経験を積んだ人に限った話であって、これが「初学者に最初に与える定義」として適しているかと言えばやはり否だろう。
それで、私が以前から思っているのは、「正規部分群の定義に先だって、まず群というものに『合同式』の類似品を導入することから始めるととてもわかりやすいのではないか」ということだ。整数の合同式の初歩的な知識を前提とする話にはなってしまうが、既に知っている人も多いはずのわかりやすい概念だし、知らない人でもそこら中に解説が転がっており習得するのも容易なはずなので、そのことは大きなハードルにはならないはず、というのが私の見通しだ。
「群に対する合同式もどき」には、副産物もある。群を学習するとあの「同型定理」が出てきて、これの証明がまた無味乾燥で理解するのに一苦労なのだが、合同式もどきを使うと、そこがグッと捉えやすくなるのだ。
というわけで、以下ではその企みに基づいて「合同式の知識を持つ読者に対する、正規部分群の定義と簡単な応用」を書いてみようと思う。(と言うか、同様の先行事例は間違いなく存在するはずで、それに比べれば私の解説など大して出来のよくない模造品に過ぎないだろうが、それでも群論の入り口で苦労している方の助けに少しでもなれば、と思いこうやって公開しておく)
まず、合同式の基本的な性質を軽く復習しよう。例として、ここでは \(\text{mod } 5\) での合同式を考える。合同式の最も重要な特徴は、合同式どうしを足したり、引いたり、かけたりすることができる、ということだ。つまり、和・差・積については「\(\equiv\)」を等号と同じように扱って、以下のように計算することが可能だ。
\begin{align}
&
\begin{array}{rrcl}
& a &\equiv& b \pmod{5} \\
+)& c &\equiv& d \pmod{5} \\
\hline
& a+c &\equiv& b+d \pmod{5}
\end{array}
\quad
\begin{array}{rrcl}
& a &\equiv& b \pmod{5} \\
-)& c &\equiv& d \pmod{5} \\
\hline
& a-c &\equiv& b-d \pmod{5}
\end{array} \notag\\
&
\begin{array}{rrcl}
& a &\equiv& b \pmod{5} \\
\times)& c &\equiv& d \pmod{5} \\
\hline
& a\times c &\equiv& b\times d \pmod{5}
\end{array}
\label{eq:24-1}
\end{align}
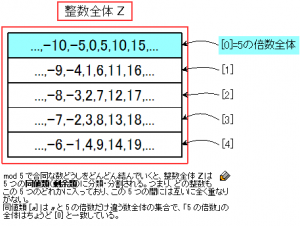
もう1つ重要なポイントは、「同値類による分類」だ。\(\text{mod } 5\) で合同な整数どうしをどんどん「\(\equiv\)」で結んでいくと、次のようになる。
\begin{align*}
\dots \equiv -10 \equiv -5 &\equiv 0 \equiv 5 \equiv 10 \equiv 15 \equiv
\cdots \pmod{5} \\
\dots \equiv -9 \equiv -4 &\equiv 1 \equiv 6 \equiv 11 \equiv 16 \equiv
\cdots \pmod{5} \\
\dots \equiv -8 \equiv -3 &\equiv 2 \equiv 7 \equiv 12 \equiv 17 \equiv
\cdots \pmod{5} \\
\dots \equiv -7 \equiv -2 &\equiv 3 \equiv 8 \equiv 13 \equiv 18 \equiv
\cdots \pmod{5} \\
\dots \equiv -6\equiv -1 &\equiv 4 \equiv 9 \equiv 14 \equiv 19 \equiv
\cdots \pmod{5}
\end{align*}
つまり、整数全体 \(\Z\) は互いに合同な数からなる \(5\) つのグループに分かれる(ここでグループと言っているのは、日常用語のカタカナ言葉としての「グループ」であって、数学用語の「群(group)」ではない。念のため)。
ここで、\(a\) と \(\text{mod } 5\) で合同な整数全体の集合を \([a]\) と書くことにする。例えば
\[ [0] = \{0, \pm 5, \pm 10, \pm 15, \dots \} \]
であり、これは \([5]\) や \([10]\) などと書いても同じ集合である。すると、上の式から、次のような集合の等式が得られる。
\begin{align*}
\dots = [-10] = [-5] = [0] &= [5] = [10] = [15] = \dots \\
\dots = [-9] = [-4] = [1] &= [6] = [11] = [16] = \dots \\
\dots = [-8] = [-3] = [2] &= [7] = [12] = [17] = \dots \\
\dots = [-7] = [-2] = [3] &= [8] = [13] = [18] = \dots \\
\dots = [-6] = [-1] = [4] &= [9] = [14] = [19] = \dots
\end{align*}
\([a]\) は「\(a\) と \(5\) の倍数だけ違う数すべての集合」になっていて、このような集合たちで、全集合 \(\Z\) が漏れもダブリもなく分類し尽くせているわけだ。こうやって分類した5つの集合 \([0], [1], [2], [3], [4]\) の各々を「\(\text{mod } 5\) による \(\Z\) の同値類」とか「剰余類」と言ったりする。「同値類」や「剰余類」というのは、このように「\(a\) と〜だけ違う要素すべての集合」たちによって全体集合が漏れもダブリもなく分類し尽くせるときに使う言葉だ、と思っておけばよい。
すると、上の合同式の性質から、次のようなことがわかる。「\(\pmod{5}\)」は省略している。
\begin{equation}
\label{eq:24-2}
\begin{array}{rrcll}
& 16 &\equiv& 1 & \leftarrow\text{$[1]$ に属するどの数と、} \\
+)& 28 &\equiv& 3 & \leftarrow\text{$[3]$ に属するどの数を足しても、} \\
\hline
& 16+28 &\equiv& 1+3 & \leftarrow\text{結果は合同、つまり両方 $[1+3]$ に属する。}
\end{array}
\end{equation}
今は足し算を例にとったが、当然引き算・掛け算に対しても同様のことがなりたつ。つまり、一般に、こういうことになる。
\begin{align*}
(\text{$[a]$に属する数}) + (\text{$[b]$に属する数}) &\equiv
(\text{$[a+b]$ に属する数}) \\
(\text{$[a]$に属する数}) – (\text{$[b]$に属する数}) &\equiv
(\text{$[a-b]$ に属する数}) \\
(\text{$[a]$に属する数}) \times (\text{$[b]$に属する数}) &\equiv
(\text{$[a\times b]$ に属する数})
\end{align*}
やはり、「\(\pmod{5}\)」は省略している。
このことから、何が読み取れるだろうか。色々あると思うが、ここでは
和・差・積を同値類どうしの演算に自然に拡張できる
ということに着目する。上の例だったら、同値類 \([1]\) と \([3]\) の間の「足し算」というものを、\([1] + [3] = [1+3]\) のようにして定義できる、ということだ。
このように、和・差・積を同値類どうしの間の演算に拡張する上で重要なのが、\eqref{eq:24-2}の性質だ。同値類 \([1]\) は \([16]\) と同じで、\([3]\) は \([28]\) と同じなのだから、\([1]+[3]\) を \([16]+[28]\) として計算したときに、結果が食い違ってしまってはまずい。\eqref{eq:24-2}は、食い違いは起きない(和の定義を矛盾が起きないように拡張できる)ということを意味している。\([1]+[3]\) を \([16]+[28]\) として計算しようが、\([-4]+[283]\) として計算しようが、結果の同値類は
\[ [1 + 3] = [16 + 28] = [-4 + 283] \]
ですべて同じで、食い違いは生じないのだ。
ピンとこない人は、別の例として、\([2] + [4]\) についても \([22] + [9]\) として計算しようが、\([-8]+[124]\) として計算しようが、結果の同値類は同じになることを確かめてみるといいだろう。これは偶然ではなく、合同式の基本性質\eqref{eq:24-1}による必然である。
差や積も同様で、
\begin{align*}
[a] \pm [b] &= [a \pm b] \\
[a] \times [b] &= [a \times b]
\end{align*}
のようにして和・差・積を同値類 \([a]\), \([b]\) どうしの間の演算に拡張できる(これも、ピンとこない人は簡単な値について実例をいくつか作って確かめてみることを勧める)。
このことは、こう言い換えることもできる。同値類の和 \([a] + [b]\) を計算したいときは、\([a]\), \([b]\) から好きな元を1つずつ選び \(x \in [a]\), \(y \in [b]\) とし、\(x+y\) を求めれば \([x+y]\) が \([a]+[b]\) の答になっている、ということである。この \(x\), \(y\) を \([a]\), \([b]\) の代表元という。つまり、差・積も含めて言えば
同値類の和・差・積は、それぞれの任意の代表元による和・差・積から自然に定まる
ということであり、「代表元の選び方の任意性によって結果に破綻が起きない」ということを保証するのが合同式の基本性質\eqref{eq:24-1}ということになる。
さて。ここからようやく群の出番になる。今の話は全整数 \(\Z\) の上での話だったが、類似の話が群 \(G\) の上でできないか考えてみよう。やりたいことは、
\(G\) の上にうまく「合同式」というものを定めて、集合どうし(同値類どうし)の演算が可能になるようにしたい
ということである。それには、\(G\) の上で\eqref{eq:24-1}と同様の性質がなりたっていればよい。つまり、群演算を \(\star\) で表すと、目指すは次の関係式である。
\begin{equation}
\begin{array}{rrcl}
& a &\equiv& b \\
\star)& c &\equiv& d \\
\hline
& a\star c &\equiv& b \star d
\end{array}
\label{eq:24-3}
\end{equation}
(整数 \(\Z\) は和と積という2種類の演算を持っていたが、一般にただの群 \(G\) は演算は \(\star\) 1種類しか持たないので、\eqref{eq:24-1}と類似の式は\eqref{eq:24-3}1つだけになることに注意)\eqref{eq:24-3}のように、「演算 \(\star\) に関しては、\(\equiv\) を等号と同じように使ってよい」ようになっていれば、代表元の選び方を変えても演算 \(\star\) の結果が変わらず、演算 \(\star\) を同値類どうしの間に自然に拡張できる。
\(G\) で\eqref{eq:24-3}をどうやって成立させるのかのプランは、2段階に分けて進めて行く。第1段階では、細かいことは後回しにして、素朴なアイディアに基づいて \(G\) の上で「合同式」を定義してみる。第2段階で、その素朴なアイディアだけでは\eqref{eq:24-3}が成立するには不十分なことがわかって、どういう制約を追加するとうまく行くのかが判明する。
【第1段階】
\(\text{mod } 5\) での整数の合同式では、「\(\equiv\)」は「\(5\) の倍数だけ違う数を結ぶ記号」だった。これを手がかりにして、群 \(G\) でも「〜だけ違う要素を結ぶ記号」という形で「\(\equiv\)」を定めよう。群の場合、「\(5\) の倍数」に当たるものとしては、素朴には「部分群」が使えそうだ。つまり、部分群を1つ固定しておいて、\(G\) の中でその部分群だけ違う要素どうしを「\(\equiv\)」で結ぶ…ということをしてみる。
式で書くと次のようになる。
群の合同式・暫定お気軽版
群 \(G\) の部分群 \(N\) を1つ固定する。「\(a = b \star (\text{$N$ の要素})\)」であるときに、「\(a \equiv b\)」と書く
\(\text{mod } 5\) での整数の合同式では「\(a=b + (\text{$5$ の倍数})\)」の時に「\(a \equiv b\)」と書いたことを真似たわけだ。当然、\(N\) としてどの部分群を採用するか、によって、「\(\equiv\)」の定義も異なってくる。部分群の選択ごとに異なる合同式が定まる、というわけである。
以下の議論で利用しやすいように、
\begin{equation}
\label{eq:24-4}
a \equiv b \Leftrightarrow \exists n \in N, a = b \star n
\end{equation}
が言えることに注意しておく。
【第2段階】
上で注意した通り、今の「暫定版定義」ではまだ不十分だ。それは、これだけでは\eqref{eq:24-3}が成立する保証がないからだが、そのことを今から詳しく説明する。話の順序としては、一旦はそのことを知らないつもりになって、まずは\eqref{eq:24-3}が示せるかどうかを検討する、というスタンスで話を始める。するとそれがうまく行かないことがわかるのだが、その詳しい事情がわかってくると、同時に「ならばどういう条件を付加するとうまく行くようになるのか」がわかってくる、という寸法だ。
ではまず、上の暫定的定義で
\begin{align}
\label{eq:24-5}
a &\equiv b \\
\label{eq:24-6}
c &\equiv d
\end{align}
がなりたっていると仮定しよう。そして、\eqref{eq:24-5},\eqref{eq:24-6}から
\begin{equation}
\label{eq:24-7}
a \star c \equiv b \star d
\end{equation}
を導くことを試みる。
\eqref{eq:24-5}\eqref{eq:24-6}から、\eqref{eq:24-4}によって \(a = b \star n\), \(c = d \star n’ \quad (n, n’ \in N)\) とおける。当面の目標が\eqref{eq:24-7}なので、\eqref{eq:24-4}を念頭に置いて次の式変形を目指そう。
\begin{equation}
\label{eq:24-8}
a \star c = \dots = \dots = (b \star d) \star (\text{$N$ の要素})
\end{equation}
\eqref{eq:24-8}の左辺から計算を始めると
\begin{align}
a \star c &= (b \star n) \star (d \star n’) \notag\\
\label{eq:24-9}
&= b \star n \star d \star n’ \\
&= \text{さて、どうするか…?} \notag
\end{align}
となる。ここで、もしも \(G\) が可換群だったら \(n\) と \(d\) の順番を入れ替えて、\eqref{eq:24-9}に続けて
\begin{align*}
&= b \star d \star n \star n’ \\
&= (b \star d) \star (\underbrace{n \star n’}_{\text{$N$が
群なので$N$の要素}})
\end{align*}
と式変形が進んで目論見通り\eqref{eq:24-8}が示せるのだが、一般には \(G\) は非可換なのでそうは行かない。
以上から、今の合同式の定義では\eqref{eq:24-3}がうまく出てこないことがわかった。しかし、今の計算はまったくの無駄ではない。\eqref{eq:24-8}が目標なら、\(d\) と \(n\) が可換である必要は必ずしもなくて、それらの順番をひっくり返すとき、
\begin{equation}
\label{eq:24-10}
n \star d = d \star n” \quad (\text{ただし、$n” \in N$})
\end{equation}
という変形が起きていれば実の所十分なのである!
この式の意味をちょっと説明しておく。左辺で \(d\) を先頭に持ってくるために順番をひっくり返したいのであるが、そういう強引なことをすると \(n\) が後ろに回るとき、右辺では別の要素 \(n”\) に変わってしまう。しかし、その \(n”\) は \(N\) の中には留まっている、というのが\eqref{eq:24-10}の意味である。
\eqref{eq:24-10}が、可換群の場合の \(n \star d = d \star n\) の拡張になっていることは明白だろう。もちろん、非可換群の場合は\eqref{eq:24-10}は単に \(N\) が部分群であるというだけでは成立しない。一部の特殊な部分群 \(N\) に対してのみ、\eqref{eq:24-10}のような都合のいい等式が成立する。一方、可換群ではすべての部分群がこの特殊な条件をみたす。
実際、\eqref{eq:24-10}がなりたつとき、\eqref{eq:24-9}は次のように変形を続行でき、\(G\) が可換だった場合と同様に\eqref{eq:24-8}が出てくる。
\begin{align*}
&= b \star (n \star d) \star n’ \\
&= b \star (d \star n”) \star n’ \\
&= b \star d \star n” \star n’ \\
&= (b \star d) \star (\underbrace{n” \star n’}_{\text{$N$が群なので$N$の要素}})
\end{align*}
以上のことをまとめると、次のことがわかる。
\(N\) は、\eqref{eq:24-10}をみたすような特殊な部分群とする。つまり、任意の \(n \in N\) と任意の \(d \in G\) に対して、\eqref{eq:24-10}となる \(n”\) が \(N\) 中に存在する。このとき、\eqref{eq:24-3}が成立する
言い換えると、
\(G\) の要素を固定して、部分群 \(N\) の要素との演算順序を入れ替えるとき、後者の変化が \(N\) の中に留まるなら、演算 \(\star\) に関しては \(\equiv\) を等号のように扱ってよい
ということになる。
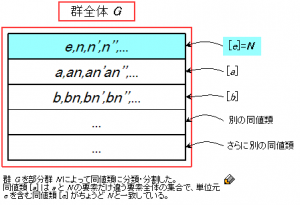
上でも注意した通り、非可換群ではこんなことがなりたつ \(N\) は一部の特殊な部分群に限られる。そして、そのような特殊な部分群を正規部分群と呼ぶのだ。これこそが、標準的な定義では謎に包まれた「正規部分群」の正体である。これは、\eqref{eq:24-3}の成立のために要求される資格なのだ。つまり、\(a\) と合同な要素すべての集合を \([a]\) と書くとき、
\[ [a] \star [b] = [a \star b] \]
のように同値類どうしの演算を定義できるような部分群が正規部分群なのである。
したがって、「群の合同式」の正式な定義は次のようになる。
群の合同式・正式版
群 \(G\) の正規部分群 \(N\) を1つ固定する。「\(a = b \star (\text{$N$ の要素})\)」であるときに、「\(a \equiv b\)」と書く。
\(N\) が正規部分群であることから、演算 \(\star\) は「\(\equiv\)」による同値類どうしに自然に拡張でき、
\[ [a] \star [b] = [a \star b] \]
がなりたつ。
「正規部分群とは何なのか?」について、補足しておこう。\eqref{eq:24-10}を、ちょっと形を変えて再掲する。
\begin{equation}
\label{eq:24-11}
n \star g = g \star n’ \quad (n, n’ \in N, g \in G)
\end{equation}
もし \(n=n’\) ならこの式は \(n\) と \(g\) が可換だ、ということを表すが、たとえ \(n \ne n’\) であっても、\(n\), \(n’\) は「共に \(N\) の元」という意味では「大差ない(\(n \fallingdotseq n’\))」と見なすことができる。この見方では、
\eqref{eq:24-11}の意味は
\(n\) と \(g\) の演算の順序をひっくり返しても、\(n\) は大して大きく変化しない
ということになる。これは、\(n\) は \(g\) と「準可換」だと言い表すことができるだろう(※ 「準可換」というのは正式な用語ではなく、ここだけの用語)。つまり、「演算順序逆転の影響が限定的」であることを「準可換」と呼んでいるわけだ。
もちろん、「演算順序逆転の影響が皆無」である場合が「可換」だから、「準可換」というのは「可換」に類似した「よい性質」であると言える。すなわち、正規部分群とは
「準可換」というよい性質を、\(G\) のすべての要素に対し持っているような要素からなる部分群
と言い表すことができる。つまり、正規部分群とは「たとえ群が非可換であっても、その中に可換性の香りを帯びた構造を構築できるような素材」であり、そのご利益が「\(\equiv\) を等号のように扱うことができる」という形で現れているわけだ。
この流れの中に位置づければ、この記事の最初の方で「正規部分群の標準的な定義の1つ」として引用した「\(\forall g\in G, gH = Hg\)」の意義は明白だろう。結局これは、\eqref{eq:24-11}を \(H=N\) として書き直した式で、正規部分群と可換性の関わりを表現する形の1つになっており(「部分群 \(H\) が、集合として任意の \(g\) と可換」と言っている)、それは「\(\star\) を同値類どうしの演算に拡張できる」という有用性の裏付けがあるからこそ着目に値する性質になっているのだ。
なお、\(\text{mod } 5\) による整数の合同式では \([0]=\text{$5$の倍数全体}\) だったのと同様、正規部分群 \(N\) による群の合同式では \([e]=N\) がなりたつ(\(e\) は単位元)。\([e]\) というのは、「\(e\) と \(N\) の要素だけ異なるもの全体」のことだから、これは当然。
さて、同値類 \([a]\) の各々を1つの「モノ」と見て演算 \(\star\) の対象とする視点が得られたので、そういった「モノ」を要素とする集合
\begin{equation}
\label{eq:24-12}
\{[a], [b], \dotsc \}
\end{equation}
を考えるのは自然な発想だろう。この\eqref{eq:24-12}は群になることが確かめられる。詳しい計算は省略するが、同値類の演算が代表元の演算より自然に定まることから容易に示すことができ、特に単位元は \([e]=N\)、\([a]\) の逆元は \([a]^{-1}=[a^{-1}]\) となっている。各自確かめよ(なお、同値類全体の集合\eqref{eq:24-12}と群 \(G\) を混同しないように注意。整数の合同式の場合だと、\eqref{eq:24-12}に相当するものは「\(5\) で割った余りで整数全体 \(\Z\) を分類した
\[ \{[0], [1], [2], [3], [4]\} \]
という \(5\) つの同値類からなる集合」であって、これは \(\Z\) そのものとは異なる。同値類 \([0], \dots, [4]\) の要素をすべて列挙したものが \(\Z\) に一致するが、「同値類のそれぞれを要素とする集合」は \(\Z\) とは別のものである。
\begin{gather*}
[0] \cup [1] \cup [2] \cup [3] \cup [4] = \Z, \\
\{[0], [1], [2], [3], [4]\} \ne \Z
\end{gather*}
それと同様に、\eqref{eq:24-12}の同値類の要素すべてを列挙したものは \(G\) になるが、だからと言って\eqref{eq:24-12}と \(G\) はイコールにはならない。
\begin{gather*}
[a] \cup [b] \cup \dots = \bigcup_{a \in G} [a] = G\\
\{[a], [b], \dotsc \} = \{[a] \mid a \in G\} \ne G
\end{gather*}
)。
この、演算 \(\star\) によって群になった集合\eqref{eq:24-12}を商群といい、\(G/N\) と書く。
\[ G/N = \{[a], [b], \dotsc \} \]
商群 \(G/N\) とは、正規部分群 \(N\) の要素の違いを無視して \(G\) の要素を同一視したときに現れる群であり、その「\(N\) の違いを同一視している」という所が「\(/N\)」という割り算を意味する表記に表れている。なお、正規部分群\(N\) の取り方を変えると、それに応じて商群 \(G/N\) も当然変わる。
終わりに、我々の正規部分群の定義が、標準的な定義と一致することを確かめておこう。まず、\(N\) が我々の正規部分群だとすると\eqref{eq:24-11}がなりたつので、両辺に左から \(g^{-1}\) を演算すると
\begin{gather*}
g^{-1} \star n \star g = n’ \\
\therefore g^{-1} \star n \star g \in N
\end{gather*}
である。\(g\) は任意だったので、\(g\) を \(g^{-1}\) に置き換えてもよく、
\[ g \star n \star g^{-1} \in N \]
も言える。したがって、我々の正規部分群は、標準的な定義での正規部分群になっていることが確かめられた。
逆に、\(N\) が標準的な定義での正規部分群だとしよう。すると \(g \in G\), \(n \in N\) に対して \(g \star n \star g^{-1} \in N\) だが、\(g\) は任意だったので \(g\) を \(g^{-1}\) に置き換えてもよい。よって
\begin{gather*}
g^{-1} \star n \star g \in N \\
\therefore g^{-1} \star n \star g = n’
\end{gather*}
とおける(ただし、\(n’ \in N\))。両辺に左から \(g\) を演算すると
\[ n \star g = g \star n’ \]
で、\eqref{eq:24-11}が得られた。よって、標準的な定義での正規部分群は、我々の定義での正規部分群にもなっている。
コメントを残す