色玉の個数の期待値と確率

■ 出発点

以下のようなよくある問題を考えてみよう。

箱 A には赤玉が $2$ 個、箱 B には白玉が $3$ 個入っている。A の玉 $1$ 個と B の玉 $1$ 個を無作為に選んで交換する操作を繰り返す。

この操作を $n$ 回を行った後、A の中にある赤玉の個数を $X_{n}$ とする。$X_{n}$ の期待値 $E_{n}=E(X_{n})$ を求めよ。

$n$ 回目の操作で、箱 A から赤玉を取り出す確率 $P_{n}$ を求めよ。

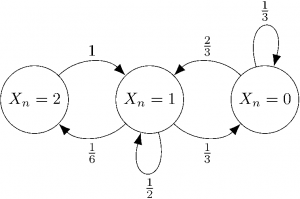
別に捻ったところはなく、平凡な発想で解決する。$X_{n}$ のとりうる値は $2$, $1$, $0$ のどれかしかないから、それぞれの確率を $p_{n}$, $q_{n}$, $r_{n}$ とおけば漸化式が立てられる。遷移図はこうだ（遷移図を導く過程は省略した）。

これより、漸化式はこうなる。
\begin{equation}
\label{eq:expectation-value-4}
\begin{cases}
p_{n+1} &= \frac{1}{6} q_{n} \\
q_{n+1} &= p_{n} + \frac{1}{2} q_{n} + \frac{2}{3}r_{n} \\
r_{n+1} &= \frac{1}{3} q_{n} + \frac{1}{3}r_{n}
\end{cases}
\end{equation}
これは情報量としてはやや余剰がある式になっていて、常に $p_{n}+q_{n}+r_{n}=1$ がなりたつ（これは上の漸化式からもすぐ導ける）ことを使って $r_{n}$ を消去すると
\begin{equation}
\label{eq:expectation-value-5}
\begin{cases}
p_{n+1} &= \frac{1}{6} q_{n} \\
q_{n+1} &= \frac{1}{3} p_{n} – \frac{1}{6}q_{n} + \frac{2}{3}
\end{cases}
\end{equation}
と $\{p_{n}\}, \{q_{n}\}$ のみの漸化式に帰着できる。

求めたい期待値は
\begin{equation}
\label{eq:expectation-value-1}
E_{n}=2p_{n}+q_{n}
\end{equation}
と表せるので、\eqref{eq:expectation-value-5}を使えば
\begin{align}
E_{n+1} &= \frac{1}{3}p_{n} + \frac{1}{6}q_{n} + \frac{2}{3} \notag\\
\label{eq:expectation-value-6}
&= \frac{1}{6}E_{n} + \frac{2}{3}
\end{align}
となって $\{E_{n}\}$ の漸化式が得られる。

また、
\begin{align}
\label{eq:expectation-value-7}
P_{n} &= p_{n-1} \cdot 1 + q_{n-1} \cdot \frac{1}{2} \\
\label{eq:expectation-value-2}
&= \frac{1}{2}(2p_{n-1}+q_{n-1})
\end{align}
なので、上の変形がほぼそのまま使えて
\[ P_{n+1} = \frac{1}{6}P_{n} + \frac{1}{3} \]
という $\{P_{n}\}$ の漸化式が得られる。

こうやって得られた漸化式を解けば問題文の要求通り $E_{n}$ や $P_{n}$ の一般項が求まるが、実は今回の記事の本題はそこではないので、その過程は省略する。

▼ 確率と期待値の関係

さて、\eqref{eq:expectation-value-1}と\eqref{eq:expectation-value-2}を見比べると
\begin{equation}
\label{eq:expectation-value-3}
P_{n+1} = \frac{E_{n}}{2}
\end{equation}
がなりたつことがわかるが、これは次のような自然な考え方とマッチしている: 操作を $n$ 回行った後、箱 A は平均すると $2$ 個中 $E_{n}$ 個の赤玉が入っているので、その比 $\dfrac{E_{n}}{2}$ は次の $n+1$ 回目の操作で赤玉を取り出す確率 $P_{n+1}$ に概ね一致するはずだ。

実際には「概ね」どころか「正確に」一致していたわけだが、これは本問だけでたまたまなりたっているわけではなく、一般になりたつ関係であることが以下のように示せる（東京出版「大学への数学」増刊「解法の探求・確率」の発展編・「期待値の漸化式」のページで、発案者の古川さんの名前とともに紹介されている考え方）。$N$ 個の球が入っている箱の中で、赤玉が $k$ 個である確率を $p(k)$ とすると
\begin{equation}
\begin{split}
\text{《$1$ 個取り出した玉が赤玉である確率》} &= \sum_{k=0}^{N} p(k)
\times \frac{k}{N} = \frac{1}{N} \sum_{k=0}^{N}
k\cdot p(k) \\
&= \frac{\text{《箱の中の赤玉の個数の期待値》}}{N}
\end{split}
\label{eq:expectation-value-26}
\end{equation}
となるわけだ。\eqref{eq:expectation-value-1}と\eqref{eq:expectation-value-7}を見比べれば、この 2 式がまさしく\eqref{eq:expectation-value-26}の関係によって\eqref{eq:expectation-value-3}を生み出していることがわかるだろう。同様に考えることにより、$n$ 回目に B から取り出す玉が赤玉である確率を $Q_{n}$ とすると、
\begin{equation}
\label{eq:expectation-value-15}
Q_{n+1} = \frac{2-E_{n}}{3}
\end{equation}
であることも導ける（赤玉の全個数は $2$ 個で一定なので、A に $X_{n}$ 個あるとき B には $2-X_{n}$ 個。よってその期待値は $E(2-X_{n})=2-E_{n}$）。

さて、改めて基本確率 $p_{n}$, $q_{n}$, $r_{n}$ の漸化式\eqref{eq:expectation-value-4}, \eqref{eq:expectation-value-5}と期待値の式\eqref{eq:expectation-value-1}を見比べると、ちょっと気になることがないだろうか。$E_{n}$ は $p_{n}$, $q_{n}$ の１次結合で表されているわけだが、実は一般の１次結合ではこんなにうまく話は進まない。例えば $F_{n} = p_{n}+q_{n}$ としてみると、\eqref{eq:expectation-value-5}から
\begin{align*}
F_{n+1} &= p_{n+1} + q_{n+1} \\
&= \frac{1}{3} p_{n} + \frac{2}{3}
\end{align*}
となって、\eqref{eq:expectation-value-6}と違ってこの右辺は $F_{n}$ だけを使って表すことはできない。

$E_{n}$ の場合に漸化式\eqref{eq:expectation-value-6}がうまく作れたのは、$p_{n}$, $q_{n}$ の係数が「たまたま」$2$, $1$ という絶妙な値だったおかげなのだ。

この「たまたま」さについてはまた後でじっくり論じることにして、先にこの $2$, $1$ という特殊な値の、数式上の由来を確かめておく。これは基本確率の漸化式\eqref{eq:expectation-value-5}を行列形に書き直してみるとわかりやすい。
\begin{equation}
\label{eq:expectation-value-8}
\begin{pmatrix}
p_{n+1} \\ q_{n+1}
\end{pmatrix} =
\begin{pmatrix}
0 & \frac{1}{6} \\
\frac{1}{3} & -\frac{1}{6}
\end{pmatrix}
\begin{pmatrix}
p_{n} \\ q_{n}
\end{pmatrix} +
\begin{pmatrix}
0 \\ \frac{2}{3}
\end{pmatrix}
\end{equation}
この右辺の係数行列 $
\Bigl(\begin{smallmatrix}
0 & 1/6 \\ 1/3 & -1/6
\end{smallmatrix}\Bigr)
$ は $(2,1)$ を横固有ベクトル（左固有ベクトル・行固有ベクトル）に持っており、このことが $2$, $1$ という数値の特殊性につながっている。\eqref{eq:expectation-value-8}の両辺に左から $(2,1)$ をかければ\eqref{eq:expectation-value-6}が得られ、$(2,1)$ の固有値 $\dfrac{1}{6}$ がそのまま\eqref{eq:expectation-value-6}右辺の $E_{n}$ の係数になっていることも直ちにわかる。

さらに、もう一組の横固有ベクトル・固有値 $(1,-1)$、$-\dfrac{1}{3}$ についても同様の関係がなりたち、$F_{n}’=p_{n}-q_{n}$ とおけば、
\[ F_{n+1}’ = -\frac{1}{3} F_{n}’ – \frac{2}{3} \]
となることも一目瞭然だ。

これらの固有値・固有ベクトルと、元々の確率漸化式\eqref{eq:expectation-value-4}の右辺の係数行列
\[
\begin{pmatrix}
0 & \frac{1}{6} & 0 \\
1 & \frac{1}{2} & \frac{2}{3} \\
0 & \frac{1}{3} & \frac{1}{3}
\end{pmatrix}
\]
にもきれいな関係があるが、たぶんその辺はマルコフ連鎖の教科書にはしっかり書いてあると思うのでここでは踏み込まない（教科書には全然目を通してないです、すんません）。

さて、保留していた議論に戻ろう。上では「たまたま」と書いたが、もちろんそこには意味づけができる。意味もなく単に $p_{n}$, $q_{n}$ を足しただけの $F_{n}$ と違って、$E_{n}$ というのは「赤玉の個数の期待値」というちゃんとした意味を持った由緒ある量で、そう考えればそれが「特別な」関係をみたすことは別に不思議でも何でもない。が、この議論はあくまで「別に不思議ではない」という、self consistent であることの確認にとどまっている。もちろんこのように「つじつまが合っている」ことは積極的に評価する意義があることだろうが、一方数学的に絶対の必然がある、という強いことまで言える議論ではない。このため、この方針（＝まず基本確率を設定し、その漸化式\eqref{eq:expectation-value-4}を立式する）でこの問題に臨む場合、着手時点では\eqref{eq:expectation-value-6}のような $E_{n}$ の漸化式がうまく得られるかどうかは、「その見込みは十分ある」とは言え「うまく行ったらもうけもん」の「出たとこ勝負」という側面がある。

そのようなバクチに頼るのではなく、$E_{n}$ の意味を積極的に活用し、漸化式\eqref{eq:expectation-value-6}を直接立式する（$p_{n}$, $q_{n}$, $r_{n}$ といった基本確率を介さずに）ことはできないか？ということを考えてみよう。

▼ 期待値の漸化式の直接導出

$n+1$ 回目の操作で、「A から B に出ていく赤玉の個数」と「B から A に入ってくる赤玉の個数」をそれぞれ $Y$, $Z$ とおこう。$Y$, $Z$ はいずれも確率変数で、値は $0$ か $1$ しかとらない。すると、「$n+1$ 回目の操作での A の赤玉数の増加分」について
\[ X_{n+1} – X_{n} = -Y + Z \]
という等式がなりたつ。この両辺の期待値をとることによって
\begin{align}
E(X_{n+1}) – E(X_{n}) &= -E(Y) + E(Z) \notag\\
\label{eq:expectation-value-12}
\therefore E_{n+1} – E_{n} &= -E(Y) + E(Z)
\end{align}
となって、話は $Y$, $Z$ の期待値を求めることに帰着する。これらが $\{E_{n}\}$ の項で表せれば都合がいい。

$Y$, $Z$ は $0$ か $1$ の値しかとらない確率変数（「数学ガール」乱択アルゴリズム編でインディケータ確率変数と呼ばれているタイプ。この呼び方が一般的なものかどうかまでは不勉強で知りません。すみません）なので、
\begin{align*}
E(Y) &= \text{《$Y=1$となる確率》} \\
E(Z) &= \text{《$Z=1$となる確率》}
\end{align*}
である。ここで、$Y=1$ という事象は「$n+1$ 回目の操作で A から赤玉が取り出される」という事象で、その確率は $P_{n+1}=\dfrac{E_{n}}{2} \; (\because \eqref{eq:expectation-value-26})$。そして $Z=1$ という事象は「$n+1$ 回目の操作で B から赤玉が取り出される」事象で、その確率は $Q_{n+1}=\dfrac{2-E_{n}}{3} \; (\because \eqref{eq:expectation-value-15})$ だから、
\begin{align*}
E(Y) &= P_{n+1} = \frac{E_{n}}{2} \\
E(Z) &= Q_{n+1} = \frac{2-E_{n}}{3}
\end{align*}
である。よって\eqref{eq:expectation-value-12}より
\[ E_{n+1} – E_{n} = -\frac{E_{n}}{2} + \frac{2-E_{n}}{3} \]
となって、目論見通り $\{E_{n}\}$ の漸化式が得られた！実際、これを整理すれば先ほど導いた\eqref{eq:expectation-value-6}が再現される。

◇ 誤った導出

さて、$\{E_{n}\}$ の漸化式の直接立式に当たって、似たような考え方ではあっても次のようにするのは誤りだ。

再度、$n+1$ 回目の操作による A の赤玉数の増加数に着目する。
\begin{equation}
\label{eq:expectation-value-11}
X_{n+1} -X_{n} =
\begin{cases}
+1 & (\text{A から白、B から赤の場合}) \\
-1 & (\text{A から赤、B から白の場合}) \\
0 &(\text{それ以外の場合})
\end{cases}
\end{equation}
\eqref{eq:expectation-value-3}, \eqref{eq:expectation-value-15}によって、$n+1$ 回目の操作で A, B からそれぞれの色の玉を取り出す確率はこうなる。
\begin{equation}
\label{eq:expectation-value-10}
\begin{array}{c|c|c}
& \text{赤} & \text{白} \\
\hline
\text{A から} & \dfrac{E_{n}}{2} & 1-\dfrac{E_{n}}{2} \\
\text{B から} & \dfrac{2-E_{n}}{3} & 1-\dfrac{2-E_{n}}{3} = \dfrac{1+E_{n}}{3}
\end{array}
\end{equation}
そこで\eqref{eq:expectation-value-11}の両辺の期待値をとり、\eqref{eq:expectation-value-10}の値を使うと
\begin{equation}
\label{eq:expectation-value-9}
E_{n+1} – E_{n} = \underbrace{\Bigl( 1-\frac{E_{n}}{2} \Bigr)}_{\text{Aから白の確率}} \cdot \underbrace{\frac{2-E_{n}}{3}}_{\text{Bから赤の確率}} \times (+1) + \underbrace{\frac{E_{n}}{2}}_{\text{Aから赤の確率}} \cdot \underbrace{\frac{1+E_{n}}{3}}_{\text{Bから白の確率}} \times (-1) + \underbrace{0}_{\text{残りの場合は期待値に寄与しない}}
\end{equation}
となる。

\eqref{eq:expectation-value-9}は、整理すると確かに\eqref{eq:expectation-value-6}が出てくる。このため、一見これは正しい考え方にも思える（実は私も最近までそう思ってしまっていた）。

しかし実際には\eqref{eq:expectation-value-9}は立式としては完全に間違っている。「A から赤玉を取り出す事象」と「B から白玉を取り出す事象」は独立ではないから、それらが同時に起きる確率はそれぞれの確率の積にはならない。実際、$p_{n}$, $q_{n}$, $r_{n}$ を使うと
\[
\begin{array}{c|c|c}
\text{A内の赤玉の個数} & \text{B内の白玉の個数} & \text{Aから赤、Bから白の確率} \\
\hline
X_{n}=2 \quad (\text{確率$p_{n}$}) & 3 & 1 \\
X_{n}=1 \quad (\text{確率$q_{n}$}) & 2 & \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3} \\
X_{n}=0 \quad (\text{確率$r_{n}$}) & 1 & 0
\end{array}
\]
となるから、$n+1$ 回目に「A から赤玉を取り出し、B から白球を取り出す確率」は
\[ p_{n} \times 1 + q_{n} \times \frac{1}{3} + r_{n} \times 0 = p_{n} + \frac{1}{3}q_{n} \]
であって、全然\eqref{eq:expectation-value-9}で出てくる
\[ \frac{E_{n}}{2} \cdot \frac{1+E_{n}}{3} = \frac{2p_{n}+q_{n}}{2} \cdot \frac{1+2p_{n}+q_{n}}{3} \]
に等しくならない。つまり、\eqref{eq:expectation-value-9}から正しい結果\eqref{eq:expectation-value-6}が出てくるのは単なる偶然だ。

◇ 別法

なお、基本確率 $p_{n}$, $q_{n}$, $r_{n}$ を介することなく、直接期待値の漸化式を導くことを目的とする場合、他の方針もある。$E_{n}$ は箱 A の初期状態が「赤赤」から出発した場合の期待値だが、初期状態が「赤白」と「白白」から出発した場合の期待値を $E_{n}’$, $E_{n}”$ のようにおくことで、$\{E_{n}\}$, $\{E_{n}’\}$, $\{E_{n}”\}$ の連立漸化式が立てられる。本記事では、この方針には踏み込まない。

■ 他の問題への応用

上で誤った考え方を紹介したが、この「箱の中の玉を交換する」題材は「立式の考え方が間違っていても、結果の式は正しい」という悩ましい現象が起きやすいようだ。既存の文献上でそのような「これではいけない」と警告が出されている例をご紹介し、さらにここでは「どこを修正すると正しい考え方になってちゃんとした立式が可能になるのか」ということを検討した結果をご覧頂こう。

▼ 「解法の探求・確率」より

まずは、やはり「解法の探求・確率」の「期待値の漸化式」のコーナーの例から。ここで使われている例題は次のような設定だ。

箱 A の初期状態は『赤白白』で、B は何回目の操作でも常に赤と白が等確率で取り出される箱。毎回の操作は「A と B から $1$ 個ずつ玉を取り出し、合わせた $2$ 個から一方を（等確率で）選んで A に入れる」というもの。

この場合は、$n$ 回の操作後の A の赤玉数 $X_{n}$ の期待値 $E_{n}=E(X_{n})$ は次のような漸化式をみたす（導出過程は省略）。
\begin{equation}
\label{eq:expectation-value-14}
E_{n+1} = \frac{5}{6}E_{n} + \frac{1}{4}
\end{equation}

また、A から $n$ 回目に赤玉を取り出す確率を $P_{n}$ とすると、やはり\eqref{eq:expectation-value-26}によって $P_{n+1} = \dfrac{E_{n}}{3}$ となる。

◇ トライ1

A から赤玉が取り出された場合を考える。このとき、

A に白玉が戻されるのは「B から白玉が取り出され、合わせた $2$ 個からその白玉が選ばれる」場合で、その確率は $\dfrac{1}{2} \cdot \dfrac{1}{2} =
\dfrac{1}{4}$
A に赤玉が戻されるのは、その余事象で、確率は $1-\dfrac{1}{4} = \dfrac{3}{4}$

なので、こうなる。
\begin{equation}
\label{eq:expectation-value-16}
X_{n+1} =
\begin{cases}
X_{n} – 1 & (\text{Bから白で、その白がAに戻る場合。確率 } \frac{1}{4}) \\
X_{n} & (\text{それ以外の場合。確率 } \frac{3}{4})
\end{cases}
\end{equation}
また、A から白玉が取り出された場合についても同様に考えれば、こうなる。
\begin{equation}
\label{eq:expectation-value-17}
X_{n+1} =
\begin{cases}
X_{n} + 1 & (\text{Bから赤で、その赤がAに戻る場合。確率 } \frac{1}{4}) \\
X_{n} & (\text{それ以外の場合。確率 } \frac{3}{4})
\end{cases}
\end{equation}

\eqref{eq:expectation-value-16}, \eqref{eq:expectation-value-17}を踏まえて次のように $\{E_{n}\}$ の漸化式を立式してみよう。
\begin{align}
E_{n+1} &= P_{n+1} \cdot \text{《Aから赤が出た場合の$X_{n+1}$の期待値》} + (1-P_{n+1}) \cdot \text{《Aから白が出た場合の$X_{n+1}$の期待値》} \notag\\
\label{eq:expectation-value-13}
&= \frac{E_{n}}{3} \biggl\{ \frac{1}{4}(E_{n}-1) + \frac{3}{4}E_{n} \biggr\} + \Bigl( 1 – \frac{E_{n}}{3} \Bigr) \biggl\{ \frac{3}{4}E_{n} +
\frac{1}{4}(E_{n}+1) \biggr\}
\end{align}
これは、整理すると正しい漸化式\eqref{eq:expectation-value-14}が得られる式なのだが、立式としては正しくない。「解法の探求・確率」の当該記事では、\eqref{eq:expectation-value-13}を整理して\eqref{eq:expectation-value-14}を導いた上で、次のようなコメントを付けている。

…となって、結果的に正しい漸化式が得られます。しかし、いつもこのように立式できる根拠はないので、堂々と使ってはいけませんよ。

このコメントはややあいまいで、ちょっと解釈に苦しむ面がある。“いつもこのように立式できる根拠はない”というのは「この問題の場合は根拠がある（ので大丈夫）」という含意があるのかないのか。“堂々と使ってはいけない”というのは、「実際にはこの立式で（常に）正しい結果が得られるが、その理由はちゃんと説明しないといけないので検算用に留めておくべき」という含意があるのかないのか。実は私はここでも長らく思い違いをしていて、このコメントが消極的でいまいち歯切れが悪い理由は「$P_{n+1}=\dfrac{E_{n}}{3}$ が厳密に成立することを古川さんに指摘されるまで把握していなかったからだ」という風に捉えていて、そこさえクリアできれば立式としては正当性があるとばかり思ってしまっていた。しかし実はそうではなかったのだ。

\eqref{eq:expectation-value-13}の第一の誤りは、《Aから赤が出た場合の$X_{n+1}$の期待値》を
\begin{equation}
\label{eq:expectation-value-19}
\frac{1}{4}(E_{n}-1) + \frac{3}{4}E_{n}
\end{equation}
としている所にある。もちろん、《Aから白が出た場合の$X_{n+1}$の期待値》を
\begin{equation}
\label{eq:expectation-value-20}
\frac{3}{4}E_{n} + \frac{1}{4}(E_{n}+1)
\end{equation}
している所も第二の誤りだ。

…と書くと、不審に感じる方もいるかもしれない。\eqref{eq:expectation-value-16}や\eqref{eq:expectation-value-17}を見ると、いかにも\eqref{eq:expectation-value-19}、\eqref{eq:expectation-value-20}は正しそうに感じられるからだ。

しかし、正しくはこうなのだ。《Aから赤が出た場合の$X_{n+1}$の期待値》というのは、「$n+1$ 回目に A から赤玉を引いたという条件のもとでの、条件付き確率に基づいて定まる $X_{n+1}$ の期待値」すなわち「条件付き期待値」だ。これを $E$ ではなく $E’$ という記号で表すと、\eqref{eq:expectation-value-19}に来るべき値は
\begin{align*}
E'(X_{n+1}) &= \frac{1}{4}E'(X_{n}-1) + \frac{3}{4}E'(X_{n}) \quad (\because \eqref{eq:expectation-value-16}) \\
&= \frac{1}{4}(E'(X_{n}) – 1) + \frac{3}{4} E'(X_{n})
\end{align*}
となる。ここで、もし $E'(X_{n}) = E(X_{n}) (=E_{n})$ がなりたつならこれは\eqref{eq:expectation-value-19}になるのだが、$E’$ は条件付き確率で平均をとっているため、そうはならない（単なる確率 $P(X_{n}=k)$ と、条件付き確率 $P_{\square}(X_{n}=k)$ は違う！）。いちばん解りやすいのは $X_{n}=0$ の確率で、「$n+1$ 回目に A から赤玉を引いた」という情報がなければ $P(X_{n}=0)>0$ だが、その情報を前提にすれば「$n$ 回の操作後に A に赤玉が $0$ 個だった」という可能性はなくなってしまい、条件付き確率は $0$ になる。つまり、「$n+1$ 回目に A から赤玉を引いた」という情報の影響で、A は「より赤玉の存在の確かさが高まった」状態にある、ということだ（同書をお持ちの方は、別ページの「くじ引きの公正さ」のコーナーの「問題３」の「解」の後の説明「実は、１番目の人が…」をお読み頂ければ、同じことが書いてあることが解るだろう）。したがって $E'(X_{n}) > E(X_{n})$ となっていて、\eqref{eq:expectation-value-19}は成立しない。

\eqref{eq:expectation-value-20}が成立しない事情もまったく同様で、今度は「$n+1$ 回目に A から白玉を引いた」という情報の影響で、A は「より赤玉の存在の確かさが薄まった」状態にある（例えば $X_{n}=2$ だった、ということはありえない）わけだ。

◇ トライ2

この問題で正しい考え方に基づいて\eqref{eq:expectation-value-14}を直接導くには、最初に取り上げた例題で利用した「A の赤玉の増加数」$X_{n+1}-X_{n}$ に着目するとよい。

今度も、$n+1$ 回目の操作で、A から出ていく赤玉の個数と A に入ってくる赤玉の個数をそれぞれ $Y$, $Z$ とすれば、$X_{n+1}-X_{n}=-Y+Z$ および
\begin{align*}
E(Y) &= \text{《$Y=1$となる確率》} = P_{n+1} \\
E(Z) &= \text{《$Z=1$となる確率》} = P_{n+1} \cdot \frac{3}{4} +(1-P_{n+1}) \cdot \frac{1}{4}
\end{align*}
がなりたつ。したがって
\begin{align}
E(X_{n+1}) – E(X_{n}) &= -E(Y) + E(Z) \notag\\
\therefore E_{n+1} – E_{n} &= -P_{n+1} + P_{n+1} \cdot \frac{3}{4} + ( 1 – P_{n+1} ) \cdot \frac{1}{4} \notag\\
&= P_{n+1} \cdot \frac{-1}{4} + (1 – P_{n+1}) \cdot \frac{1}{4} \notag\\
\label{eq:expectation-value-21}
\therefore E_{n+1} &= E_{n} + \frac{E_{n}}{3}\cdot \frac{-1}{4} + \Bigl( 1-\frac{E_{n}}{3} \Bigr) \cdot \frac{1}{4}
\end{align}
で、これより正しい漸化式\eqref{eq:expectation-value-14}がちゃんと出てくる。

先ほどの間違った立式\eqref{eq:expectation-value-13}と今度の\eqref{eq:expectation-value-21}を見比べると、なぜ\eqref{eq:expectation-value-13}でも結果だけは正しい式が出てきたのかの事情も見えてくる。一般に、「足して $1$ になる」ような重み $t$, $1-t$ を $E_{n} + \text{《数》}$ にかけて足すと
\begin{equation}
\label{eq:expectation-value-22}
t(E_{n}+a) + (1-t)(E_{n}+b) = E_{n} + ta+(1-t)b
\end{equation}
でやはり $E_{n} + \text{《数》}$ の形が出てくるが、この変形を\eqref{eq:expectation-value-13}の右辺の中かっこの中にそれぞれ適用し、さらに全体に適用すると、次のような式変形が得られる。
\begin{align*}
\text{《\eqref{eq:expectation-value-13}右辺》} &= \frac{E_{n}}{3} \Bigl\{ E_{n} + \frac{-1}{4} \Bigr\} + \Bigl( 1 – \frac{E_{n}}{3} \Bigr) \Bigl\{ E_{n} + \frac{1}{4} \Bigr\} \\
&= E_{n} + \frac{E_{n}}{3}\cdot \frac{-1}{4} + \Bigl( 1-\frac{E_{n}}{3} \Bigr) \cdot \frac{1}{4}
\end{align*}
これは\eqref{eq:expectation-value-21}右辺とまったく同一だ。この観測から、\eqref{eq:expectation-value-13}のような誤った立式でも結果だけは正しい式が出てきてしまう事情が次のように見てとれる。\eqref{eq:expectation-value-13}の立式は\eqref{eq:expectation-value-22}の変形を繰り返すと結局 $E_{n}$ が単体で抜き出せる形で出現するパターンしか出てこず、その $E_{n}$ を左辺に移行して $E_{n+1}-E_{n}$ の形にすると、右辺に残される数はちょうど $Y$ や $Z$ を通じて得られる寄与と合致するようになっているのだ。つまり、上で述べた「$E(X_{n})$ と $E'(X_{n})$ の違い」は、\eqref{eq:expectation-value-22}を通じて $E_{n}$ を単体で抜き出すと、正の誤差と負の誤差がちょうど打ち消し合ってぴったり消えるような違いしか生じさせない、ということになる。

▼ 大数連載記事より

もう１つ同系統の例をご覧頂こう。今度は「大学への数学」2016年10月号の青木さんの記事だ。ここでの設定は次の通り。なお、元の問題では玉の色は赤と青だったが、本記事に合わせて赤と白に変えてある。

箱の初期状態は「赤 $5$ 個、白 $2$ 個」で、毎回の操作は「玉を $1$ 個取り出す。それが赤だったら捨てて白玉を箱に戻し、白だったら赤玉か白玉を等確率（$\dfrac{1}{2}$ ずつ）で箱に戻す」となっている。

本質的には先ほどの例題とどこも変わらない問題なので、同じ考え方が通用する。これまでと同様に $X_{n}$, $E_{n}$, $P_{n}$, $Y$, $Z$ を定めると今度は $P_{n+1}= \dfrac{E_{n}}{7}$ で、
\begin{align}
X_{n+1} – X_{n} &= -Y + Z \notag\\
\label{eq:expectation-value-24}
\therefore E_{n+1} – E_{n} &= -E(Y) + E(Z) = -P_{n+1} + (1-P_{n+1})\cdot \frac{1}{2}
\end{align}
となっている。

元記事では、求めるべき量は $E_{n}$ ではなく $P_{n}$ だったのでこれを $\{P_{n}\}$ の漸化式に書き換えればよい。つまり\eqref{eq:expectation-value-24}の両辺を $7$ で割って $n$ を $1$ つずらせば
\[ P_{n+1} = \frac{11}{14}P_{n} + \frac{1}{14} \]
が得られる。後は簡単だ。

◇ 誤った立式

元記事では、\eqref{eq:expectation-value-13}に相当する立式が $\{P_{n}\}$ の方の漸化式で紹介され、次のように戒められている。

『$n$ 回目で赤玉を引くと、赤玉の個数は $1$ 減るから、$n+1$ 回目で赤玉を引く確率は $\dfrac{1}{7}$ 減る。$n$ 回目で白玉を引くと、赤玉の個数は平均すると $\dfrac{1}{2}$ 個増えるので、$n+1$ 回目で赤玉を引く確率は $\dfrac{1}{14}$ だけ増える。よって、
\begin{equation}
\label{eq:expectation-value-23}
P_{n+1} = P_{n} \Bigl( P_{n} – \frac{1}{7} \Bigr) + (1-P_{n}) \Bigl( P_{n} + \frac{1}{14} \Bigr)
\end{equation}
』とするのはいけません。結果的に、\eqref{eq:expectation-value-23}は正しくなりはするのですが、正当性はまったくありません。

\eqref{eq:expectation-value-23}は、両辺を $7$ 倍して $n$ をひとつずらせば
\begin{equation}
\label{eq:expectation-value-18}
E_{n+1} = \frac{E_{n}}{7} (E_{n}-1) + \Bigl( 1 – \frac{E_{n}}{7} \Bigr) \Bigl( E_{n} + \frac{1}{2} \Bigr)
\end{equation}
となって、\eqref{eq:expectation-value-13}に相当する立式であることが見てとれる。

１年ほど前に元記事を最初に見かけた時の私は、まだ\eqref{eq:expectation-value-13}が誤った立式だと理解していなかったため、愚かにも次のような道筋を辿ってしまった。

\eqref{eq:expectation-value-23}の上に書いてある議論は確かに不成立だから、\eqref{eq:expectation-value-23}を直接立式するのは正しくないけれども、\eqref{eq:expectation-value-26}を使って\eqref{eq:expectation-value-18}のように期待値の関係に帰着すれば、\eqref{eq:expectation-value-13}と同様正当化されるだろう、と見当をつける
\eqref{eq:expectation-value-24}のように「$n+1$ 回目の増加分」に着目して期待値の漸化式を立式してみると
\begin{equation}
\label{eq:expectation-value-25}
E_{n+1} = E_{n} + \frac{E_{n}}{7}\cdot (-1) + \Bigl( 1 – \frac{E_{n}}{7} \Bigr) \cdot \frac{1}{2}
\end{equation}
が得られるが、\eqref{eq:expectation-value-18}が\eqref{eq:expectation-value-22}の変形を通じて\eqref{eq:expectation-value-25}と同一の式になっていることを確認
なので\eqref{eq:expectation-value-18}も正当化される、と誤認
以上の考えを青木さんに伝えた所、\eqref{eq:expectation-value-18}も立式としては誤っている、と説明を受けるも、その時点では何がどう誤っているのか理解できず
後でゆっくり考え直した結果、やっとこさ $E$ と $E’$ をごちゃまぜにしていたという重大な誤りに気づく

という体たらくだった。何ともお恥ずかしい次第だ。

▼ ポリアの壷

これまで見てきたことから、「箱の中の玉を交換する」題材では「赤玉の増加数の期待値」$E_{n+1} – E_{n}$ はなかなか有用な量であることがおわかりだろう。この量の優秀さを体感できる例として、最後に有名な「ポリアの壷」をこの技法で解決してみる。

設定はこうだ。

壷の初期状態は赤玉 $a$ 個と白玉 $b$ 個。毎回の操作は、壷から $1$ 個取り出し、取り出した玉に同色の玉を新たに $c$ 個加えて壷に戻す

$n$ 回目に取り出す玉が赤玉である確率 $P_{n}$ を求めることが目標である。

ポリアの壷には様々な解法があるようだが、「大学への数学」2014年4月号の栗田さんの記事の解法が最も優れているのだろう。ここで紹介するものはそれほどの簡明さはないが、見て頂く価値はあると思っている。

これまでと同様に、$n$ 回の操作後の壷の中の赤玉の個数を $X_{n}$、その期待値を $E_{n}=E(X_{n})$ とおく。毎回壷の中の玉の数は $c$ 個ずつ増えていくので、$n$ 回の操作後は玉の総数は $a+b+nc$。すると、やはり\eqref{eq:expectation-value-26}によって $P_{n+1}=\dfrac{E_{n}}{a+b+nc}$ になる。

ここで、「玉の総数 $N$ が一定でないから\eqref{eq:expectation-value-26}は使えないのでは？」と疑問に思う方もいるだろう。尤もな疑問だが、これは大丈夫なのである。「一定でない」とは言っても、$n$ を決めれば $N$ は $N=a+b+nc$ と一意に決まるので、\eqref{eq:expectation-value-26}の過程を再度追ってみれば問題なく成立することがわかるはずだ。（もし、$n$ を決めても $N$ が一意に決まらず、確率的に複数の値をとりうるのであればもはや\eqref{eq:expectation-value-26}は成立しなくなる（実際に、$P_{n}$ や $E_{n}$ を表す式を立ててみればわかる）。しかし $N$ が確率に依存せず、$n$ のみに応じて一意に決まるのであれば、定数である必要はない）

すると、$n+1$ 回目の操作で壷に新たに足される赤玉の個数を $Y$ とすると $X_{n+1} – X_{n} = Y$ で、$Y$ は確率 $P_{n+1}$ で $c$、確率 $1-P_{n+1}$ で $0$ という値をとるから
\begin{align*}
E(X_{n+1}) – E(X_{n}) &= E(Y) = P_{n+1} \times c + (1-P_{n+1}) \times 0 \\
\therefore E_{n+1} – E_{n} &= \frac{E_{n}}{a+b+nc} \times c
\end{align*}
となってこれまで通り漸化式が立つ。これより
\begin{align*}
E_{n+1} &= \frac{a+b+(n+1)c}{a+b+nc}E_{n} \\
\therefore \frac{E_{n+1}}{a+b+(n+1)c} &= \frac{E_{n}}{a+b+nc} = \text{const.} \\
\therefore P_{n} &= P_{1} = \frac{a}{a+b}
\end{align*}
となって、有名な結果 $P_{n}=\dfrac{a}{a+b}$（$n$ によらない定数）が得られる。

◇ オマケ

本記事の趣旨からは外れるが、この「$P_{n}$ が $n$ によらない定数になる」ということは、確率を「濃度」と捉えるとほとんど計算なしで理解できる。壷に赤玉と白玉が入っていて、$1$ 個取り出した時にそれが赤玉である確率が $0.3$、という状況を、「壷には赤と白の色水が交ざって入っていて、赤の濃度が $0.3$」と捉えてみよう。元の設定では $1$ 回の操作で玉が $c$ 個増え、その色は確率 $0.3$ で赤、$0.7$ で白なわけだが、これは「$c$ グラムの色水を壷に足す。その濃度は、赤が $0.3$、白が $0.7$」と解釈できる。すると、元々壷に入っていた色水と同じ濃度の色水を足すので、全体の濃度が変わらないのは当たり前だ。

この「色玉を色水と見なし、確率を濃度と見なす」考え方は、他にも有効な場面はちょくちょくある。本記事で扱った例題を、色水濃度モデルで捉え直すとどうなるか、試してみるのも一興だろう。

投稿日

2017年11月21日

カテゴリー:

数学

投稿者:

井汲景太

タグ: