\(\newcommand{\kumiawase}[2]{{}_{#1}\text{C}_{#2}}\)
東京出版の「解法の探求・確率」に、割と大き目の間違いを見つけたので編集部に手紙でお知らせしたのですが、半年以上経っても未だに正誤表にも「大学への数学」本誌にも訂正が出る様子がなく、返答も特にない(確かに、「知らせる」ことだけが目的だったため返信用の切手や封筒は敢えて省きましたので、返答がないことそれ自体は差し支えないのですが)ので、ここで公開することにします。ですので、この記事は「解法の探求・確率」をお持ちでない方にはよくわからない話になってしまいます。ご了承ください。
「解法の探求・確率」は最初に刊行されてから結構大きな改訂を経ているようですが、当該の記事は私の手元にある旧版と内容はまったく変わっていないようです(書店でざっと見てみた限り。もし新版をお持ちの方が、本記事の記述が不適である部分に気づいたらお知らせ頂けると幸いです)。ですので、この誤りは最初の刊行以来10年以上にわたってずーっと見逃されていたもので、これだけはっきりした誤りがそんなにも長く気づかれないまま放置され続けていたというのはちょっと驚きました。
誤りがあったのは発展編の4「くじ引きの公平さ」(※ 旧版では発展編の3)の問題2です。と言っても、「問題2の解」には誤りはありません。しくじっているのは「解」の後に続く解説部分になります。そこでは
何番目の人についても、\(1\) 番目の人と同じ確率である…☆
と結論づけられていますが、これが誤っています。実際には、「途中の何番目かまでの人は \(1\) 番目の人と同じ確率になるが、それ以降は確率が下がっていく」ということになります。
まずは簡単に検証可能な例として \(n=3\), \(k=1\) の場合をとります。このとき ○××、×○×、××○ の \(3\) 通りの順列が等確率になりますが、このうち前 \(2\) 者では \(1\) 番目の人が当たり、最後の順列では \(2\) 番目にくじを引く人が当たるわけですから、
\[ \text{$1$番目の人が当たる確率} = \frac{2}{3}, \quad \text{$2$番目の人が当たる確率} = \frac{1}{3} \]
で一致しません。\(2\) 人目の方が \(1\) 人目よりも当たる確率が下がります。これで、少なくとも一般の \(n\), \(k\) に対しては☆が成立しないことは明白です。
そこでは☆を数学的帰納法で証明しようとしていますが、一見すると確かに不備はないように見える議論になっています。どこがまずいのか、ですが、\(1\) 番目の人が○を引く確率を \(f(n,k)\) としたとき、
\begin{equation}
\label{eq:kaitan-kakuritsu-1}
f(n,k) = \frac{k(2n-k-1)}{n(n-1)}
\end{equation}
にはならない例外的ケースがあるのが原因です。
そこで述べられている数学的帰納法の考え方だと、\(2\) 番目の人が○を引く確率は、次のように計算されることになります。
\begin{equation}
\begin{split}
& \frac{k}{n} f(n-1,k-1) + \frac{n-k}{n}\cdot \frac{k}{n-1} f(n-2,
k-1)\\
&\quad {}+ \frac{n-k}{n} \cdot \frac{n-1-k}{n-1} f(n-2,k)
\end{split}
\label{eq:kaitan-kakuritsu-2}
\end{equation}
これは、\eqref{eq:kaitan-kakuritsu-1}を機械的に適用して整理していくと確かに \(\frac{k(2n-k-1)}{n(n-1)}\) になります。しかし、その計算には落とし穴があります。
\eqref{eq:kaitan-kakuritsu-2}は「\(n\) の値がより小さいときの \(f\) の値」に帰着して計算している式なので、この計算が想定通りに行くためには \(n\) が小さくなっても\eqref{eq:kaitan-kakuritsu-1}が成立することが必要です。ところが、\eqref{eq:kaitan-kakuritsu-1}は \(n=1\) の場合は明らかに使えない式です。このため、例えば \(n=3\) の場合には\eqref{eq:kaitan-kakuritsu-2}で\eqref{eq:kaitan-kakuritsu-1}を使うことができません。これが、上の \(n=3\), \(k=1\) の例が反例となっている事情です(\(n=3\) の場合、\eqref{eq:kaitan-kakuritsu-1}を機械的に適用したときの計算は、実は分母と分子で \(0\) を約分する箇所があるため有効性を失っている)。
数学的帰納法に先行する「解」の議論に不備はありません。ただしそれは問題文の
\begin{equation}
\label{eq:kaitan-kakuritsu-3}
3 \leqq k \leqq n-5
\end{equation}
という条件のおかげです。\eqref{eq:kaitan-kakuritsu-3}は、「解」中の(A)や(B)に挙がっている順列に、「△」が○になるタイプと×になるタイプの両方が存在することを保証する条件で、そのおかげでその後の議論が滞りなく進行するようになっています。\(u\) 番目の人に対しては、その条件は
\begin{equation}
\label{eq:kaitan-kakuritsu-4}
u \leqq k \leqq n-2u+1
\end{equation}
となりますが、\(n\), \(k\) を固定したまま \(u=3,4,5,\dots\) と \(u\) を増やしていくと、そのうち\eqref{eq:kaitan-kakuritsu-4}が成立しなくなる局面にぶち当たります。
なので、「解」の後の「上のように考えれば、☆である」という主張は正しくなく、正しくは「何番目の人についても、\eqref{eq:kaitan-kakuritsu-4}が成立していれば、\(1\) 番目の人と同じ確率である」ということまでしか言えていないわけです。
ただし、\eqref{eq:kaitan-kakuritsu-4}が成立しなくなったとたんに確率が変化するというわけでもありません。\eqref{eq:kaitan-kakuritsu-4}は十分条件であって必要条件ではないからです。
例えば \(n=10\), \(k=2\) だと\eqref{eq:kaitan-kakuritsu-3}は成立しませんが、この場合も次のようにすれば \(1\) 番目と \(3\) 番目の人が当たる確率が一致することが示せます。この解は、勤め先のとある方(以前、「体とガロア理論」を貸してくださった方)によるものです。
【解】
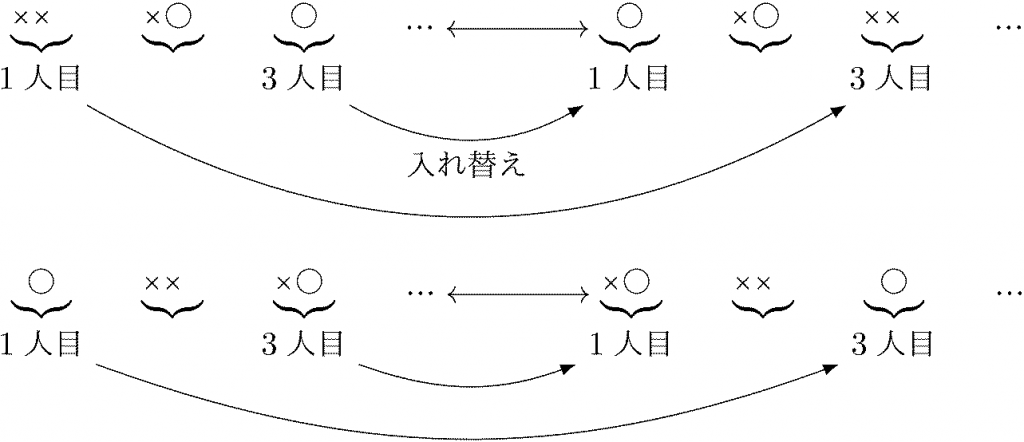
\(\kumiawase{10}{2}=45\) 通りの○ \(2\) 個・× \(8\) 個の順列が等確率で起こるが、これらに対して次のような入れ替えを考える。
この入れ替えで、\(3\) 人目が当たる順列 \(\leftrightarrow\) \(1\) 人目が当たる順列 なる1対1対応が作れるので、順列の個数は同じ。よって確率も同じ。\(\square\)
今の説明だと、やはり何番目に引く人も \(1\) 番目の人と同じ確率になってしまいそうなので、そうならない理由を補足します。今の \(n=10\), \(k=2\) の場合、\(1\) 番目から \(5\) 番目までの人の確率は同じなのですが、\(6\) 番目の人の確率はそれより下がります。なぜならば、例えば
\[ \underbrace{\text{×○}}_{\text{$1$人目}} \underbrace{\text{××}}_{\text{$2$人目}} \underbrace{\text{××}}_{\text{$3$人目}} \underbrace{\text{○}}_{\text{$4$人目}} \underbrace{\text{××}}_{\text{$5$人目}} \underbrace{\text{×}}_{\text{$6$人目}} \]
という順列では \(1\) 人目が当たりますが、これに対しては先ほどと同様な入れ替えで「\(6\) 人目が当たる順列」は作れません。また、
\[ \underbrace{\text{×○}}_{\text{$1$人目}} \underbrace{\text{××}}_{\text{$2$人目}} \underbrace{\text{×○}}_{\text{$3$人目}} \underbrace{\text{××}}_{\text{$4$人目}} \underbrace{\text{××}}_{\text{$5$人目}} \]
という順列でもそうです。
このくじ引きでは、誰が引いても原則として「○」「×○」「××」のいずれかの引き方しかありえないのですが、例外として「最後に \(1\) 本だけ×が残っている」状態で順番が回ってきた人だけ「×」単独という引き方になることがあります。上の \(n=10\), \(k=2\) の例では、\(5\) 人目まではそういう巡り合わせになることはないのですが、\(6\) 人目になるとそういう貧乏くじを引かされるハメになる可能性が出てきます。また、\(6\) 人目は、そもそも自分の番が回ってくる前にすべてのくじが消費され尽くしてしまう可能性もあるわけです。こういった事情により、\(6\) 人目が当たる順列になると、\(1\) 人目が当たる順列との1対1対応がなくなって、前者の方が少なくなります。
一般の \(n\), \(k\) の場合も話はまったく同様で、\(n\), \(k\) によって決まるある定数 \(N\) があって、\(N\) 人目までは \(1\) 人目と同じ確率になるが、それ以降の人は \(1\) 人目より当たる確率が低くなる、というようになるわけです。最初に挙げた \(n=3\), \(k=1\) というのは \(N=1\) になるような例です。
(\(N\) を \(n\), \(k\) の具体的な式として表すのは、○と×のどちらが多いかの場合分けと floor 関数を使えば容易ですが割愛します)
コメントを残す