しばらく前に http://www.geocities.jp/yoimondai/1/essei.html というコーナーを見つけ、「これは面白い」と隙間時間にちょびっとずつ読み進めています。非常に鋭い着眼・解法が次々と繰り出されて、結構な難問も小学生に（！）理解可能な解答がこさえられているのには舌を巻きました。この方だったら、http://6504.teacup.com/aozoram/bbs/3816 で紹介されている「定理」のような問題でも、小学生向けの解答を鮮やかに編み出してしまえるかもしれません（私は高校生向けの解法しか作れないや…）。→そうか、これは１年くらい前の「高校への数学」に \(n=3,5,7\) の場合が載っていて、\(n\) が一般の奇数でも成立するとも書いてありますね。なるほど、トレミーの定理を使えばいいのですね…。→【2017, 6/1 追記】さらに、「大学への数学」の2006年12月号に \(n=3,5\) の場合に「切り貼り」だけで示す巧妙な証明が紹介されてますね…。円周角の定理とその周辺が使ってあるので小学生向けとまでは行きませんが、中学生なら十分理解できます。確かめてはいませんが、そこでの話の進み方からして、一般の奇数 \(n\) に対しても同じ手法で示せそうです。

その一方で、中学受験での算数分野の闇の深さには改めて暗澹たる気分にならざるをえませんでした。代表的な話をいくつか挙げると、まずは三平方の定理や二項係数といった知識を、事実上先取りしていながら形の上では先取りしていない体を装ういびつさが真っ先に挙がります。三平方の定理を使う場面では、それを証明するのと同じ図を自分で書いて計算させる。また、二項係数で求められる場合の数を計算する場合は、１回１回全部格子街路の最短経路数に帰着して、経路数を書き入れて求めさせる。それは確かにそういう解法を見れば、小学生でも「得られた答が正しい」ということはわかるでしょう。しかしそれを小学生が「自力で、何も参照せずに」再現できるように訓練する、ということが果たしていいことなのかどうかは甚だ疑問です。そんな不自然な技能を身につけさせることが子どもにとって「豊かな体験」になるのでしょうか。子どもの発達が然るべき段階に達したところで「三平方の定理」「二項係数とその応用」という形で体系的に、自在に扱えるようにすることの方がよっぽど子どもたちのためになるのではないでしょうか。小学生向けの形を取って教える限り、それは「こういう場面ではこういう図を書いて計算する」「こういう場面ではこういう対応関係を自力で構築し、こういうやり方で経路数に還元する」という知識を、場面ごとに細分化して教え込み、かつそれを素早く引き出せる反復訓練を行う、という「パターンに当てはめて条件反射として瞬時に出てくるようにする」タイプの、非常に不健全なものになるしかないように思います。

と言っても、そのコーナーを書いた方に直接の責任を問うつもりはありません。問題は、「こうすれば小学生にも解ける（から出題してしまおう）」とする中学校の出題者の短慮・無配慮にあるでしょう。そんなことをしたら、教育産業の側が「こういう出題がされる以上、それを体系化して不特定多数が習得可能な『手筋』にまとめなければならない」と反応してしまうのは当然だからです。中学入試の算数分野は、「受験生の発想力の豊かさ」を試すという本来の目的から離れて、出題者と教育産業従事者の間の「知恵比べ」の場になってしまっているようですが、そのあり方は余りに貧しい姿なのではないでしょうか。

それからもうひとつは、「手描きでは簡単には描けないような正確・複雑な図」を前提とした解がやたら頻発することです。立体の断面を考えたり、正方格子・正三角形格子等を補助線として書いてその中に考察対象の図形を埋め込んで処理するタイプの問題・解法で特に顕著ですが、「こうやって切ると（こういう格子を描くと）こういう図になって、これがこうこうこうなっている」という説明は、「他人が書いたものを見て読めば」確かにそうなっている、と納得・理解することは十分可能です。しかし同じことを小学生が試験会場で「自力で、何も参照せず」実行できるかと言うと…。そんなに大量の三角形を、あちこちの長さの辻褄が狂わないようにパパッと描くとか、影になって見えない部分が実際にはどうなっているのかを正確に把握して描くなんてことは高校生どころか大人の私だってそう簡単にはできない（し、時間制限のある試験会場では絶対に１つや２つのミスは避けられない）でしょう。にもかかわらずそれを「小学生にできる技法」として「教える」ためには「こういうタイプの問題では、ここに着目してこういう図を描くとこうなってるんだよ」ということを、やはりかなり細分化してパターン別に暗記させ、「手が勝手に動いて十分正確な図が描ける」「ちゃんとした図を描かずとも、粗い概略図だけで（もしくはそもそも頭の中に思い浮かべるだけで）何がどうなってるのかわかる」ようになるまで徹底的に反復演習させるしかないのではないでしょうか。私には、それは「教育」とは言えない、非常に貧しい「別の何か」にしか思えません。

第３の点は、「キーポイントとなる着眼点・規則性が、途中経過なしでいきなり提示される」ことが頻発することです。本来適切な着眼点というものは色々な試行錯誤を経てようやく見つかるもので、「なぜそこに着目するとうまく行くのか」という理由は、事情がわかってからでないと見えてこないことが多いものです。また、より重要なこととして、鍵となる規則性は「ほんとにそうなっているのかどうか・見落としや思い違いはないのか」という点を検証しない限り「単なる思い込み」と違いはなく、そんなものでたとえ正しい数値が得られたとしてもそれは単なる結果論でしかありません。当てずっぽうがたまたま的中しただけで何の価値もない。これは前段落の話とも通じる部分があって、図を描くとき、例えば「こことこことを結ぶ直線がほんとにちゃんとこの点を通るのかどうか」といった類の考察・検証がすっ飛ばされていきなり（結果だけは）正しい図が提示されていたりします。

いや、そうなってしまう事情は表面的にはよくわかります。小学生だと、試行錯誤するに当たっての技法・方法論の備えがまだ非常に少ないし、検証しようにもやはりそのための手段が全然揃っていない。なので、天下りに結果だけ与える、というやり方しかないのでしょう。また、中学入試の算数では採点対象になるのは原則として結果の数値だけで、途中経過を問われることはほとんどないでしょうからね。しかし、その結果として小学生が訓練させられるのは「とにかく結果だけは正しい式を、ただの推測によって１秒でも早く見つけ出すこと」になってしまい、「教わった手筋を次々当てはめて、ほんの２〜３個の例が当てはまるだけの規則性を、正当性を度外視して使って結果の数値を求める」ということばかりに上達していくのです。その弊害が、中学・高校になって同じように「検証もせず推測に過ぎない式を無条件で正しいと決めつけ、教える側がいくら注意しても直らない」という不毛極まりない事態として現れているのでしょう。以前から憂慮していたことではありますが、その源はやはりこういう所にあったんだな、ということが確認できたように思います。

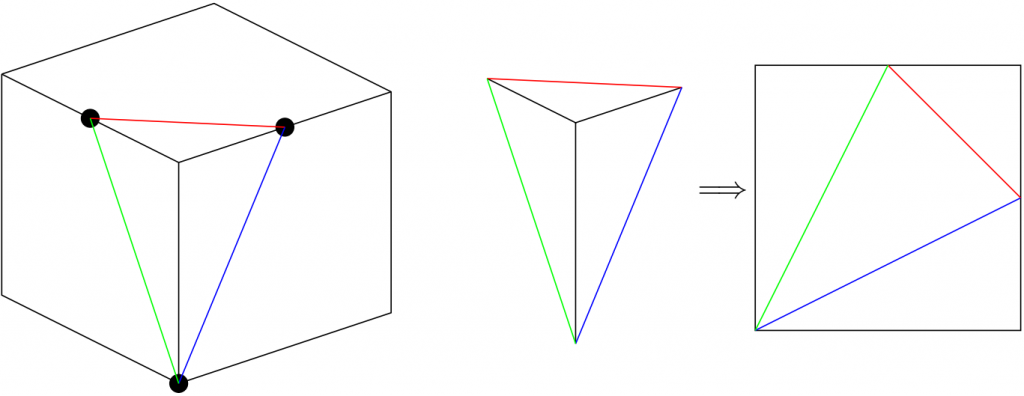
で、私が見た中でも飛び抜けて「こりゃひでえ」と思った（※ 注・後述）のが、立方体のひとつのかどを平面で切って三角錐を作るとき、隣りあう 2 辺のそれぞれの中点と、もう 1 辺の向こう側の頂点を通る平面で切ると、できる三角錐の展開図が正方形になる（図参照）、という知識が「中学入試の常識」的に扱われていることでした。

※ そのコーナーはまだ途中までしか目を通してないので、今後もっとひどいと思う話も出てくるのかもしれませんが、ひとまず現段階まで目を通した中では最悪の部類です。【追記】結局、これよりひどい題材は出てきませんでした。

これ、展開図に広げると重なっていた辺がちょうど180度や90度に開くというのがすごく意外で、「え、本当？」と言いたくなりますよね。その記事には何の説明もなくさも当たり前のことのように書かれていたうえ、さらに記事を読み進めると、切り取るかどの頂点からの距離が 1:1:2 になる場合だけでなく、1:2:3 になるような点を 3 辺上に取りそれらを結ぶ平面で切っても、展開図が正方形に準じる形になる三角錐ができる、という話まで出てきて混乱に拍車をかけます。

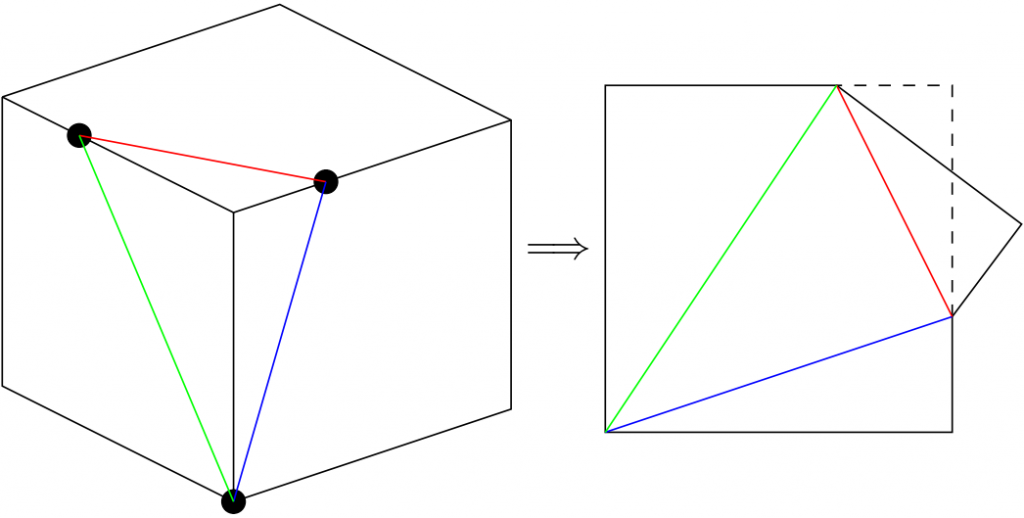
展開図は上の右側の図のように正方形にはならないのですが、その右上部分の直角三角形を赤線で切り取ってクルッと裏返して点線部のように付け直せば正方形になる、と！こっちの図でも、左下隅が90度に開くとか、付け直した点線の方が実線と180度の角度でつながる…というのは全然明らかではありません。

最初私は「え、どういうこと？ひょっとして、立方体（と言うか直方体）のかどを切り落としてできる三角錐の展開図って、切り方によらずここが180度になるようになっていて、それを私が知らなかっただけ？」とかなり混乱してしまいました。

半信半疑ながら本当かどうか確かめてみようと思ったものの、当初私には初等的に確かめる手段が思いつけなかったので、やむなく三角関数の加法定理を使って計算しました。その結果、確かに 1:1:2 や 1:2:3 の場合にきっちりそういう角度になることはわかったのですが、そこの計算の手応えからしても、やはりどうも特別な切り方をした時だけしかなりたたたない性質であるように思える。にもかかわらず、今考えている切り方の場合にはきっちり180度や90度になる理由の、小学生にも理解できる説明がなかなかできなくて参りました。その時私の頭の中で渦巻いていた考えはこうです。「いくらこの性質が正しいとは言っても、小学生に伝える時に天下りで結果だけ与えて『こうなってるから覚えろ』とはしないだろう。小学生に理解できる説明の仕方がない限り、いくら何でも中学入試には出ないはずだ。角錐の体積みたいに、『基本的でありながら厳密な説明は困難なので、教科書にも結果だけ載ってて正当化は省略される』例外とは違って、そういう基本性は全然ない話なんだし」これほど秩序だった形はしていませんでしたが、言語化するならこういう感じのものでした。

だいぶ混乱が続いてからやっと「そうか、逆に正方形の図の方から出発して、上辺と右辺の然るべき分点を取って図の色線を谷折りにすれば、辺の長さが一致することからうまく三角錐が折り上がり、その三角錐は合わさった頂点に集まる 3 つの角が全部直角で、かつ陵の長さが 1:1:2 や 1:2:3 になる、と言えるのか…。これで、元の立方体を題意の切り方をしたときと合同（相似）な三角錐ができるので、確かに小学生でも理解できる証明になるな」と思い当たってやっとこさ解決に至りました。

中学入試の算数というのはこんな知識に基づいて、図の色線の３角形の面積を求めさせたりする問題を出すようなのですが、しかしこれほどまでに特異性の高い知識を「常識」として持っていないといけないというのは余りに不健全に過ぎるように思います。上の話は要するに、「正方形の方から出発してうまく三角錐が組み上がるような特殊な分点を取って作った三角錐になるときだけ、立方体（直方体）のかどを切り取った三角錐の展開図が小学生でも計算可能な題材になる」ということで、「そういう特殊な比（1:1:2 や 1:2:3）とその生かし方を事前に覚えていた場合に限って小学生でも処理できるに過ぎない」ということです。予備知識がない小学生が「立方体や直方体のかどを切り落としたらどうなるか」という観点だけで取り組んでも、絶対これが解けるようにはならないわけです。そんなバカな話があってたまるか、と誰しも力説したくなりませんか、これ？

上で、展開図が正方形になることの説明を思いつくのに手こずったのは、ひとり私のみの無知・知的怠慢に責が帰せられる事項ではないと思います。実際、後日職場の方2名に尋ねてみても、この話というのは初耳という反応で、こんな特異な（中学生・高校生になってもっと汎用性のある手法を自然に身につけたら何の使い道もなくなるような）知識が「常識」として要求されるヤクザな世界なんざまっぴらごめんだ！と意気軒昂に盛り上がったものです。

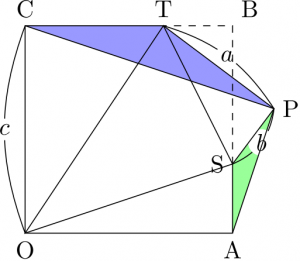
んで、そのとき話した方の一方から、「この性質って結局、比を \(a:b:c\) とするとき \(a+b=c\) ならば一般になりたつってことじゃないですか？最初の図で、いちいち右上の直角三角形を切り離し裏返して付け直す必要がなかったのは、たまたま \(a=b\) になってたからということで」と指摘されて、さらに「展開図から逆に考えて、\(a+b=c\) のときに直方体のかどになるような三角錐が作れるってことは、上の展開図上で \(\text{A}\), \(\text{P}\), \(\text{C}\) から\(\text{OS}\), \(\text{ST}\), \(\text{OT}\) に下ろした垂線が \(1\) 点で交わるってことですね。これを、背景を考えずに平面幾何の定理として捉えると非自明で、そういう強い性質が、\(a+b=c\) という条件だけで一般になりたつってのはちょっと意外で面白い」という指摘も受けました。それをきっかけにこの図について２〜３日間考えてみたところ、（私にとっては）結構面白い結果がイモヅル式に得られたので、指摘してくれた方に毎日進捗を伝えました。彼も割と面白がってくれたので、本記事の残りではそれを紹介していきましょう。ひょっとしたらすでによく知られた有名な話に過ぎず、わざわざ公開するほどの価値はないことかもしれませんが、その場合はコメント欄で優しく教えてください（笑）。

命題1

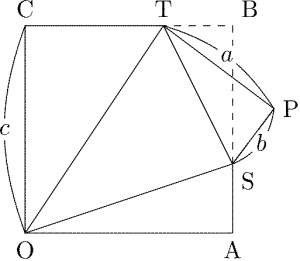
上の図で \(\text{OABC}\) は正方形であり、\(\triangle\text{STP}\) は \(\triangle\text{TSB}\) を \(ST\) で切り離して裏返し、付け直したものとする。また \(a+b=c\) で、したがって \(\text{CT}=a\), \(\text{AS}=b\) もなりたっているとする。このとき、\(\text{A}\), \(\text{P}\), \(\text{C}\) から \(\text{OS}\), \(\text{ST}\), \(\text{OT}\) に下ろした垂線は \(1\) 点で交わる。

証明

（上述の通り4面体の展開図と見れば、4面体が折り上がることから明らかだが、ここではそういうデザルグの定理っぽい「3次元化」を介さず、普通の平面幾何の手続きでの証明を試みる）

ひとつの証明は、O を原点とする座標系を設定し、ベクトルや内積を使ってどんどん成分計算していく、というやり方だろう。私の最初の計算はこれで、先にここからいろんな関係を見つけて「え？なんでこんなことがなりたつの？」と思って幾何的な説明を発見していく、という流れだった。ここではそういう背後の計算は出さずに、幾何的な説明だけをお見せする。

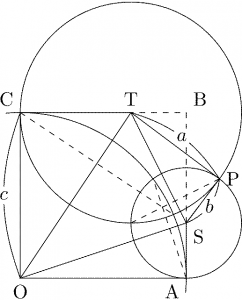
\(\text{T}\), \(\text{S}\) を中心にそれぞれ半径 \(a\), \(b\) の円を書くと \(\text{P}\) ともう 1 点で交わる。よって 2 円の共通弦が \(\text{P}\) から \(\text{ST}\) に下ろした垂線である。

同様に、\(\text{O}\) を中心とする半径 \(c\) の円を描くと、先ほどのそれぞれの円との共通弦が「\(\text{A}\) から \(\text{OS}\) に下ろした垂線」および「\(\text{C}\) から \(\text{OT}\) に下ろした垂線」になる。

よって「平面上の互いに異なる \(3\) 円の \(2\) 円ずつの共通弦は \(1\) 点で交わるか交わらない平行 \(3\) 直線になる」という有名定理（モンジュの定理）によって、\(3\) 垂線は \(1\) 点で交わる（「平行 \(3\) 直線」のケースは、\(\text{O}\), \(\text{S}\), \(\text{T}\) が \(1\) 直線上にないことからありえない）。\(\square\)

命題2

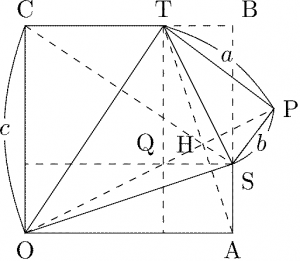
直線 \(\text{OP}\), \(\text{AT}\), \(\text{CS}\) は \(1\) 点で交わり、その交点は命題1の交点と一致する。

証明

命題1の交点を H とする。図のように点 \(\text{Q}\) をとる。つまり、\(\text{Q}\) は \(\text{S}\) を通り \(\text{OA}\) と平行な直線と、\(\text{T}\) を通り \(\text{OC}\) と平行な直線の交点である。すると、\(\text{Q}\) は命題1の \(\text{S, T}\) を中心とする \(2\) 円の交点のうち、\(\text{P}\) ではない方。よってまず \(\text{H}\) は \(\text{PQ}\) 上にあり、さらに
\begin{equation}
\label{eq:square-tenkaizu-1}
\text{PQ} \perp \text{ST}
\end{equation}
である。

また、長方形 \(\text{BSQT}\) を \(90^{\circ}\) 回転すると \(\text{OQ}\) を対角線とする長方形になるので、対応する対角線は直交し
\begin{equation}
\label{eq:square-tenkaizu-2}
\text{OQ} \perp \text{ST}
\end{equation}
もなりたつ。

\eqref{eq:square-tenkaizu-1}, \eqref{eq:square-tenkaizu-2}より \(\text{O, P, Q, H}\) は共線である。

同様にして、\(90^{\circ}\) 回転した長方形の対角線どうしの直交から \(\text{AT} \perp \text{OS}\) および \(\text{CS} \perp \text{OT}\) が言え、それらから \(\text{A, H, T}\) が共線であることと \(\text{C, H, S}\) も共線であることが出る。よって \(\text{OP}\), \(\text{AT}\), \(\text{CS}\) はすべて \(\text{H}\) を通る。\(\square\)

命題3

\(\angle \text{APC}=90^{\circ}\) である。

証明

\(\triangle\text{CTP}\) と \(\triangle\text{ASP}\) を比べると、\(\text{PT} \perp \text{PS}\), \(\text{CT} \perp \text{AS}\) で \(\text{PT}=\text{CT}=a\), \(\text{PS}=\text{AS}=b\) であるから、\(\triangle\text{CTP}\) を \(\text{P}\) を中心に \(90^{\circ}\) 回転し、\(\frac{b}{a}\) 倍にしたものが \(\triangle\text{ASP}\) になっている。よって対応する 2 辺 \(\text{PC}\), \(\text{PA}\) は直交する。\(\square\)

【追記】ここはもっと素朴に、「\(\triangle\text{CTP}\), \(\triangle\text{ASP}\) は共に二等辺三角形で、それぞれの底角の \(2\) 倍が \(\angle\text{PTB}\), \(\angle\text{PSB}\) になっている。が、\(\triangle\text{STB} \equiv \triangle\text{TSP}\) だったから \(\angle\text{PTB} = \angle\text{PSB}\) なので、二等辺三角形の底角も等しい。よって \(\angle\text{APC} = \angle\text{SPT} = 90^{\circ}\)」の方がよかったかもしれない。始めに思いついたのはこっちの方だったものの、後から思いついた「\(90^{\circ}\) 回転」を主軸にした解法の方がスマートに思えてそちらを書いてしまったが、こうやって見比べると結局こっちの方がシンプルでいいようにも思えてきた。

命題3の成立に気づいたのは、次のような経緯だった。命題1は「\(\text{A, C, P}\) から \(\triangle\text{OST}\) の各辺に下ろした垂線が \(1\) 点で交わる」ということを言っているが、するとその双対（※ 注）で「\(\text{O, S, T}\) から \(\triangle\text{ACP}\) の各辺に下ろした垂線が \(1\) 点で交わる」ということも成立することになる。この双対の交点はどこなんだろう？ということを座標で計算してみると、何と \(\text{AC}\) の中点、つまり正方形の中心になった。「これってきっと何か意味があるよな…」と思ってちょっと考えてみると、これらの垂線は線分 \(\text{AC}\), \(\text{AP}\), \(\text{CP}\) の垂直二等分線であることがすぐわかるので、その交点と言ったら \(\triangle\text{ACP}\) の外心である。それが辺 \(\text{AC}\) の中点になるということは、\(\triangle\text{ACP}\) は斜辺が \(\text{AC}\) の直角三角形ということにほかならない。

※ 一般に、\(\triangle\text{ABC}\) と \(\triangle\text{XYZ}\) があるとき、「\(\text{A, B, C}\) から \(\text{YZ, ZX, XY}\) に下ろした垂線の足が \(1\) 点で交わる」ことと「\(\text{X, Y, Z}\) から \(\text{BC, CA, AB}\) に下ろした垂線の足が \(1\) 点で交わる」ことは同値。証明は、内積を使ってちょっと工夫すれば単純計算でできます（東京出版「解法のスーパーテクニック」図形編の定理4.3を使えば中学生でも証明可能）。さらに、今回の話では直接必要としませんが、\(\triangle\text{ABC}\) と \(\triangle\text{XYZ}\) が別々の平面に載っていても自然に拡張した形で成立します。

で、さらに気づいたのが「命題1の証明って、展開図が特殊な形をしている必要はなくて、一般に \(4\) 面体の展開図で通用するんじゃないか？」ということで、まさしくその通りだった。

命題4

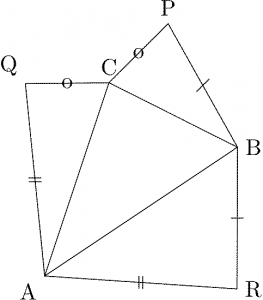
平面上の \(\triangle\text{ABC}\) に対して、\(3\) 点 \(\text{P, Q, R}\) を \(\text{AQ}=\text{AR}\), \(\text{BR}=\text{BP}\), \(\text{CP}=\text{CQ}\) をみたすように取る。このとき、\(\text{P, Q, R}\) から \(\text{BC, CA, AB}\) に下ろした垂線は \(1\) 点で交わる。

証明

命題1と同様に、モンジュの定理で示せる。\(\square\)

この場合も、双対によって \(\text{A,B,C}\) から \(\text{QR, RP, PQ}\) に下ろした垂線は \(1\) 点で交わるが、それらの垂線は \(\text{QR, RP, PQ}\) の垂直二等分線だから、\(1\) 点で交わるのは当たり前（\(\triangle\text{PQR}\) の外心）。そこから逆に、モンジュの定理の通常とは別の証明ができることも気づいた。

モンジュの定理の別証明

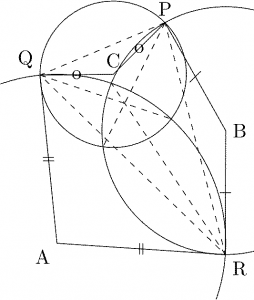
図のように、\(\text{A, B, C}\) を中心とする \(3\) 円が \(\text{P, Q, R}\) で交わっているとする。\(\text{A,B,C}\) から \(\text{QR, RP, PQ}\) に下ろした垂線は \(\text{QR, RP, PQ}\) の垂直二等分線だから \(\triangle\text{PQR}\) の外心で会する（\(\text{P, Q, R}\) が一直線上にある場合は、\(2\) 円の交点の選び方を変えて \(\triangle\text{PQR}\) が潰れないようにしておく）。よってその双対で、\(\text{P, Q,
R}\) から \(\text{BC, CA, AB}\) に下ろした垂線も \(1\) 点で交わる（もしくは互いに平行な \(3\) 直線になる）ので、\(3\) 円の \(2\) 円ずつの共通弦もその \(1\) 点で交わる（もしくは互いに平行で交わらない）。\(\square\)

これは座標も根軸も使わない。かわりに上述の双対性の定理を使っているので、証明としてより初等的になったわけではないが、よそではあんまり見かけない証明にはなっているのではないかと思う。